Газпром 2025
Ошибка.
Попробуйте повторить позже
В трубопроводе цилиндрической формы установлено скребковое устройство вдоль трубы, предназначенное для очистки внутренней
поверхности от парафинистых и смолистых отложений, имеющее форму треугольной призмы. В поперечном сечении трубопровода в виде
круглого циферблата с часовой разметкой, вершины треугольника скребкового устройства находятся в точках окружности на часовых
отметках «1:30», «4:00» и «5:00». Определить диаметр трубопровода, если площадь сечения скребкового устройства 900
мм
Источники:
Подсказка 1
Задача, похоже, геометрическая, значит нам нужен чертёж! Как мы можем использовать зафиксированные на циферблате вершины треугольника?
Подсказка 2
Знание положений вершин по сути даёт нам зафиксированные углы треугольника, а что требуется при это. узнать? Какие теоремы есть, связывающие величины треугольника с окружностью?
Подсказка 3
Нам поможет теорема синусов и формула площади треугольника через радиус описанной окружности! Но что же делать с углами? Это ведь совсем не табличные значения, которые мы все помним...
Подсказка 4
Тут варианты разные: можно работать с двойными углами и попробовать напрямую вытащить все нужные синусы, но... если вы хорошо владеете тригонометрией, и помните формулы преобразования суммы/разности в произведение и наоборот, то в целом всё страшное выражение для площади сводится к табличному синусу!
Построим сечение трубопровода в виде окружности с часовой разметкой. Отметим вершины треугольника (сечения скребкового устройства,
имеющего форму треугольной призмы) и обозначим их соответственно буквами
и
Заметим, что
— вписанный в
окружность. Обозначим радиус этой окружности
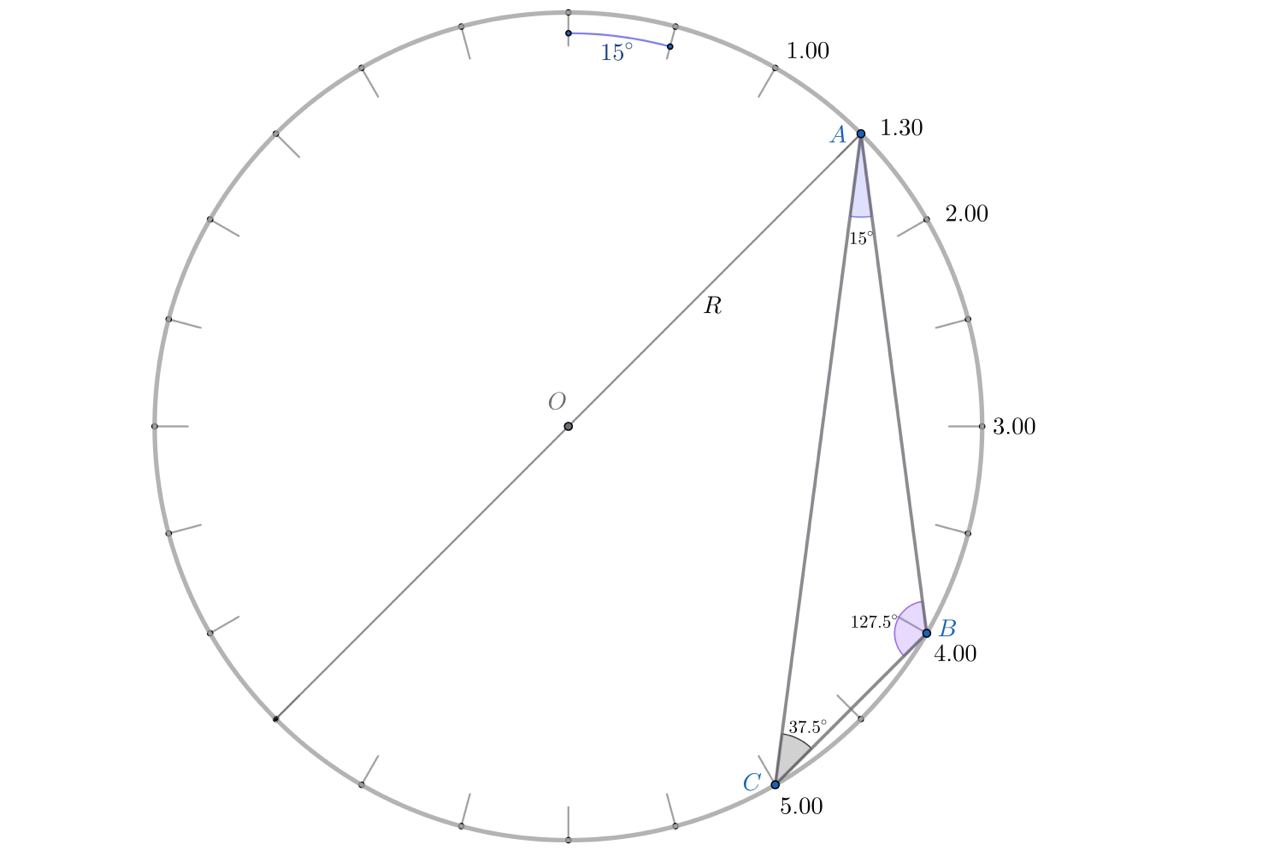
Часовое деление на циферблате соответствует центральному углу Найдем углы
как вписанные углы в
окружность:
Используя формулу для нахождения площади треугольника через радиус описанной окружности и теорему синусов, получим:
Отсюда получаем:
Вычислим:
Так как
то полученное выражение можно преобразовать следующим образом:
Тогда получим:
Тогда следовательно:
Тогда в итоге
120 мм
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




