Регион 2025
Ошибка.
Попробуйте повторить позже
Высоты и
остроугольного треугольника
пересекаются в точке
высоты треугольника
пересекаются в точке
точка
— середина стороны
Докажите, что
Источники:
Подсказка 1:
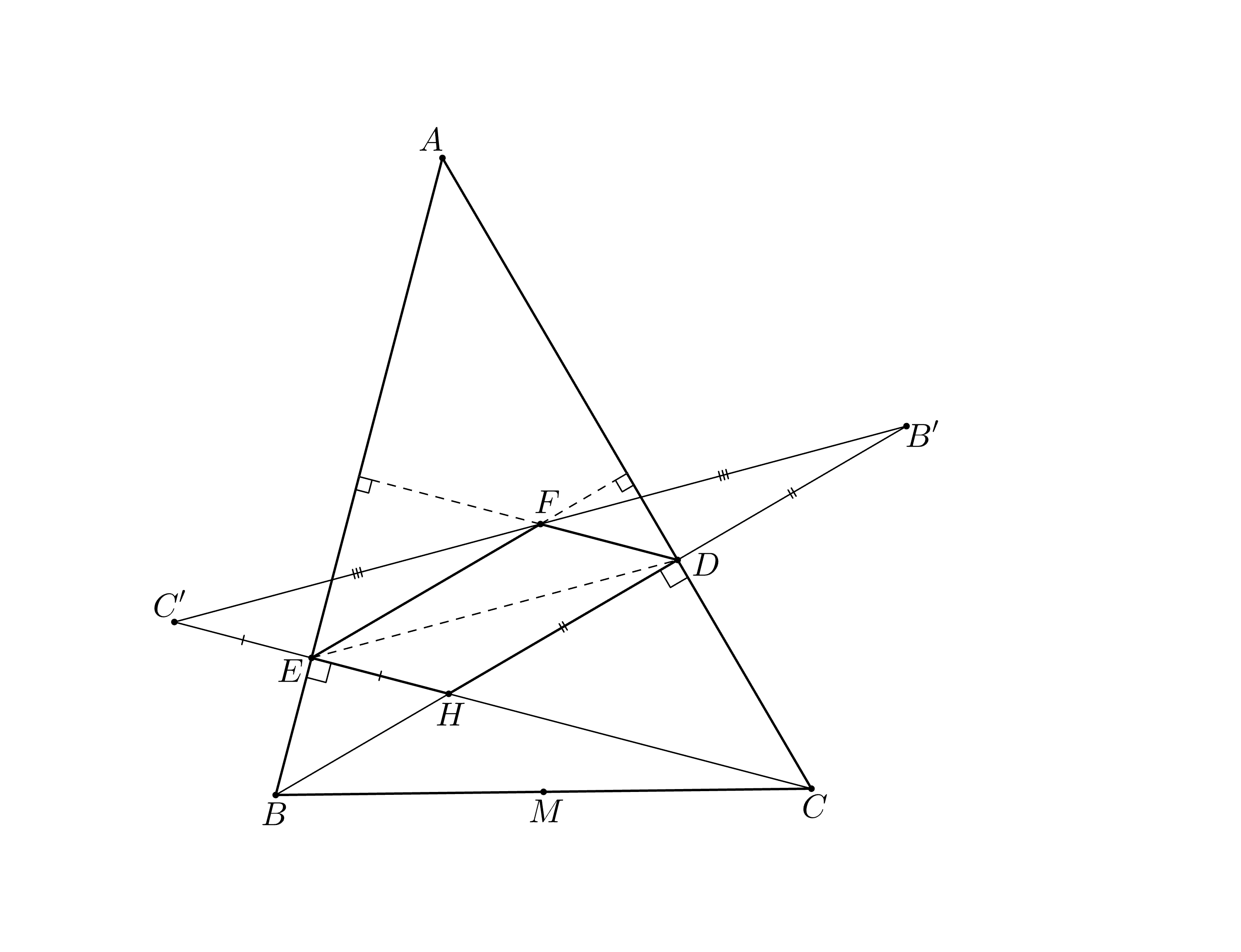
Хорошей идеей будет отражение точки H относительно BA и AC (назовём полученные точки C' и B'). Почему? Потому что BH = BC' и CH = CB' в силу симметрии. Есть ощущение, что новые отрезки проще связать с MF.
Подсказка 2:
Изучите получше чертёж. Поищите пары параллельных прямых. А что можно сказать про точки C', B' и F?
Подсказка 3:
F — середина C'B'. Теперь вернёмся к первой подсказке. Как связать MF с BC' и CB'? Учитывая, что нас просят доказать неравенство, можно попробовать выразить вектор MF через векторы BC' и CB', не забывайте, что M — середина BC.
Отразим относительно
получим точку
лежащую на
и такую, что
— середина
и
Аналогично,
точка
симметричная
относительно
такова, что
— середина
и
Так как имеем
Аналогично
Значит,
— параллелограмм. В треугольнике
точки
и
— середины сторон. Отметим также середину
стороны
тогда
— параллелограмм.
Получается, что
совпадает с
т.е.
— середина
Так как
и
— середины
и
имеем векторное
равенство
Тогда по неравенству треугольника () получаем
что равно
Этим доказано
нужное неравенство.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




