Тема Закл (финал) 10 класс

Закл 2025

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 10 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#126725Максимум баллов за задание: 7

Найдите все натуральные $n,$ для которых существует такое чётное натуральное $a,$ что число

2 n (a− 1)(a − 1)...(a − 1)

является точным квадратом.

Источники: ВСОШ, ЗЭ, 2025, 9.3 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте сначала вручную разобраться с n = 1, 2, 3. Для этих случаев достаточно вспомнить утверждение о том, что если произведение двух взаимно простых чисел — квадрат, то каждое из них также является квадратом. В частности, при n = 3 надо поработать с нодами скобок a - 1, a + 1, a² + a + 1. Быть может, этот ход мыслей можно развить и для больших n?

Подсказка 2:

Итак, скорее всего вы поняли, что n = 1, 2 подойдёт, а n = 3 — нет. Чем остальные случаи отличаются. Например, если n > 3, то оно находится между двумя натуральными степенями двойки. То есть существует такое натуральное k, что 2^k ≤ n < 2^{k + 1}. Подумайте, как это можно использовать.

Подсказка 3:

Если записать скобку a^{2^k} – 1 как (a^{2^{k – 1}} – 1)(a^{2^{k – 1}} + 1), то становится ясно, что все произведение состоит из скобки a^{2^{k – 1}} + 1 и скобок вида a^m – 1. А как насчёт того, чтобы посмотреть на нод выражений a^{2^{k – 1}} + 1 и a^{2^k} – 1 с произвольной скобкой a^m – 1?

Подсказка 4:

Нод второго выражения и a^m – 1 кратен ноду первого выражения и a^m - 1. Чтобы было проще работать, вот вам интересный факт: нод второй скобки и a^m – 1 равен a^нод(2^k, m) – 1. Осталось поработать с нодом 2^k и m.

Подсказка 5:

Исходя из выбора k, ясно, что нод 2^k и m не превышает 2^{k – 1}. Попробуйте теперь показать, что ноды выражений a^{2^{k – 1}} + 1 и a^{2^k} – 1 с a^m – 1 совпадают. Кажется, это раскроет идею подсказки 3.

Подсказка 6:

Стало быть, a^{2^{k – 1}} + 1 — точный квадрат. А вас это не смущает?

Показать ответ и решение

Заметим, что для $n= 1$ подойдёт $a =10.$ Для $n =2$ подойдёт $a= 8.$

Предположим, что для $n =3$ нашлось требуемое число $a.$ Тогда число

2 3 3 2 (a − 1)(a − 1)(a − 1)= (a− 1) (a +1)(a + a+ 1)

является точным квадратом. Поскольку

2 a + a+ 1= a(a+ 1)+1,

числа $a+ 1$ и $a2+ a+ 1$ взаимно просты. Раз число $a+1$ нечётно, числа $a+ 1$ и $a− 1$ также взаимно просты. Следовательно, числа $a+ 1$ и $(a− 1)(a2+a +1)$ — точные квадраты. В частности, число $a+ 1$ при делении на 3 может давать лишь остаток 0 или 1, а тогда число $a− 1$ не делится на 3. Отсюда

2 НО Д(a− 1,a + a+1)= НОД (a − 1,(a +2)(a − 1)+ 3)= НО Д(a − 1,3)=1,

значит, числа $a− 1$ и $a2 +a+ 1$ также являются точными квадратами. Но второе являться квадратом не может, поскольку

a2 < a2 +a+ 1< (a+1)2.

Противоречие.

Осталось доказать, что требуемого $a$ не существует при $n ≥4.$ Предположим, что такое $a$ нашлось. Возьмём такое натуральное $k ≥2,$ что $2k ≤n < 2k+1.$ Поскольку

a2k − 1= (a2k−1 − 1)(a2k−1 + 1),

число

(a− 1)(a2 − 1)...(an− 1)

представляется в виде произведения $2k−1 a +1$ и нескольких множителей вида $m a − 1,$ где $1≤ m ≤n$ и $k m ⁄=2 .$

Докажем, что множитель $2k−1 a +1$ взаимно прост со всеми остальными множителями в этом разложении. Пусть $2k−1 a + 1$ и $am − 1$ имеют некоторый общий делитель $d.$ Тогда и НОД $k a2 − 1$ и $am − 1$ кратен $d.$ Но

k k НОД(a2 − 1,am− 1)= aНОД(2 ,m)− 1.

Поскольку $k m ⁄= 2$ и $k+1 m ≤n < 2 ,$ число $m$ не может делиться на $k 2 .$ Таким образом, $k Н ОД(2,m )$ — степень двойки, не превосходящая $k−1 2 .$ Следовательно, $2k−1 a − 1$ делится на НОД $2k a − 1$ и $m a − 1,$ а, значит, делится и на $d.$ Поскольку $a$ чётно, числа $2k−1 a − 1$ и $2k−1 a + 1$ не имеют общих делителей, отличных от 1, значит, $d= 1,$ что и требовалось.

Множитель $2k−1 a + 1$ взаимно прост со всеми остальными множителями в произведении, являющемся точным квадратом, поэтому он сам является точным квадратом. Тогда $k−1 a2 +1$ и $k−1 a2$ — отличающиеся на 1 квадраты натуральных чисел, что невозможно. Значит, наше предположение неверно, и для $n≥ 4$ требуемых чисел $a$ не найдётся.

Ответ:

$n =1$ и $n =2$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#127158Максимум баллов за задание: 7

Дано натуральное число $n.$ Натуральные числа $1,2,...,n$ выписывают на доске в строчку в некотором порядке. У каждых двух стоящих рядом чисел вычисляют их НОД (наибольший общий делитель) и записывают этот НОД на листке. Какое наибольшее количество различных чисел может быть среди всех $n − 1$ выписанных на листке чисел?

Источники: ВСОШ, ЗЭ, 2025, 10.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Давайте начнем с оценки. Вот если есть два различных числа a, b и их НОД равен d, можно ли как-то оценить эти числа, используя d? И как, используя эти оценки, оценить сверху d некоторым выражением от n?

Подсказка 2:

Одна из самых очевидных оценок: min(a, b) ≥ d, max(a, b) ≥ 2d. Отсюда следует, что n ≥ 2d, откуда d ≤ [n / 2]. Осталось привести пример.

Подсказка 3:

Чтобы найти расстановку, для которой любое число d ≤ [n / 2] будет выписано, можно сделать так, чтобы числа вида d и 2d стояли рядом.

Подсказка 4:

Тут на помощь могут прийти числовые цепочки вида a, 2a, 2²a, ... Подумайте, почему они могут быть полезны, и как реализовать расстановку с ними?

Показать ответ и решение

Оценка. Предположим, что какое-то из выписанных на листке чисел больше $⌊n∕2⌋,$ скажем, $НО Д(a,b)= d> ⌊n∕2⌋.$ Тогда наибольшее из чисел $a,b$ не меньше $2d,$ что больше $n$ – противоречие (НОД двух чисел, не превосходящих $n,$ не превосходит $n$ ). Значит, каждый из написанных $Н ОД$ ов не превосходит $⌊n∕2⌋,$ потому количество различных $Н ОД$ ов не может превышать $⌊n∕2⌋.$

Пример. Разобьём все числа от $1$ до $n$ на цепочки вида $k a,2a,4a,8a,...,2a,$ где $a$ — нечётное число, не превосходящее $n.$ Выпишем в строчку цепочки одну за другой. Тогда для любого натурального $d≤ ⌊n∕2⌋$ найдётся цепочка, в которой встречается $d,$ а следующее за $d$ число будет $2d.$ Видим, что каждое натуральное $d≤⌊n∕2⌋$ будет выписано на листке.

Ответ:

$⌊n⌋ 2$

Ошибка.
Попробуйте повторить позже

Задача 3#127159Максимум баллов за задание: 7

Петя и Вася играют в игру на изначально пустой клетчатой таблице $100× 100,$ делая ходы по очереди. Начинает Петя. За свой ход игрок вписывает в некоторую пустую клетку любую заглавную букву русского алфавита (в каждую клетку можно вписать ровно одну букву). Когда все клетки будут заполнены, Петя объявляется победителем, если найдутся четыре подряд идущие клетки по горизонтали, в которых слева направо написано слово «ПЕТЯ», или найдутся четыре подряд идущие клетки по вертикали, в которых сверху вниз написано слово «ПЕТЯ». Сможет ли Петя выиграть независимо от действий Васи?

Источники: ВСОШ, ЗЭ, 2025, 10.1 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте придумать выигрышную стратегию для Васи.

Подсказка 2:

Хорошей идеей будет выбрать некоторую букву, которой нет в слове ПЕТЯ, и некоторым образом с её помощью блокировать появление данного слова. Как это сделать?

Подсказка 3:

Попробуйте придумать такой алгоритм выставления буквы, при котором будет блокироваться появление сочетания букв ПЕ по горизонтали и ТЯ по вертикали. Как нужно отвечать на ходы Пети, чтобы добиться этого?

Показать ответ и решение

Опишем выигрышную стратегию Васи. Пусть Вася все время пишет букву «Ю» в клетку согласно следующим ниже условиям; а если указанная клетка не существует или уже занята, а также если Петя ставит любую букву отличную от «П», «Е», «Т», «Я», то пусть Вася ставит «Ю» в любую свободную клетку.

Если Петя в некоторой клетке пишет букву «П», то Вася пишет «Ю» в клетке, соседней с ней справа; если Петя пишет букву «Е», то Вася пишет «Ю» в клетке, соседней с ней слева; если Петя пишет букву «Т», то Вася пишет «Ю» в клетке, соседней с ней снизу; если Петя пишет букву «Я», то Вася пишет «Ю» в клетке, соседней с ней сверху.

Из первых двух условий следует, что в двух соседних по горизонтали клетках не могло появиться «ПЕ», читаемое слева направо. В самом деле, предположим, что горизонтальное «ПЕ» появилось; тогда после появления первой из этих двух букв Вася, согласно описанной стратегии, сразу займёт место второй из этих букв — противоречие. Аналогично, в двух соседних по вертикали клетках не могло появиться «ТЯ», читаемое сверху вниз.

Ответ:

не сможет

Ошибка.
Попробуйте повторить позже

Задача 4#127160Максимум баллов за задание: 7

Внутри треугольника $ABC$ отмечена точка $P.$ На отрезке $AB$ отмечена точка $Q,$ а на отрезке $AC$ — точка $R$ так, что описанные окружности треугольников $BPQ$ и $CPR$ касаются прямой $AP.$ Через точки $B$ и $C$ провели прямые, проходящие через центр описанной окружности треугольника $BP C,$ а через точки $Q$ и $R$ — прямые, проходящие через центр описанной окружности треугольника $PQR.$ Докажите, что существует окружность, которая касается четырёх проведённых прямых.

Источники: ВСОШ, ЗЭ, 2025, 10.2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Наличие касания двух окружностей с AP должно вызвать у вас желание написать степень точки A относительно этих окружностей.

Подсказка 2:

Скорее всего вы получили равенство AB • AQ = AC • AR, которое говорит о том, что BCQR — вписанный. Попробуйте найти на рисунке какую-нибудь точку, для которой проще всего доказать, что она равноудалена от нужных четырех прямых.

Подсказка 3:

Проще всего это сделать для точки O — центра окружности, описанной около BCRQ. Что для этого нужно доказать?

Подсказка 4:

Пусть O₁, O₂ — центры окружностей (BPC) и (QPR). Для этого достаточно равенства направленных углов O₁BO и OQO₂. Кстати, почему?

Подсказка 5:

Попробуйте выразить угол OQO₂ через углы RPQ и RCQ. Для этого давайте вспомним, что в треугольнике величина центрального угла его описанной окружности, опирающийся на сторону a, некоторым образом связана с величиной угла, противолежащего а. В дальнейшем доказательстве вам поможет теорема об угле между хордой и касательной.

Показать доказательство

Поскольку

2 AB ⋅AQ = AP = AC ⋅AR,

четырёхугольник $BCRQ$ — вписанный. Пусть $O$ — центр окружности $BCRQ.$ Обозначим через $O1$ и $O2$ центры окружностей $BP C$ и $QPR.$ Покажем, что прямые $BO1,$ $CO1,$ $QO2,$ $RO2$ равноудалены от $O.$ Так как

OB = OC =OQ = OR,

для этого достаточно установить равенство направленных углов

∠OCO1 = ∠O1BO =∠OQO2 = ∠O2RO.

Здесь первое и последнее равенства очевидны из симметрии относительно серединных перпендикуляров к $BC$ и $QR.$

Остаётся доказать равенство $∠O1BO = ∠OQO2 (⋆).$ Из счёта углов получаем

∠OQO2 = ∠OQR − ∠O2QR =(90∘ − ∠RCQ )− (90∘− ∠RPQ )=∠RP Q − ∠RCQ

Аналогично

∠O1BO =∠BP C − ∠BQC

Значит, $(⋆)$ эквивалентно равенству

∠RPQ − ∠RCQ =∠BP C − ∠BQC

или

∠BQC − ∠RCQ = ∠BP C− ∠RP Q (⋆⋆).

Из касания окружностей $BPQ$ и $CP R$ следует

∠RPQ = ∠RCP + ∠PBQ,

что из суммы углов четырёхугольника $BP CA$ равно

∠BP C − ∠BAC.

Тем самым, $(⋆⋆)$ преобразуется к виду

∠BQC − ∠RCQ = ∠BAC,

что верно.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 5#127161Максимум баллов за задание: 7

На плоскости отмечены $106$ точек, никакие три из которых не лежат на одной прямой, и проведены все отрезки между ними. Гриша поставил на каждом проведённом отрезке вещественное число, по модулю не превосходящее 1, и для каждой шестёрки отмеченных точек посчитал сумму чисел на всех 15 отрезках, соединяющих их. Оказалось, что каждая такая сумма по модулю не меньше числа $C,$ при этом среди таких сумм есть как положительная, так и отрицательная. При каком наибольшем $C$ это возможно?

Источники: ВСОШ, ЗЭ, 2025, 10.4 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Рассмотрим граф с вершинами в отмеченных точках. Имеются шестёрки с суммами разных знаков. Поскольку мы работаем с кликами, подумайте: какой вид рассуждений о непрерывности может помочь при переходе между шестёрками вершин? Что происходит при замене одной вершины в шестёрке?

Подсказка 2

Если найдутся две шестёрки с разными знаками сумм, отличающиеся одной вершиной, то их объединение содержит 7 вершин. Чем интересно данное множество из 7 вершин? Сколько подшестёрок оно содержит и можно ли сказать что-то про знаки сумм этих шестёрок?

Подсказка 3

Возможно, для анализа данной клики на 7 вершинах стоит её упростить, например, сделав числа на рёбрах одинаковыми.

Подсказка 4

Классифицируйте вершины в этом 7-вершинном множестве: назовите вершину "типа A", если при её удалении сумма в оставшейся шестёрке отрицательна, и "типа B" — если положительна. Пусть k — количество вершин типа A. Какие значения k существенны, а какие аналогичны между собой?

Подсказка 5

Разделите рёбра на три типа: AA (между вершинами типа A), AB (между A и B), BB (между вершинами типа B). Если заменить веса на рёбрах каждого типа на их среднее арифметическое, то как это преобразование повлияет на суммы в подшестёрках? Сохранятся ли условия задачи?

Подсказка 6

Анализировать такую 7-ку вершин намного легче. Можно записать неравенства на искомую константу С при помощи новых значений на ребрах.

Подсказка 7

Какие бы ограничения на константу ни были найдены ранее, всё равно нужно предоставить числа для рёбер, которые будут её реализовывать. Может быть, вид 7-ки после замены чисел на средние можно распространить на весь граф?

Показать ответ и решение

Рассмотрим граф, вершинами которого являются отмеченные точки, а рёбрами — проведённые отрезки.

Оценка. Докажем оценку $15- C ≤ 4 .$ Условие гласит, что в нашем полном графе есть как шестёрки вершин, сумма на рёбрах между которыми положительна, так и шестёрки, сумма на рёбрах между которыми отрицательна. Тогда найдутся две шестёрки, отличающиеся заменой только одной вершины, такие, что у одной из них сумма положительна, у другой отрицательна. В самом деле, возьмём шестёрку с положительной суммой, и будем превращать её в шестёрку с отрицательной суммой, меняя вершины по одной, — на каком-то шаге произошло изменение знака, шестёрки, которые были до и после этого шага – искомая пара.

Далее работаем с полным подграфом на множестве $S$ из семи вершин – объединении вышеописанной пары шестёрок. Рассмотрим все семь шестёрок, которые можно получить выбрасыванием одной вершины из $S.$ Пусть среди них $k$ с отрицательными суммами — получающиеся выбрасыванием вершин $A1,...,Ak,$ будем называть эти вершины $A$ -вершинами, а соответствующие шестёрки – $A$ -шестёрками), и $7− k$ с положительными суммами — получающиеся выбрасыванием вершин $B1,...,B7−k$ (будем называть эти вершины $B$ -вершинами, а соответствующие шестёрки – $B$ -шестёрками). Рёбра между двумя $A$ -вершинами будем называть $AA$ -рёбрами, между двумя $B$ -вершинами — $BB$ -рёбрами, а рёбра, соединяющие $A$ -вершину с $B$ -вершиной — $AB$ -рёбрами.

Из изначальной расстановки чисел на рёбрах, соединяющих вершины множества $S,$ получим новую расстановку, заменив все числа на $AA$ -рёбрах на число $x,$ равное их среднему арифметическому, и аналогично заменив все числа на $AB$ -рёбрах на их среднее арифметическое $y,$ а все числа на $BB$ -рёбрах на их среднее арифметическое $z.$ Очевидно, $|x|≤1,|y|≤ 1,|z|≤ 1,$ так как все старые числа по модулю не превосходят 1.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма. Подграф $S$ с новыми числами на рёбрах удовлетворяет условию с той же константой $C.$

Доказательство леммы. Заметим, что для каждого $AA$ -рёбра есть одно и то же количество $A$ -шестёрок, в которые входят оба его конца. И наоборот, для любой $A$ -шестёрки среди 15 рёбер между её вершинами есть одно и то же количество $AA$ -рёбер. То же верно для $AB$ -рёбер и для $BB$ -рёбер. Значит, сумма $∑A$ чисел на рёбрах в $A$ -шестёрке в новой расстановке есть среднее сумм по всем $A$ -шестёркам в старой расстановке, то есть среднее нескольких чисел, не больших – $C;$ значит, $∑A ≤ −C.$ Аналогичное утверждение верно для сумм в $B$ -шестёрках. Лемма доказана.

_________________________________________________________________________________________________________________________________________________________________________________

Далее изучаем новую расстановку. Рассмотрим случаи.

Случай $k= 1.$ Иными словами, есть ровно одна $A$ -шестёрка, на которой пятнадцать $BB$ -рёбер, и шесть $B$ -шестёрок, на каждой из которых десять $BB$ -рёбер и пять $AB$ -рёбер. Имеем систему неравенств:

15z ≤ −C, 5y +10z ≥ C.

Умножим первое на $−2,$ сложим со вторым, умноженным на 3, получим $15y ≥5C,$ откуда $C ≤ 3.$

Случай $k= 2.$ Теперь у нас две $A$ -вершины и пять $B$ -вершин, то есть на $A$ -шестёрке есть десять $BB$ -рёбер и пять $AB$ -рёбер, а на $B$ -шестёрке – шесть $BB$ -рёбер, восемь $AB$ -рёбер и одно $AA$ -ребро. Имеем

5y+ 10z ≤ −C,

x+ 8y +6z ≥ C

Исключая $z,$ получаем

8C ≤5x+ 25y ≤ 30,

значит, $15 C ≤ 4 .$

Случай $k= 3.$ Аналогично предыдущему, имеем

x+ 8y+ 6z ≤− C

3x+ 9y+ 3z ≥C

Избавляясь на этот раз от $y,$ получаем $17C ≤ 15x − 30z ≤ 45,$ откуда $C ≤ 45< 15. 17 4$

Случаи $k≥ 4$ сводятся к рассмотренным умножением всех чисел на $− 1,$ что ведёт к замене $k ↦→ 7− k.$ Итак, оценка $C ≤ 15 4$ доказана.

Пример. Любое число вершин от двух до 999995 объявим вершинами типа $A,$ остальные – вершинами типа $B.$ На всех рёбрах между двумя вершинами типа $B$ напишем число $− 7, 8$ на всех остальных – число 1. Тогда, если в шестёрке вершин хотя бы пять $B$ -вершин, то сумма в ней не больше $− 15, 4$ а иначе – не меньше $15. 4$

Ответ:

$15 4$

Ошибка.
Попробуйте повторить позже

Задача 6#128205Максимум баллов за задание: 7

На периметре треугольника $ABC$ выбраны точки $D , 1$ $D , 2$ $E , 1$ $E , 2$ $F , 1$ $F 2$ так, что при обходе периметра точки встречаются в порядке $A,$ $F1,$ $F2,$ $B,$ $D1,$ $D2,$ $C,$ $E1,$ $E2.$ Оказалось, что

AD1 = AD2 = BE1 = BE2 = CF1 =CF2.

Докажите, что периметры треугольников, образованных тройками прямых $AD1,$ $BE1,$ $CF1$ и $AD2,$ $BE2,$ $CF2,$ равны.

Источники: ВСОШ, ЗЭ, 2025, 9.8 (см. olympiads.mccme.ru)

Показать доказательство

Начнём со следующей полезной леммы.

Лемма. Пусть точки $F$ и $E$ выбраны соответственно на сторонах $AB$ и $AC$ параллелограмма $ABKC$ так, что $BE =CF.$ Тогда точка $K$ равноудалена от прямых $BE$ и $CF.$

Доказательство. Поскольку $BK ∥EC$ и $CK ∥FB,$ имеем $SKBE =SKBC = SKFC.$ Так как $BE = CF,$ отсюда и следует, что расстояния от точки $K$ до прямых $BE$ и $CF$ равны.

$PIC$

_________________________________________________________________________________________________________________________________________________________________________________

Перейдём к решению. Пусть прямые из условия образуют треугольники $X1Y1Z1$ и $X2Y2Z2$ (точки обозначены как на рис.). Выберем точку $K$ так, что $ABKC$ — параллелограмм; согласно лемме, точка $K$ равноудалена от прямых $BE1,CF1,BE2$ и $CF2$ ; значит, существует окружность с центром $K,$ касающаяся этих прямых в некоторых точках $P1,Q1,P2$ и $Q2$ соответственно. Тогда из равенств отрезков касательных вытекает, что

BX − CX = BP + X P − X Q + CQ =BP +CQ = 1 1 1 1 1 1 1 1 2 2

BP2− X2P2+ X2Q2+ CQ2 = CX2 − BX2.

$PIC$

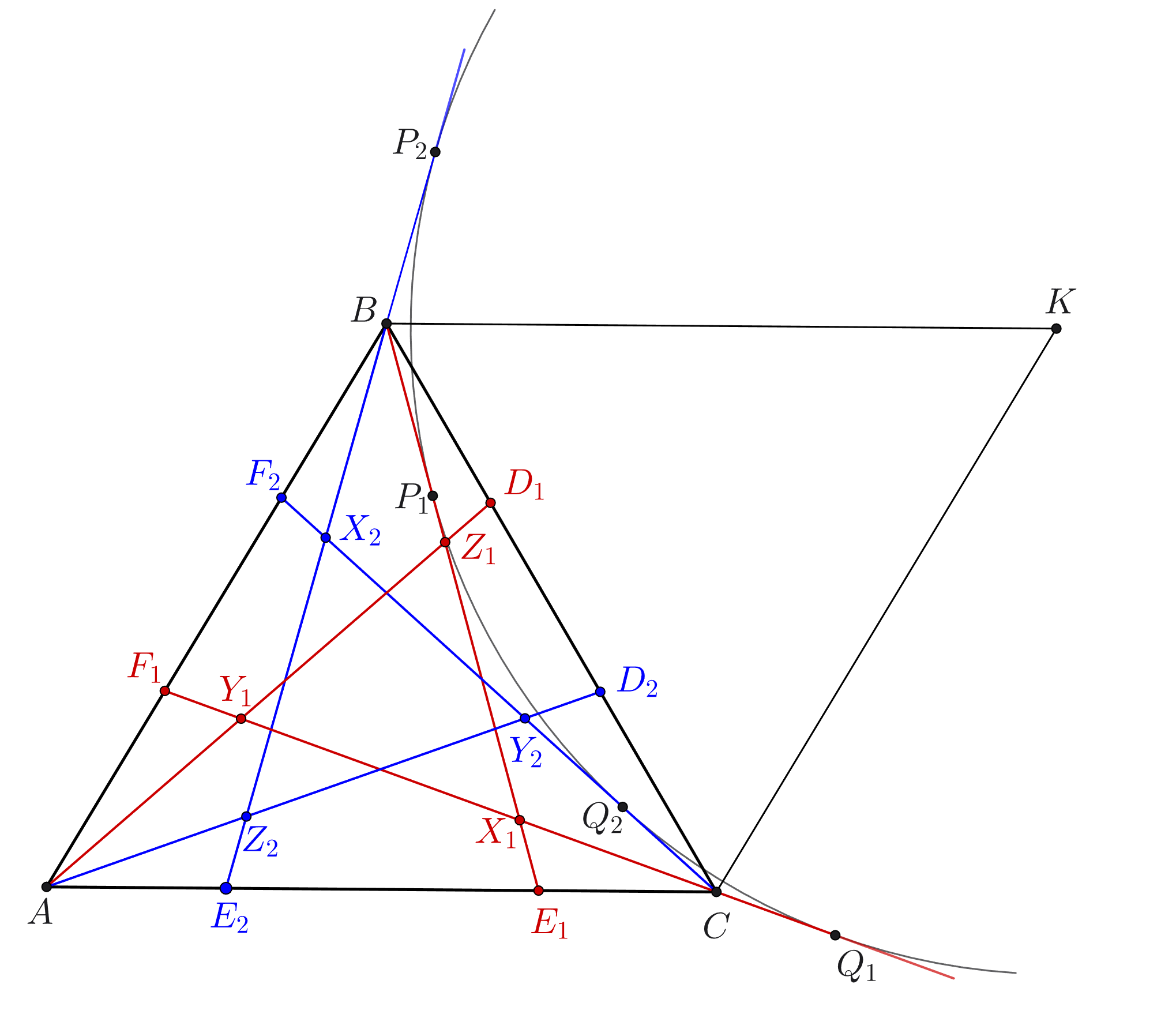
Аналогично получаем, что $CY1− AY1 = AY2− CY2$ и $AZ1− BZ1 =BZ2 − AZ2.$ Складывая полученные три равенства, получаем требуемое равенство периметров.

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#128210Максимум баллов за задание: 7

При каком наименьшем $k$ для любого многочлена $f(x)$ степени 100 с вещественными коэффициентами найдётся такой многочлен $g(x)$ степени не выше $k$ с вещественными коэффициентами, что графики $y = f(x)$ и $y = g(x)$ имеют ровно 100 общих точек?

Источники: ВСОШ, ЗЭ, 2025, 10.6 (см. olympiads.mccme.ru)

Показать ответ и решение

Положим $n= 100.$

Покажем, как подобрать нужный многочлен $g$ степени не выше $n− 2$ для данного многочлена $f$ степени $n.$ При домножении $f$ на ненулевую константу условие не поменяется (многочлен $g$ можно домножить на ту же константу), поэтому считаем, что старший коэффициент $f$ равен $1,$ так что

n n−1 f(x)=x +a1x + ...+an.

Возьмём произвольный набор $n$ различных чисел $x , 1$ $x ,...,x , 2 n$ дающих в сумме $− a , 1$ и положим

h(x)= (x− x1)...(x− xn), g(x)= f(x)− h(x),

так что $h= f − g.$ Видим, что у $f$ и $h$ совпадают коэффициенты при $xn$ и при $xn−1,$ поэтому степень $g$ не превышает $n − 2.$ С другой стороны, абсциссы точек пересечения графиков $f$ и $g$ — это в точности корни многочлена $h,$ а их ровно $n.$

Покажем, что $k ≤n − 3$ не работает. Пусть дан многочлен $f(x)= xn,$ а $g(x)$ — многочлен степени не выше $n− 3.$ Предположим, что графики $f$ и $g$ пересекаются в $n$ точках, имеющих абсциссы $x , 1$ $x,...,x . 2 n$ Но тогда многочлен $f − g$ степени $n$ имеет $n$ вещественных корней $x , 1$ $x,...,x . 2 n$ С другой стороны, у $f − g$ коэффициенты при $xn−1$ и $xn−2$ равны 0. Но тогда по теореме Виета

s1 = x1+ x2+...+xn =0,

s2 = x1x2+ x1x3+...+xn−1xn = 0.

Отсюда

x2+ x2+ ...+x2 =s2− 2s = 0, 1 2 n 1 2

следовательно,

x1 = x2 = ...= xn = 0,

что противоречит тому, что $xi$ различны.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 8#128212Максимум баллов за задание: 7

В программу соревнования входит 25 видов спорта, в каждом из которых определяется один победитель, получающий золотую медаль. В соревновании участвуют 25 спортсменов, каждый — во всех 25 видах спорта. Имеется 25 экспертов, каждый из которых должен сделать прогноз, сколько золотых медалей получит каждый спортсмен, при этом в его прогнозе количества медалей должны являться целыми неотрицательными числами с суммой 25. Эксперта признают компетентным, если он верно угадает количество золотых медалей хотя бы у одного спортсмена. При каком наибольшем $k$ эксперты могут сделать такие прогнозы, что хотя бы $k$ из них будут признаны компетентными независимо от исхода соревнования?

Источники: ВСОШ, ЗЭ, 2025, 10.7 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Казалось бы, задача на оценку + пример. Обычно в этом случае мы сначала делаем оценку, потом под неё подгоняем пример. Здесь же стоит делать наоборот, объясним мотивацию. Пусть мы хотим доказать, что 20 нельзя (например). Доказывать это прямо абсолютно непонятно как, значит, можно попробовать от обратного. Но условие на то, что 20 можно, нам не даёт ровным счётом ничего, мы просто знаем этот факт, и про оценки каждого эксперта мы ничего сказать не можем. В таких случаях оценка чаще всего тривиальна (что-то около границ), а основную сложность составляет пример. Подумайте, какие наборы оценок у экспертов нам лучше использовать для примера?

Подсказка 2:

Поисследуем наборы. Имеем 25 человек и 25 медалей, которые распределены между ними. По принципу Дирихле, всегда найдётся человек, у которого не более одной медали. Что мы тогда можем сказать про спортсменов, у которых вовсе нет медалей (будем называть таких нулевыми)?

Подсказка 3:

Либо среди спортсменов есть хотя бы один нулевой, либо у всех ровно по одной медали. Отлично, то есть нулевых нет только в единственном случае. Значит, можно попробовать организовать высокую вероятность компетенции, основываясь на нулевых. Какой набор (маску) для этого нужно применить?

Подсказка 4:

Разумеется, ту, в которой много нулей, чтобы наверняка хотя бы в один попасть. Однако нельзя забыть про случай, когда у каждого по одной медали. Для этого тоже нужно применить особенную маску, которая будет идентифицировать этот случай. Какую же?

Подсказка 5:

Да, 25 единиц (такую маску назовём единичной). Итого, у одного эксперта единичная маска (назовём его единичным), осталось придумать ещё 24. Причём понятно, что в случае компетентности единичного эксперта мы хотим, чтобы бóльшая часть остальных тоже была компетентна. То есть в остальных масках должно присутствовать много нулей и хотя бы 1 единица. Какая самая тривиальная маска удовлетворяет этим условиям?

Подсказка 6:

Маска вида: 1 единица, 23 нуля и все остальные. Какой набор тогда мы получаем для остальных 24 спортсменов?

Подсказка 7:

Например: (1, 0, ..., 0, 24), (0, 1, 0, ..., 0, 24), ..., (0, ..., 0, 1, 24). Очевидно, если единичный компетентен, то у нас 25 компетентных экспертов. Что же происходит, когда он некомпетентен?

Подсказка 8:

Докажите, что в этом случае хотя бы 3 спортсмена являются нулевыми. Отсюда немедленно следует, что все остальные эксперты компетентны. Итого, имеем пример на 24. Осталось сделать оценку.

Подсказка 9:

Нам нужно доказать, что нет такого набора масок для экспертов, что все всегда компетентны. Это равносильно тому, что всегда можно подобрать такой исход соревнований, что хотя бы один эксперт будет некомпетентным. Придётся разобрать несколько случаев.

Подсказка 10:

Когда у эксперта в маске есть нули и когда их нет. Оба случая достаточно просты. Уверены, вы справитесь. Успехов!

Показать ответ и решение

Оценка. Покажем, что $k≤ 24,$ то есть, что любой эксперт может оказаться некомпетентным. Если этот эксперт считает, что все спортсмены возьмут по одной медали, опровергнем его результатом $(25,0,0,...,0).$ Иначе эксперт считает, что несколько (хотя бы один) спортсменов получат 0 медалей. Тогда распределим все медали между этими спортсменами так, чтобы каждый из них получил хотя бы одну медаль. В таком случае эксперт не угадает ни одного количества медалей.

Пример. Пусть прогноз одного эксперта — $(1,1,1,...,1),$ а прогнозы остальных — (1, 0, …, 0, 24), (0, 1, …, 0, 24), …, (0, 0, …, 1, 24) (на последнем месте 24, и ещё одна единица).

Если некомпетентным оказался первый эксперт, то в исходе точно есть хотя бы три нуля, иначе хотя бы в 23 позициях количество медалей не меньше 2, и тогда общее количество медалей не меньше $23⋅2> 30$ — противоречие. Но тогда каждый из остальных экспертов компетентный.

Предположим теперь, что двое экспертов, отличных от первого, оказались некомпетентными. Тогда в двух позициях их прогнозы — 0 и 1 медалей, а значит, в реальном исходе в этих позициях не менее 2 медалей. Кроме того, ещё в 22 позициях прогнозы обоих экспертов — нули, значит, в реальном исходе в этих позициях не менее 1 медали. Тогда общее количество медалей не меньше $2⋅2+ 22⋅1> 25$ — противоречие.

Ответ: