27.06 Поиск двойных/тройных звездных систем
Ошибка.
Попробуйте повторить позже
Космический инженер решил изучить расположение звёзд для планирования орбитальных станций. Он провёл
кластеризацию звёзд по их позициям на карте. Кластер звёзд — это набор точек, где каждая точка находится от хотя
бы одной другой на расстоянии не более условных единиц. Каждая звезда принадлежит только одному
кластеру.
Двойная система — это два объекта на расстоянии менее , без других звёзд на расстоянии менее
.
Расстояние между точками и
вычисляется как:
Аномалиями называют точки, удалённые более чем на одну условную единицу от кластеров. Их в расчётах не учитываем.
В файле A хранятся данные о звёздах трёх кластеров, где ,
для каждого кластера. В каждой
строке:
,
,
(масса в солнечных массах). Положительная масса (
) — звезда, отрицательная (
)
— нейтронная звезда или чёрная дыра. Количество звёзд не превышает 1200.
В файле B хранятся данные о звёздах четырех кластеров, где ,
для каждого кластера.
Количество звёзд не превышает 5200. Структура данных та же.
Для каждого файла в каждом кластере найдите двойную систему из двух нейтронных звёзд () с
максимальным расстоянием между ними. Вычислите
— среднее арифметическое абсцисс, и
— среднее
арифметическое ординат найденных звёзд.
В ответе запишите целые части четырех чисел через пробел: для A,
для A,
для B,
для B.
Внимание! График приведён для иллюстрации и не связан с заданием. Используйте данные из прилагаемого файла.
Визуализируем данные в , используя «Вставка
Диаграммы
Точечная», чтобы понять структуру
кластеров.
Диаграмма для файла A:
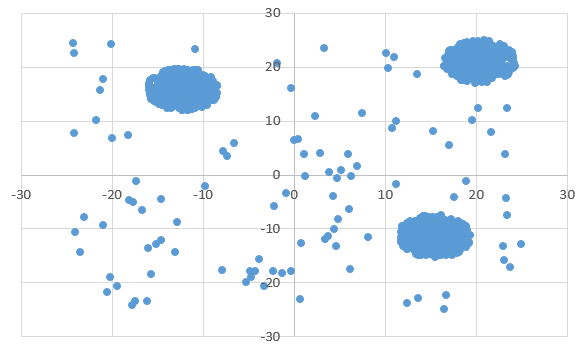
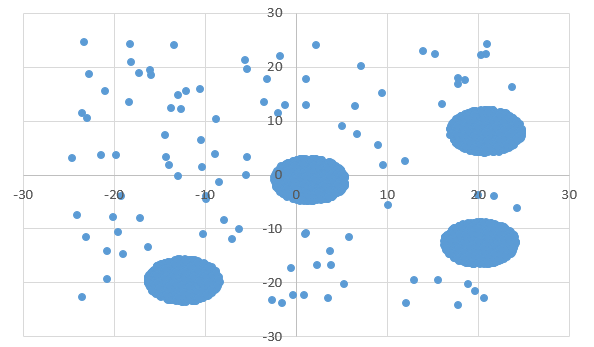
Диаграмма для файла B:
Применяем DBSCAN с радиусом для выделения кластеров, затем с радиусом
для поиска двойных систем.
Фильтруем пары из нейтронных звёзд (
), выбираем ту, где расстояние максимально, и вычисляем
и
.
Код для файла A:
from math import *
def dbscan(a, r):
cl = [] # Инициализируем список для хранения кластеров
while a: # Пока есть элементы в входном массиве ’a’
# Создаем новый кластер и добавляем в него первый элемент из ’a’
cl.append([a.pop(0)])
for i in cl[-1]: # Проходим по элементам последнего кластера
# Проверяем каждый элемент ’j’ в оставшихся элементах ’a’
for j in a[:]:
# Если расстояние между ’i’ и ’j’ меньше радиуса ’r’
x = [i[0], i[1]]
y = [j[0], j[1]]
if dist(x, y) < r:
cl[-1].append(j) # Добавляем ’j’ в текущий кластер
a.remove(j) # Удаляем ’j’ из списка ’a’, чтобы не проверять его снова
return cl
f = open("2_A.txt")
a = [list(map(float, i.replace(",", ".").split())) for i in f]
cl = dbscan(a, 0.8)
cl_total = []
for i in cl:
if len(i) > 10: cl_total.append(i)
t = 0.1
ans = []
for i in cl_total:
found_star = dbscan(i, t)
duo_stars = []
mx_starsys = []
for j in found_star:
if len(j) == 2:
x = [j[0][0],j[0][1]]
y = [j[1][0],j[1][1]]
if -2.7 < j[0][2] < 0 and -2.7 < j[1][2] < 0:
duo_stars.append([x,y])
mx_dist = 0
for j in duo_stars:
if dist(j[0],j[1]) > mx_dist:
mx_mass = dist(j[0],j[1])
mx_starsys = j
ans.append(mx_starsys)
# Рассчитываем среднее значение
res_X = 0
res_Y = 0
for i in ans:
res_X += (i[0][0] + i[1][0])
res_Y += (i[0][1] + i[1][1])
print(int(abs(res_X / 6) * 150))
print(int(abs(res_Y / 6) * 150))
Код для файла B:
from math import *
def dbscan(a, r):
cl = [] # Инициализируем список для хранения кластеров
while a: # Пока есть элементы в входном массиве ’a’
# Создаем новый кластер и добавляем в него первый элемент из ’a’
cl.append([a.pop(0)])
for i in cl[-1]: # Проходим по элементам последнего кластера
# Проверяем каждый элемент ’j’ в оставшихся элементах ’a’
for j in a[:]:
# Если расстояние между ’i’ и ’j’ меньше радиуса ’r’
x = [i[0], i[1]]
y = [j[0], j[1]]
if dist(x, y) < r:
cl[-1].append(j) # Добавляем ’j’ в текущий кластер
a.remove(j) # Удаляем ’j’ из списка ’a’, чтобы не проверять его снова
return cl
f = open("2_B.txt")
a = [list(map(float, i.replace(",", ".").split())) for i in f]
cl = dbscan(a, 0.4)
cl_total = []
for i in cl:
if len(i) > 10: cl_total.append(i)
t = 0.08
ans = []
for i in cl_total:
found_star = dbscan(i, t)
duo_stars = []
mx_starsys = []
for j in found_star:
if len(j) == 2:
x = [j[0][0],j[0][1]]
y = [j[1][0],j[1][1]]
if -2.7 < j[0][2] < 0 and -2.7 < j[1][2] < 0:
duo_stars.append([x,y])
mx_dist = 0
for j in duo_stars:
if dist(j[0],j[1]) > mx_dist:
mx_dist = dist(j[0],j[1])
mx_starsys = j
ans.append(mx_starsys)
# Рассчитываем среднее значение
res_X = 0
res_Y = 0
for i in ans:
res_X += (i[0][0] + i[1][0])
res_Y += (i[0][1] + i[1][1])
print(int(abs(res_X / 8) * 150))
print(int(abs(res_Y / 8) * 150))
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





