Тема Закл (финал) 9 класс

Закл 2017

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 9 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#81696Максимум баллов за задание: 7

Существует ли такая бесконечная возрастающая последовательность $a ,a,a ,... 1 2 3$ натуральных чисел, что сумма любых двух различных членов последовательности взаимно проста с суммой любых трёх различных членов последовательности?

Источники: Всеросс., 2017, ЗЭ, 9.4(см. olympiads.mccme.ru)

Показать ответ и решение

Построим пример такой последовательности. Положим $a = 1,a = 7,a =(3a )!+ 1. 1 2 n+1 n$ Для того, чтобы показать, что она удовлетворяет требованиям, нам придётся эти требования несколько усилить. Будем говорить, что пара (тройка) чисел хорошая, если все её элементы, отличные от единицы, различны (а единица может встретиться в ней несколько раз). Докажем следующее утверждение, из которого будет следовать, что построенная последовательность — требуемая.

Пусть $(ai,aj)$ и $(ap,aq,ar)$ — хорошие пара и тройка элементов последовательности. Тогда НОД $(ai+aj,ap+aq+ ar)=$ НОД $(ai+ aj,ap+ aq− ar)= 1.$

Доказательство проведём индукцией по наибольшему индексу $m$ среди $i,j,p,q$ и $r.$ Если $m = 1,$ утверждение тривиально. Для перехода предположим, что $m >1.$ Число $am$ лежит либо только в паре $(ai,aj),$ либо только в тройке $(ap,aq,ar),$ либо в обеих.

Случай $1.$ Пусть $am$ — только элемент пары; скажем, $am = aj.$ Тогда, поскольку $0 <|ap+aq± ar|≤3am−1,$ число $am − 1 =(3am−1)!$ делится на $|ap +aq± ar|,$ то есть НОД $(ai+ am,ap +aq± ar)=$ НОД $((ai+ 1)+(am − 1),ap+ aq± ar)=$ НОД $(ai+ a1,ap +aq± ar) =1$ по предположению индукции.

Случай $2.$ Пусть $am$ — только элемент тройки; скажем, $am =aq.$ Аналогично, $am − 1$ делится на $ai+ aj,$ так что НОД $(ai+ aj,ap+ am ±ar)=$ НОД $(ai+ aj,ap+ a1±ar)= 1$ по предположению индукции.

Случай $3.$ Пусть $am$ — элемент и пары, и тройки; скажем, $am =aj = aq.$ Тогда $am− 1$ делится на $ap− ai± ar,$ так что НОД $(ai+ am,ap+ am± ar)=$ НОД $(ai+am,(ap+ am ± ar)− (ai+ am))=$ НОД $(ai+ am,ap − ai± ar)=$ НОД $(ai+a1,ap − ai± ar)= 1$ по предположению индукции. Переход индукции доказан.

Ответ:

Да, существует

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#84690Максимум баллов за задание: 7

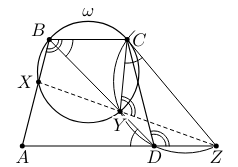
Дана равнобокая трапеция $ABCD$ с основаниями $BC$ и $AD.$ Окружность $ω$ проходит через вершины $B$ и $C$ и вторично пересекает сторону $AB$ и диагональ $BD$ в точках $X$ и $Y$ соответственно. Касательная, проведенная к окружности $ω$ в точке $C,$ пересекает луч $AD$ в точке $Z.$ Докажите, что точки $X,Y$ и $Z$ лежат на одной прямой.

Источники: Всеросс., 2017, ЗЭ, 9.2(см. olympiads.mccme.ru)

Показать доказательство

Поскольку $BC∥AD,$ а прямая $ZC$ касается окружности $ω,$ имеем $∠ADB = ∠YBC = ∠YCZ.$ Следовательно, $∠YDZ + ∠YCZ = 180∘,$ то есть четырёхугольник $CY DZ$ — вписанный.

Значит,

∘ ∠CYZ = ∠CDZ = ∠XBC = 180 − ∠CY X

где последние два равенства следуют из того, что трапеция $ABCD$ равнобокая, а четырёхугольник $XBCY$ вписан в $ω.$ Таким образом, $∠CY Z+ ∠CY X =180∘,$ поэтому точки $X,Y$ и $Z$ лежат на одной прямой.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 3#94744Максимум баллов за задание: 7

В стране некоторые пары городов соединены односторонними прямыми авиарейсами (между любыми двумя городами есть не более одного рейса). Скажем, что город $A$ доступен для города $B,$ если из $B$ можно долететь в $A,$ возможно, с пересадками. Известно, что для любых двух городов $P$ и $Q$ существует город $R,$ для которого и $P,$ и $Q$ доступны. Докажите, что существует город, для которого доступны все города страны. (Считается, что город доступен для себя.)

Источники: Всеросс., 2017, ЗЭ, 9.1(см. olympiads.mccme.ru)

Показать доказательство

Выберем город любой $A$ с наибольшим числом доступных городов. Предположим, что город $B$ не доступен для $A.$ Тогда для некоторого города $C$ доступны оба города $A$ и $B.$ Но тогда для $C$ доступны все города, доступные для $A$ и еще город $B,$ то есть большее количество городов, чем для $A.$ Это противоречит выбору $A,$ значит, для $A$ доступны все города.