Тема Закл (финал) 11 класс

Закл 2016

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 11 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#42964Максимум баллов за задание: 7

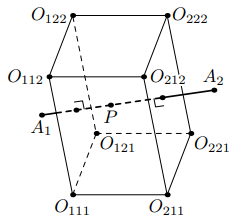
В пространстве даны три отрезка $A A ,B B 1 2 1 2$ и $C C 1 2$ , не лежащие в одной плоскости и пересекающиеся в одной точке $P$ . Обозначим через $Oijk$ центр сферы, проходящей через точки $Ai,Bj,Ck$ и $P$ . Докажите, что прямые $O111O222,O112O221,O121O212$ и $O211O122$ пересекаются в одной точке.

Источники: Всеросс., 2016, ЗЭ, 11.2(см. vos.olimpiada.ru)

Подсказки к задаче

Подсказка 1!

Если попробовать в голове представить такое пространственное сложное чудо, можно заметить, что O_(ijk) образуют что-то очень похожее на параллелепипед. Попробуйте доказать, что они образуют параллелепипед (а его диагонали, как мы знаем, пересекаются в одной точке). Еще к такой мысли можно прийти так - вас просят в пространстве доказать, что какие-то прямые пересекутся в одной точке. Мы знаем что-то про пересечение в пространстве у не очень большого числа объектов пока.

Подсказка 2!

Итак, хотим доказать что это параллелепипед. Построим серединный перпендикуляр к отрезкам A₁P, A₂P. Тогда O_(1jk) принадлежит этому перпендикуляру, так как A₁ и P лежат на каждой сфере такой. И A₂, P - так же. теперь попробуем заметить, что эти два серединных перпендикуляра (к A₁P и A₂P) будут параллельны(почему?).

Подсказка 3!

Так-так -так, вот мы и нашли какие-то параллельные плоскости. Давайте теперь попробуем найти еще несколько пар параллельных плоскостей, и докажем, что вышел именно нужный нам параллелепипед.

Показать доказательство

Для любого отрезка $XY$ серединным перпендикуляром к этому отрезку назовем плоскость, перпендикулярную ему и проходящую через его середину, т. е. геометрическое место точек, равноудаленных от $X$ и $Y.$

Пусть $αi,i∈{1,2}$ — серединный перпендикуляр к отрезку $PAi.$ Тогда $Oijk ∈αi$ (поскольку на каждой такой сфере лежат обе точки $Ai,P).$ Легко видеть, что $α1 ∥α2,$ поскольку обе перпендикулярны прямой $A2A1.$ Аналогично определим плоскости $βj :β1 ∥ β2$ для $B1,B2,P$ и $γk$ для $C1,C2,P.$ Поскольку шесть выбранных плоскостей попарно параллельны, то они образуют параллелепипед, осталось заметить, что его вершинами будут точки $Oijk.$ Действительно, каждая точка лежит в $3$ плоскостях $O121 ∈ α1,β2,γ1$ (например), откуда и следует нужное. Учитывая, что диагонали параллелепипеда пересекаются в одной точке, всё доказано.

$PIC$