Регион 2024

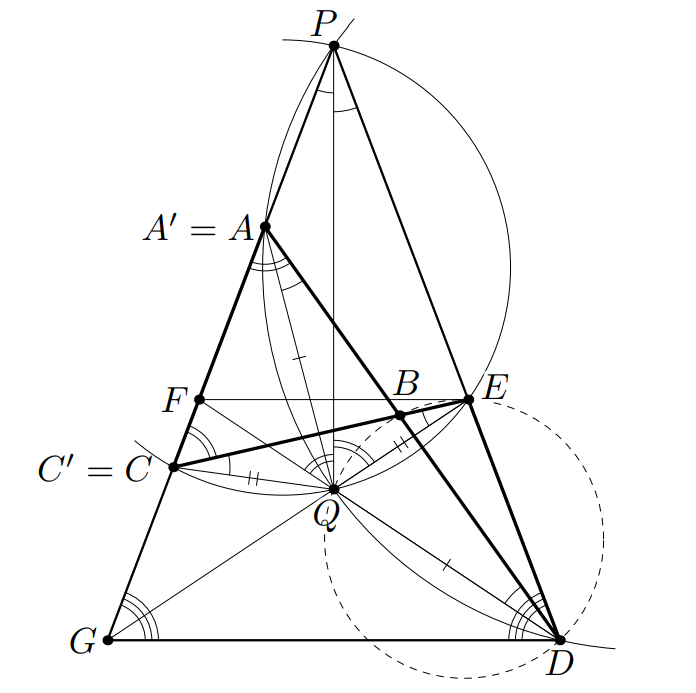
Первое решение. Обозначим через середину дуги окружности, описанной около треугольника Прямая является внешней биссектрисой в треугольнике а следовательно, и в треугольнике Но треугольник равнобедренный, поэтому

Заметим далее, что Таким образом, в равнобедренных треугольниках и равны углы при вершинах, а также основания, поэтому равны и сами треугольники. Отсюда, во-первых,

Во-вторых, расстояние от точки до прямой равно расстоянию от точки до а последнее равно расстоянию от до (поскольку ). Значит, точка лежит на биссектрисе угла между прямыми и

Из условия вытекает, что эта биссектриса является серединным перпендикуляром к отрезку Таким образом, Иными словами, точка — центр окружности, описанной около треугольника Следовательно,

что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Для начала сделаем замечание. Пусть на прямой выбраны точки и такие, что и тогда и Действительно, если это не так и, скажем, точки и лежит на луче то

что невозможно.

Построим теперь такие точки. Пусть прямые и пересекаются в точке для определённости, пусть лежит на луче Выберем на прямой точку такую, что Тогда — трапеция с равными углами при основании; следовательно, и Пусть диагонали и пересекаются в точке Пусть, наконец, описанные окружности треугольников и вторично пересекают прямую в точках и соответственно.

Поскольку — биссектриса угла получаем и Кроме того,

Значит, поэтому треугольник получается из поворотом вокруг точки Отсюда нетрудно получить, что Далее, из вписанности и симметрии имеем

По замечанию выше получаем, что и

Осталось завершить решение. Имеем Отсюда следует, что точки и лежат на одной окружности. Значит,

что и требовалось доказать.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. Если то точка совпадает с что невозможно. Поэтому можно считать, что прямые и пересекаются. Кроме того, можно показать, что в условиях задачи всегда лежит именно на луче

______________________________________________________________________________________________________________________________________________________

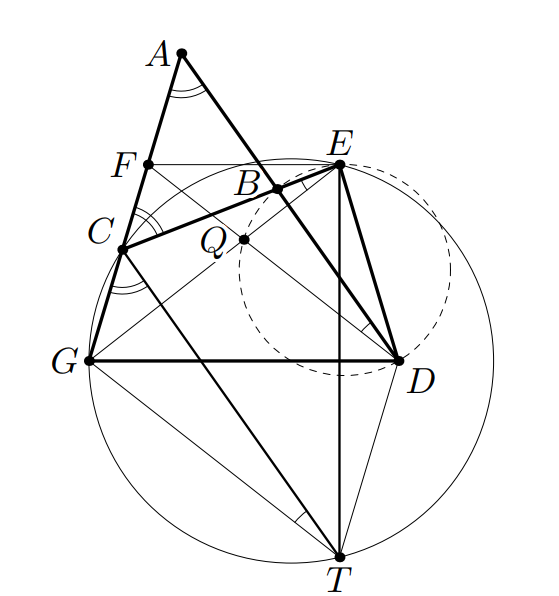
Третье решение. Как и в предыдущем решении, достроим равнобокую трапецию с точкой пересечения диагоналей Как мы видели в том же решении, достаточно доказать, что точки и лежат на одной окружности.

Выберем точку так, что четырёхугольник — параллелограмм. Тогда — также параллелограмм, ибо Значит, и

первое равенство означает, что лежит на серединном перпендикуляре к а второе — что это внешняя биссектриса угла Но, как известно, эта внешняя биссектриса вторично пересекает описанную окружность треугольника в точке, лежащей на серединном перпендикуляре к значит, и есть эта точка, и точки лежат на одной окружности.

Наконец, из этой окружности и двух параллелограммов получаем

то есть точки и лежат на одной окружности; это мы и хотели доказать.