Тема Регион 11 класс

Регион 2016

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела регион 11 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#102213Максимум баллов за задание: 7

В пространстве расположены $2016$ сфер, никакие две из них не совпадают. Некоторые из сфер — красного цвета, а остальные зеленого. Каждую точку касания красной и зеленой сферы покрасили в синий цвет. Найдите наибольшее возможное количество синих точек.

Источники: Всеросс., 2016, РЭ, 11.6(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Оценка в этой задаче делается совсем не сложным образом. Вам нужно лишь вспомнить, что две сферы могут касаться только в 1 точке. Что же делать с примером? Нужно как-то удачно расположить сферы между собой. Подумайте, как это можно сделать.

Подсказка 2

Для начала убедимся, что оценка на 1008² у нас с вами совпала. Как можно в теории получить это число? Нужно, чтобы одна сфера зелёного цвета, например, касалась остальных 1008 красных(отсюда понятно, что радиусы у них можно взять одинаковый). Тогда, учитывая все 1008 зелёных сфер, получим требуемое. Теперь подумайте в этом направлении.

Подсказка 3

Самый простой способ располагать красные сферы - это разместить их на какой-нибудь удобной окружности. Осталось только понять, как расположить зелёные сферы(и немного, технически описать радиусы всех сфер), и победа!

Показать ответ и решение

Пусть среди сфер есть $r$ красных и $2016− r$ зелёных. Так как у любых двух сфер максимум одна точка касания, количество синих точек не превосходит $2 2 2 r(2016− r) =1008 − (1008− r) ≤1008.$

Предъявим пример с таким количеством синих точек. Пусть $ℓ$ — некоторая прямая, $α$ — плоскость, перпендикулярная $ℓ$ и пересекающая её в точке $O,$ а $ω$ — окружность с центром $O$ и радиусом $1,$ лежащая в $α.$ Построим $1008$ красных сфер одинакового радиуса $r< 1$ с различными центрами $R1,R2,...,R1008,$ лежащими на $ω.$

$PIC$

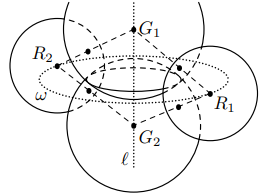
Пусть $G1,G2,...,G1008$ — различные точки на $ℓ,$ удалённые от $O$ на расстояния $d1,d2,...,d1008.$ Тогда расстояние между $Gi$ и любой точкой $Rj$ равно $∘ ----- 1+ d2i.$ Значит, если мы построим зелёную сферу с центром $Gi$ и радиусом $∘ ----- 1+ d2i − r,$ она будет касаться всех красных сфер. При этом все точки касания будут попарно различными, поскольку они лежат на отрезках вида $RjGi,$ которые не имеют общих точек, кроме концов. Значит, в нашей конструкции действительно будут отмечены $10082$ синих точек.

Замечание. Все красные сферы в этом примере получаются друг из друга вращением вокруг прямой $ℓ.$ Поэтому, если зелёная сфера, центр которой лежит на $ℓ,$ касается одной красной сферы, то она касается и всех красных сфер.

Ответ:

$10082 =1016064$ точек