Тема Кинематика

00 Задания Школково

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела кинематика

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#73673Максимум баллов за задание: 2

На равномерно вращающемся диске жук переместился из точки $B$ в точку $A$ (см. рисунок). Как при этом изменились линейная скорость жука и частота его обращения вокруг оси $O$ ?

$PIC$

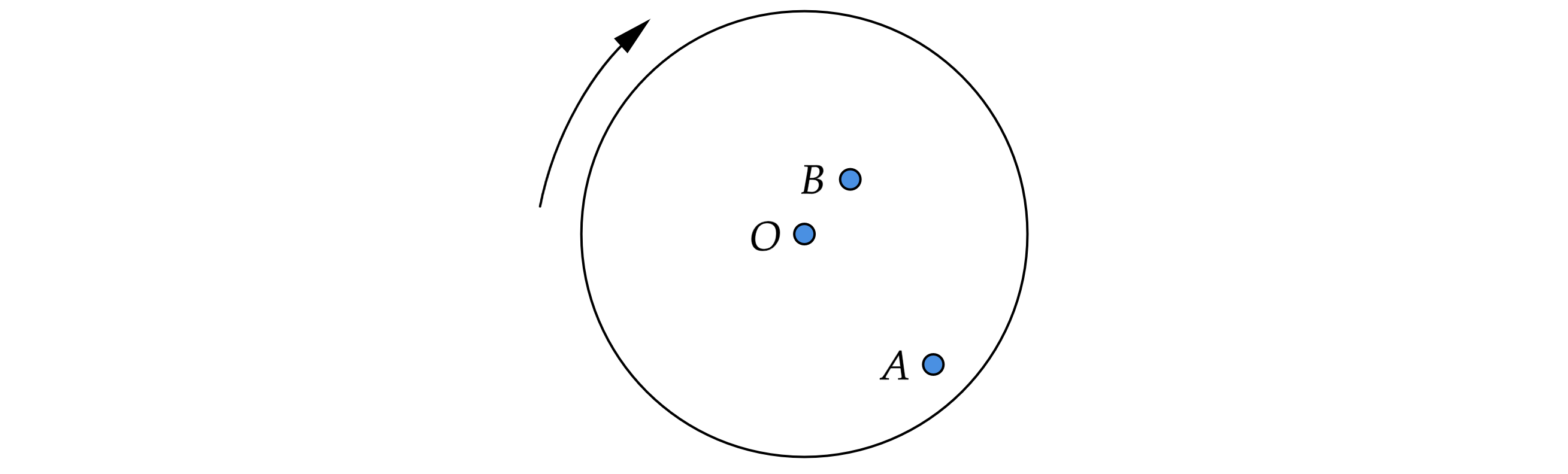
Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

|-----------------|-----------------| |Линейная скорость |Частота обращ ения | |------жука-------|------ж-ука-------| | | | -------------------------------------

Показать ответ и решение

А) При перемещении из точки $B$ в точку $A$ увеличивается радиус обращения жука относительно точки $O$ . Поскольку период обращения диска не изменяется, то не изменяется и угловая скорость вращения диска. Формула для нахождения линейной скорости $v = ω⋅R$ , где $ω$ - угловая скорость обращения. Поскольку радиус $R$ станет больше, то и линейная скорость станет больше. Ответ – 1

Б) Частота с периодом связана следующей формулой $ν = 1- T$ , поскольку период обращения не изменился, то и частота обращения не изменилась. Ответ – 3

Ответ: 13

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#73671Максимум баллов за задание: 2

Космический корабль, движущийся по круговой орбите вокруг Земли, сместился на другую круговую орбиту, меньшего радиуса. Как изменились в результате этого перехода модуль скорости корабля и период его обращения вокруг Земли? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

|----------------|------------------------| |Скорость корабля|Период обращения-корабля-| ------------------------------------------|

Показать ответ и решение

$PIC$

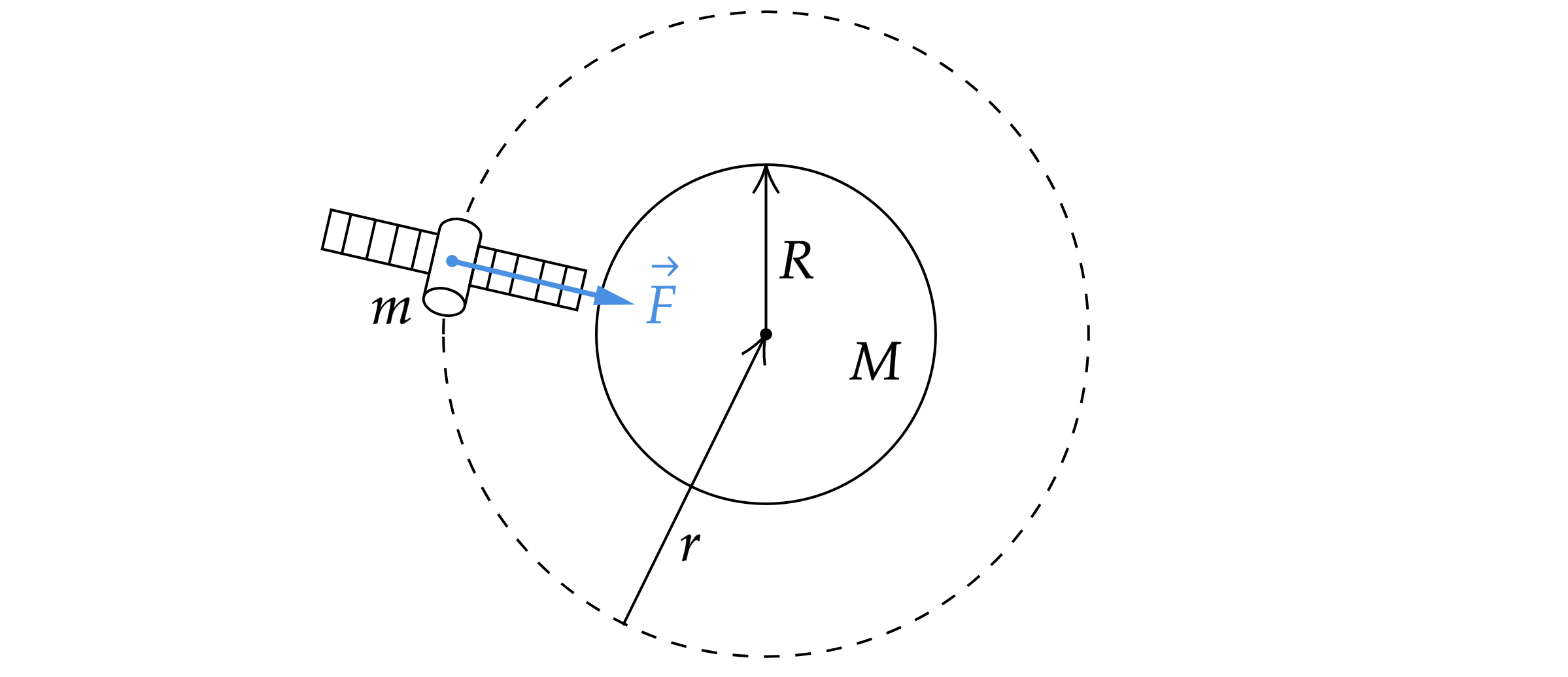
По закону всемирного тяготения, сила тяготения, действующая на корабль со стороны Земли, равна

mM F = G -r2-- (1)

где $m$ – масса корабля, $M$ – масса Земли, $r$ – радиус орбиты корабля, движущегося вокруг Земли, $R$ - радиус Земли.
Тогда при уменьшении радиуса орбиты $r$ сила тяготения $F$ , действующая на корабль со стороны Земли, будет увеличиваться. По второму закону Ньютона сила тяготения будет равна