Графики функций
Готовиться с нами - ЛЕГКО!

График какой из приведенных ниже функций изображен на рисунке?
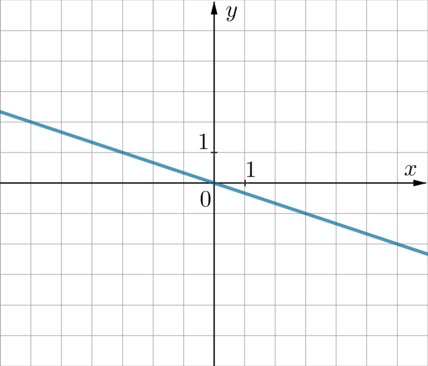
1) \(y=-\dfrac13x\qquad\) 2) \(y=-3x\qquad \) 3) \(y=\dfrac13x\qquad \) 4) \(y=3x\)
Способ 1.
Так как прямая проходит через 2 и 4 четверти (“наклонена влево” относительно вертикального положения), то имеет вид \(y=kx\), где \(k\) – отрицательное число. Следовательно, выбор стоит между 1 и 2 пунктами. Так как прямая наклонена ближе к оси \(Ox\), чем к оси \(Oy\), то \(|k|<1\). Следовательно, ответ 1.
Способ 2.
Исходя из того, что прямая проходит через начало координат \((0;0)\), ее уравнение имеет вид \(y=kx\). Заметим, что прямая проходит через точку \(x=3, y=-1\). Подставим: \(-1=k\cdot 3\), откуда \(k=-\frac13\). Следовательно, уравнение имеет вид \(y=-\frac13x\) и правильный ответ 1.
График какой из приведенных ниже функций изображен на рисунке?
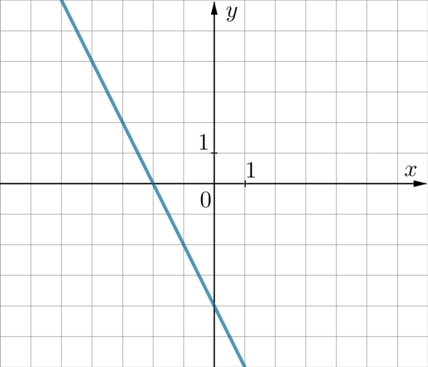
1) \(y=2x-4\qquad\) 2) \(y=-2x+4\qquad \) 3) \(y=2x+4\qquad \) 4) \(y=-2x-4\)
Способ 1.
Так как прямая проходит через 2 и 4 четверти (“наклонена влево” относительно вертикального положения), то имеет вид \(y=kx+b\), где \(k\) – отрицательное число. Следовательно, выбор стоит между 2 и 4 пунктами. Во 2-ом пункте записано уравнение прямой, которая поднята на 4 единицы вверх относительно прямой \(y=-2x\) (проходящей через начало координат). Прямая на рисунке наоборот опущена на 4 единицы вниз. Следовательно, выбираем пункт 4.
Способ 2.
Прямая имеет вид \(y=kx+b\). Из рисунка видно, что она проходит через точку с координатами \(x_1=-2, y_1=0\) и точку \(x_2=0, y_2=-4\). Подставим: \[\begin{cases} 0=-2k+b\\ -4=0+b \end{cases} \quad\Rightarrow\quad \begin{cases} k=-2 \\ b=-4\end{cases}\] Значит, уравнение имеет вид \(y=-2x-4\) и правильный ответ 4.
График какой из приведенных ниже функций изображен на рисунке?
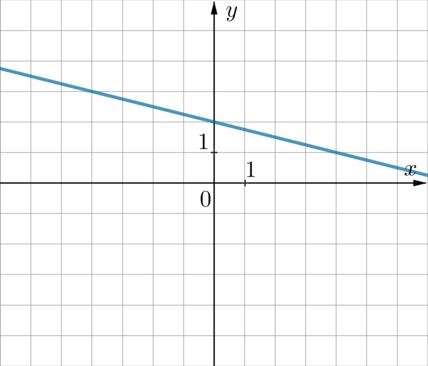
1) \(y=\dfrac14x+2\qquad\) 2) \(y=\dfrac14x-2\qquad \) 3) \(y=-\dfrac14x+2\qquad \) 4) \(y=-\dfrac14x-2\)
Способ 1.
Так как прямая “наклонена влево” относительно вертикального положения (проходит через 2 и 4 четверти, если продлить ее вправо), то имеет вид \(y=kx+b\), где \(k\) – отрицательное число. Следовательно, выбор стоит между 3 и 4 пунктами. В 3-ем пункте записано уравнение прямой, которая поднята на 2 единицы вверх относительно прямой \(y=-\frac14x\) (проходящей через начало координат). Так же, как на данном рисунке. Следовательно, выбираем пункт 3.
Способ 2.
Прямая имеет вид \(y=kx+b\). Из рисунка видно, что она проходит через точку с координатами \(x_1=4, y_1=1\) и точку \(x_2=0, y_2=2\). Подставим: \[\begin{cases} 1=4k+b\\ 2=0+b \end{cases} \quad\Rightarrow\quad \begin{cases} k=-\frac14 \\[1ex] b=2\end{cases}\] Значит, уравнение имеет вид \(y=-\frac14x+2\) и правильный ответ 3.
График какой из приведенных ниже функций изображен на рисунке?
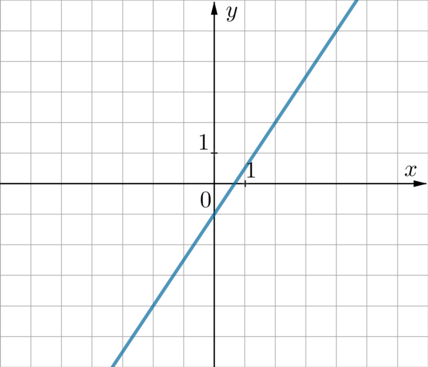
1) \(y=-\dfrac32x+1\qquad\) 2) \(y=-\dfrac32x-1\qquad \) 3) \(y=\dfrac32x-1\qquad \) 4) \(y=\dfrac32x+1\)
Способ 1.
Так как прямая “наклонена вправо” относительно вертикального положения (проходит через 1 и 3 четверти), то имеет вид \(y=kx+b\), где \(k\) – положительное число. Следовательно, выбор стоит между 3 и 4 пунктами. В 3-ем пункте записано уравнение прямой, которая опущена на 1 единицу вниз относительно прямой \(y=\frac32x\) (проходящей через начало координат). Так же, как на данном рисунке. Следовательно, выбираем пункт 3.
Способ 2.
Прямая имеет вид \(y=kx+b\). Из рисунка видно, что она проходит через точку с координатами \(x_1=0, y_1=-1\) и точку \(x_2=2, y_2=2\). Подставим: \[\begin{cases} -1=0+b\\ 2=2k+b \end{cases} \quad\Rightarrow\quad \begin{cases} k=\frac32 \\[1ex] b=-1\end{cases}\] Значит, уравнение имеет вид \(y=\frac32x-1\) и правильный ответ 3.
График какой из приведенных ниже функций изображен на рисунке?

1) \(y=-\dfrac32x+1\qquad\) 2) \(y=-\dfrac32x-1\qquad \) 3) \(y=\dfrac32x-1\qquad \) 4) \(y=\dfrac32x+1\)
Способ 1.
Так как прямая “наклонена вправо” относительно вертикального положения (проходит через 1 и 3 четверти), то имеет вид \(y=kx+b\), где \(k\) – положительное число. Следовательно, выбор стоит между 3 и 4 пунктами. В 3-ем пункте записано уравнение прямой, которая опущена на 1 единицу вниз относительно прямой \(y=\frac32x\) (проходящей через начало координат). Так же, как на данном рисунке. Следовательно, выбираем пункт 3.
Способ 2.
Прямая имеет вид \(y=kx+b\). Из рисунка видно, что она проходит через точку с координатами \(x_1=0, y_1=-1\) и точку \(x_2=2, y_2=2\). Подставим: \[\begin{cases} -1=0+b\\ 2=2k+b \end{cases} \quad\Rightarrow\quad \begin{cases} k=\frac32 \\[1ex] b=-1\end{cases}\] Значит, уравнение имеет вид \(y=\frac32x-1\) и правильный ответ 3.
На одном из рисунков изображен график функции \(y=5x\). Укажите номер этого рисунка.
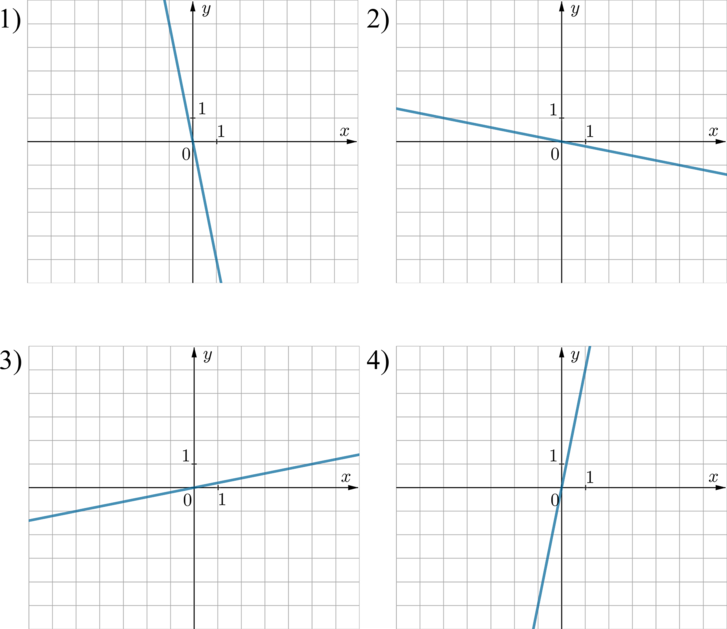
Способ 1.
Так как уравнение прямой имеет вид \(y=5x\), то есть свободный член равен нулю, то прямая проходит через начало координат. Так как коэффициент перед \(x\) положительный, то она проходит через 1 и 3 четверти (“наклонена вправо” относительно вертикального положения). Следовательно, выбираем между 3 и 4 пунктами. Так как коэффициент перед \(x\) по модулю больше 1, то прямая должна быть наклонена ближе к оси \(Oy\). Поэтому выбираем ответ 4.
Способ 2.
Из формулы \(y=5x\) следует, что прямая проходит, например, через точку с координатами \(x=1, y=5\). Из рисунков видно, что единственная прямая, которая проходит через эту точку, это прямая в пункте 4.
На одном из рисунков изображен график функции \(y=x-5\). Укажите номер этого рисунка.
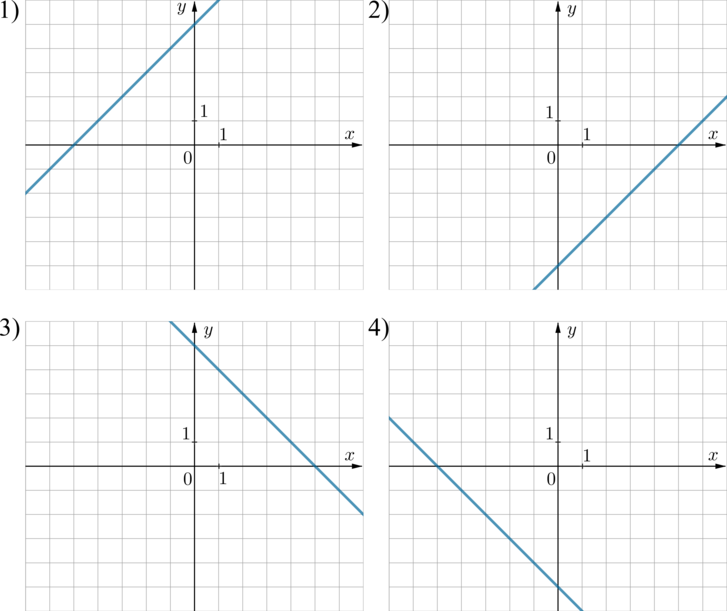
Способ 1.
Так как уравнение прямой имеет вид \(y=x-5\), то есть коэффициент перед \(x\) положительный, то она “наклонена вправо” относительно вертикального положения. Поэтому выбираем между пунктами 1 и 2. Так как свободный коэффициент равен \(-5\), то прямая опущена на 5 единиц вниз по оси \(Oy\) относительно прямой \(y=x\) (которая проходит через начало координат). Поэтому ответ 2.
Способ 2.
Из формулы \(y=x-5\) следует, что прямая проходит, например, через точку с координатами \(x=5, y=0\). Из рисунков видно, что через эту точку проходят прямые из пунктов 2 и 3. Заметим, что прямая \(y=x-5\) также проходит через точку \(x=0, y=-5\). Среди прямых под номерами 2 и 3 через эту точку проходит только прямая 2.



