Неравенства и их системы
Готовиться с нами - ЛЕГКО!

Какие из следующих чисел являются решениями неравенства \(5x-6\leqslant 18-7x\)?
1) \(5\)
2) \(-1\)
3) \(2\)
4) \(7\)
В ответе укажите номера выбранных ответов в порядке возрастания без запятых, пробелов и других дополнительных символов.
Решим неравенство: \[5x-6\leqslant 18-7x\quad\Leftrightarrow\quad 5x+7x\leqslant 18+6\quad\Leftrightarrow \quad 12x\leqslant 24\quad\Leftrightarrow\quad x\leqslant 2\] Следовательно, подходят ответы 2 и 3.
Можно было не решать неравенство и проверить, является ли число решением неравенства так: подставить число в неравенство и проверить, верное/неверное неравенство мы получаем. Например, подставим \(5\) и получим \(25-6\leqslant 18-35\), откуда \(19\leqslant -17\). Это неравенство неверное, следовательно, \(5\) не является решением.
Укажите множество решений неравенства \(5x\geqslant x+12\).
1) \((-\infty;2]\)
2) \([2;+\infty)\)
3) \((-\infty;3]\)
4) \([3; +\infty)\)
Решим неравенство: \[5x-x\geqslant 12\quad\Leftrightarrow\quad 4x\geqslant 12\quad\Leftrightarrow\quad x\geqslant 3\] Следовательно, ответ \(x\in [3; +\infty)\).
Укажите множество решений неравенства \(x-1\geqslant 3x+2\).

Решим неравенство \[x-3x\geqslant 2+1\quad\Leftrightarrow\quad -2x\geqslant 3\quad\Leftrightarrow\quad x\leqslant -\dfrac32\] Следовательно, решения неравенства \(x\in (-\infty; -1,5]\). Значит, ответ 1.
Укажите множество решений неравенства \(-6-x\geqslant 2x-9\).
1) \(x\leqslant 1\)
2) \(x\geqslant 1\)
3) \(x\leqslant 5\)
4) \(x\geqslant 5\)
Решим неравенство \[-6+9\geqslant 2x+x\quad\Leftrightarrow\quad 3\geqslant 3x\quad\Leftrightarrow\quad x\leqslant 1\] Значит, ответ 1.
Укажите множество решений неравенства \(3-x<3x+5\).
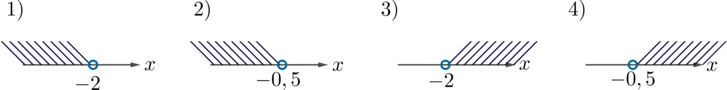
Решим неравенство \[3-5<3x+x\quad\Leftrightarrow\quad 4x>-2\quad\Leftrightarrow\quad x>-\dfrac12\] Следовательно, решения \(x\in (-0,5; +\infty)\), значит, ответ 4.
При каких \(x\) значение выражения \(5x-3\) больше значения выражения \(3x+5\)?
1) \(x>1\)
2) \(x<1\)
3) \(x>4\)
4) \(x<4\)
Из условия получаем неравенство \[5x-3>3x+5\quad\Leftrightarrow\quad 5x-3x>5+3\quad \Leftrightarrow\quad 2x>8\quad\Leftrightarrow\quad x>4\]Значит, ответ 3.
Укажите множество решений неравенства \(2(x-5)\leqslant -6\).
1) \([2; +\infty)\)
2) \((-\infty;2]\)
3) \((-\infty;-8]\)
4) \([-8; +\infty)\)
Решим неравенство \[2x-10\leqslant -6\quad\Leftrightarrow\quad 2x\leqslant -6+10\quad\Leftrightarrow\quad x\leqslant 2\] Ответ 2.



