Радиус, длина и центр окружности (страница 3)
Готовиться с нами - ЛЕГКО!

В окружности с центром \(O\) \(AC\) и \(BD\) – диаметры. Центральный угол \(AOD\) равен \(110^\circ\). Найдите вписанный угол \(ACB\). Ответ дайте в градусах.
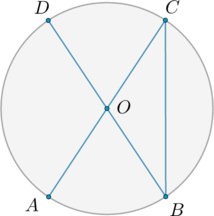
Так как \(BD\) – диаметр, то \(\angle BOD=180^\circ\), следовательно, \(\angle AOB=180^\circ-\angle AOD=70^\circ\). \(\angle AOB\) и \(\angle ACB\) – центральный и вписанный углы соответственно, опирающиеся на одну и ту же дугу, следовательно, \(\angle ACB=\angle AOB:2=35^\circ\).
\(AC\) и \(BD\) – диаметры окружности с центром \(O\). Угол \(ACB\) равен \(38^\circ\). Найдите угол \(AOD\). Ответ дайте в градусах.

Так как \(\angle ACB\) – вписанный угол, то центральный угол \(AOB\), который опирается на ту же дугу, что и \(ACB\), в два раза больше: \(\angle AOB=2\cdot 38^\circ=76^\circ\). Так как \(BD\) – диаметр, то угол \(BOD\) – развернутый и равен \(180^\circ\), следовательно, \(\angle AOD=180^\circ-\angle AOB=104^\circ\).
Точки \(A, B, C\), расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как \(1:3:5\). Найдите больший угол треугольника \(ABC\). Ответ дайте в градусах.
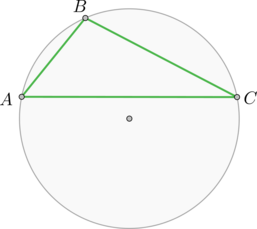
Пусть дуги \(AB=x\), \(BC=3x\), \(AC=5x\). Так как градусная мера всей окружности равна \(360^\circ\), то \(x+3x+5x=360^\circ\), откуда \(x=40^\circ\).
Из вписанных углов \(\angle ABC\), \(\angle ACB\) и \(\angle BAC\) большим будет тот, который опирается на большую дугу, то есть на дугу \(AC\), равную \(5\cdot 40^\circ=200^\circ\). Так как вписанный угол равен половине дуги, на которую он опирается, то \(\angle ABC=100^\circ\).
Хорда \(AB\) делит окружность на две дуги, градусные меры которых относятся как \(5:7\). Под каким углом видна эта хорда из точки \(C\), принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
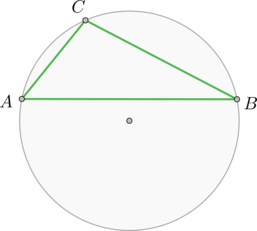
Так как градусные меры дуг относятся как \(5:7\), то можно ввести обозначения: \(5x\) – градусная мера меньшей дуги, \(7x\) – большей. Тогда \(5x+7x=360^\circ\), откуда \(x=30^\circ\).
Нужно найти \(\angle ACB\). Он является вписанным и равен половине большей дуги, следовательно, равен \(0,5\cdot 7x\), или \(105^\circ\).
Дуга окружности \(AC\), не содержащая точки \(B\), имеет градусную меру \(200^\circ\), а дуга окружности \(BC\), не содержащая точки \(A\), имеет градусную меру \(80^\circ\). Найдите вписанный угол \(ACB\). Ответ дайте в градусах.
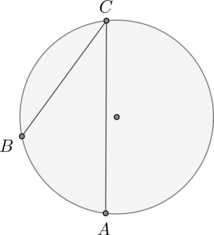
Так как градусная мера всей окружности равна \(360^\circ\), то дуга \(AB\), не содержащая точки \(C\), равна \(360^\circ-200^\circ-80^\circ=80^\circ\). Так как вписанный угол равен половине дуги, на которую он опирается, то \(\angle ACB\) равен \(40^\circ\).
Найдите вписанный угол, опирающийся на дугу, длина которой равна \(\frac15\) длины окружности. Ответ дайте в градусах.
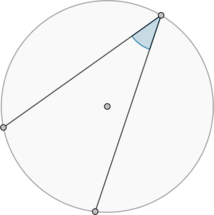
Рассмотрим рисунок:
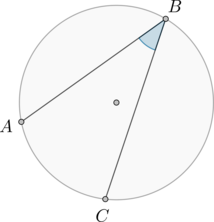
Так как длина меньшей дуги \(AC\) равна \(\frac15\) длины окружности, то и ее градусная мера равна \(\frac15\) градусной меры окружности, то есть равна \(\frac15\cdot 360^\circ=72^\circ\). Угол \(ABC\) – вписанный, опирающийся на меньшую дугу \(AC\), следовательно, равен ее половине, то есть \(36^\circ\).
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Обозначим хорду за \(AB\). Рассмотрим \(\triangle AOB\), где \(O\) – центр окружности.
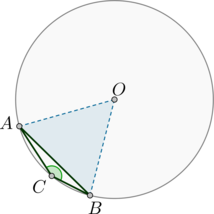
Так как \(AB\) равна радиусу окружности, то \(\triangle AOB\) – равносторонний. Следовательно, \(\angle AOB=60^\circ\).
Следовательно, меньшая дуга \(AB\) окружности равна \(\angle
AOB=60^\circ\). Тогда большая дуга \(AB\) окружности равна \(360^\circ-60^\circ=300^\circ\). Заметим, что \(\angle ACB\) – вписанный угол, опирающийся на большую дугу \(AB\), следовательно, он равен ее половине, то есть \(\angle ACB=150^\circ\).



