Площадь трапеции (страница 2)
Готовиться с нами - ЛЕГКО!

Основания равнобедренной трапеции равны \(7\) и \(13\), а ее площадь равна \(40\). Найдите периметр трапеции.

Проведем высоту \(BH\).

Площадь трапеции равна \[40=\dfrac{AD+BC}2\cdot BH=\dfrac{7+13}2\cdot BH\quad\Rightarrow\quad BH=
4\] Рассмотрим прямоугольный \(\triangle ABH\). По свойству равнобедренной трапеции \(AH=(AD-BC):2=(13-7):2=3\). Следовательно, \[AB=\sqrt{AH^2+BH^2}=5\] Тогда периметр трапеции равен \(5+5+7+13=30\).
В трапеции \(ABCD\) с основаниями \(BC = 5\) и \(AD = 2\cdot BC\) проведена высота \(BE\). Найдите отношение площади трапеции к длине этой высоты.
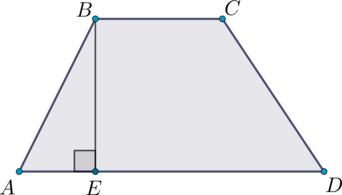
Площадь трапеции равна произведению полусуммы оснований на высоту. Полусумма оснований трапеции \(ABCD\) равна \(0,5(5 + 2\cdot 5) = 7,5\). Площадь трапеции \(ABCD\) равна \(7,5 BE\), тогда \(\dfrac{S_{ABCD}}{BE} = 7,5\).
В трапеции \(ABCD\) с основаниями \(BC = 3\) и \(AD > BC\) проведены высоты \(BE\) и \(CF\). \(BE\) пересекает среднюю линию \(MN\) в точке \(K\). Известно, что \(MK = 1\), \(DF = 2,4\), \(BF = 5\). Найдите площадь трапеции \(ABCD\).
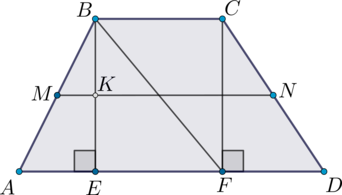
Площадь трапеции равна произведению полусуммы оснований на высоту. Так как \(BC \parallel AD\), то в \(BCFE\) все углы прямые, следовательно, \(BCFE\) – прямоугольник и \(EF = BC = 3\). Средняя линия в трапеции параллельна её основаниям, тогда \(MK \parallel AE\). При этом, \(M\) – середина \(AB\), значит, \(MK\) – средняя линия в треугольнике \(ABE\). Средняя линия треугольника равна половине его основания, тогда \(AE = 2\cdot MK = 2\).
\(AD = AE + EF + FD = 2 + 3 + 2,4 = 7,4\). Треугольник \(BCF\) – прямоугольный. \(BC = 3\), \(BF = 5\), откуда по теореме Пифагора: \(CF^2 = BF^2 - BC^2 = 25 - 9 = 16\), то есть, \(CF = 4\).
Площадь \(ABCD\) равна \(0,5(3 + 7,4)\cdot 4 = 20,8\).
Основания \(AD\) и \(BC\) трапеции \(ABCD\) равны соответственно \(20\) и \(12\), одна из боковых сторон равна \(10\), площадь трапеции \(ABCD\) равна \(80\). Найдите острый угол трапеции \(ABCD\), который образует эта боковая сторона с одним из оснований. Ответ дайте в градусах.

Пусть \(AB = 10\), \(BE\) – перпендикуляр к \(AD\), точка \(E\) лежит на \(AD\).
Площадь трапеции равна произведению полусуммы оснований на высоту, тогда \(80 = 0,5(20 + 12)\cdot BE\).
\(BE = 5 = 0,5\cdot AB\). Треугольник \(ABE\), – прямоугольный, причём \(BE = 0,5\cdot AB\), тогда угол, лежащий против катета \(BE\), равен \(30^{\circ}\).
\(\angle BAE = 30^{\circ}\) – единственный острый угол трапеции \(ABCD\), который образует \(AB\) с одним из оснований.


