Площадь треугольника
Готовиться с нами - ЛЕГКО!

Боковая сторона равнобедренного треугольника равна \(5\), а основание равно \(6\). Найдите площадь этого треугольника.
Проведем высоту к основанию. В равнобедренном треугольнике высота, проведенная к основанию, является и медианой.
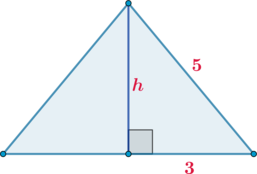
Таким образом мы получили прямоугольный треугольник с катетами \(h\) и \(3\) и гипотенузой \(5\). По теореме Пифагора найдем \(h=\sqrt{5^2-3^2}=4\) (заметим, что такой треугольник называется “египетским”).
Так как площадь треугольника равна половине произведения высоты на основание, к которому она проведена, то \[S=\dfrac12 h\cdot 6=12\]
У треугольника со сторонами \(9\) и \(6\) проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна \(4\). Чему равна высота, проведенная ко второй стороне?
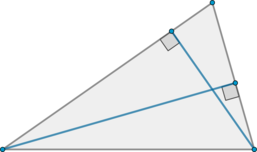
Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне. Следовательно, с одной стороны, \(S=0,5\cdot 9\cdot 4\), а с другой стороны \(S=0,5\cdot 6\cdot h\), где \(h\) – высота, которую нужно найти. Следовательно, \[0,5\cdot 9\cdot 4=0,5\cdot 6\cdot h\quad\Leftrightarrow\quad h=6\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(30^\circ\). Боковая сторона треугольника равна \(10\). Найдите площадь этого треугольника.

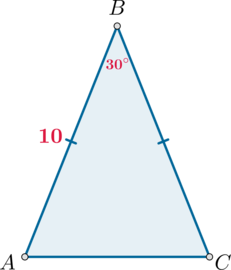
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 10^2 \cdot \dfrac12=25\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(150^\circ\). Боковая сторона треугольника равна \(20\). Найдите площадь этого треугольника.

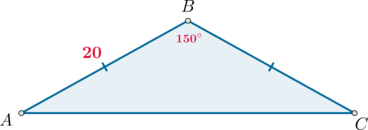
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 20^2 \cdot \dfrac12=100\]
Найдите площадь треугольника, две стороны которого равны \(8\) и \(12\), а угол между ними равен \(30^\circ\).
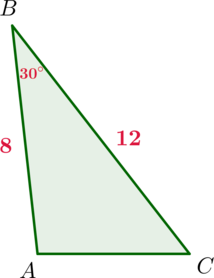
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 8\cdot 12 \cdot \dfrac12=24\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(30^\circ\). Найдите боковую сторону этого треугольника, если его площадь равна \(25\).

Пусть \(a\) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[\dfrac12\cdot a^2\cdot \sin30^\circ=S=25\quad\Rightarrow\quad
a^2=100\quad\Rightarrow\quad a=10\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(150^\circ\). Найдите боковую сторону этого треугольника, если его площадь равна \(100\).

Пусть \(a\) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[\dfrac12\cdot a^2\cdot \sin30^\circ=S=100\quad\Rightarrow\quad
a^2=400\quad\Rightarrow\quad a=20\]



