Решение задач с буквенными выражениями
Готовиться с нами - ЛЕГКО!

На координатной прямой отмечено число \(q\).

Какое утверждение относительно этого числа является верным?
1) \(q+2>0\quad \) 2) \(8-q<0\quad \) 3) \(q+5>0\quad \) 4) \(q+7<0\)
Из рисунка следует, что \(-4<q<-3\). Следовательно, \(-2<q+2<-1\), \(11<8-q<12\), \(1<q+5<2\), \(3<q+7<4\). Следовательно, из всех утверждений верным будет утв. 3.
(Подсказка: в таких заданиях можно по рисунку определить приблизительное значение данного числа, например, \(q\approx -3,6\) и вычислить значения выражений из пунктов 1-4 для числа \(-3,6\).)
На координатной прямой отмечено число \(a\).

Какое утверждение относительно этого числа является верным?
1) \(a-5>0\quad \) 2) \(a-4<0\quad \) 3) \(5-a>0\quad \) 4) \(4-a>0\)
Из рисунка следует, что \(4<a<5\). Следовательно, \(-1<a-5<0\), \(0<a-4<1\), \(0<5-a<1\), \(-1<4-a<0\). Следовательно, верным утверждением будет утв. 3.
(Подсказка: в таких заданиях можно по рисунку определить приблизительное значение данного числа, например, \(a\approx 4,6\) и вычислить значения выражений из пунктов 1-4 для числа \(4,6\).)
На координатной прямой отмечены числа \(a, b, c\).

Какая из разностей \(a-b\), \(a-c\), \(c-b\) положительна?
1) \(a-b\quad \) 2) \(a-c\quad \) 3) \(c-b\quad \) 4) ни одна из них
Из рисунка можно сделать вывод, что \(0<a<b<c\). Следовательно, \(a-b<0\), \(a-c<0\), \(c-b>0\). Таким образом, ответ 3.
(Подсказка: в таких заданиях можно по рисунку определить приблизительные значения данных чисел, например, \(a\approx 1,2\), \(b\approx 2,7\), \(c\approx 3,4\) и вычислить значения выражений из пунктов 1-4 для этих чисел.)
На координатной прямой отмечены числа \(a, b, c\).

Какая из разностей \(a-b\), \(a-c\), \(c-b\) положительна?
1) \(a-b\quad \) 2) \(a-c\quad \) 3) \(c-b\quad \) 4) ни одна из них
Из рисунка можно сделать вывод, что \(a<c<b\), причем \(a<0\), \(b, c>0\). Следовательно, \(a-b<0\), \(a-c<0\), \(c-b<0\). Таким образом, ответ 4.
(Подсказка: в таких заданиях можно по рисунку определить приблизительные значения данных чисел, например, \(a\approx -0,5\), \(b\approx 4,3\), \(c\approx 2,4\) и вычислить значения выражений из пунктов 1-4 для этих чисел.)
На координатной прямой отмечены числа \(a, b, c\).
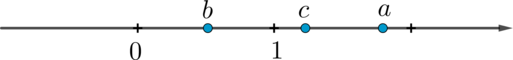
Какая из разностей \(a-b\), \(a-c\), \(c-b\) отрицательна?
1) \(a-b\quad \) 2) \(a-c\quad \) 3) \(c-b\quad \) 4) ни одна из них
Из рисунка можно сделать вывод, что \(b<c<a\). Следовательно, \(a-b>0\), \(a-c>0\), \(c-b>0\). Таким образом, ответ 4.
(Подсказка: в таких заданиях можно по рисунку определить приблизительные значения данных чисел, например, \(a\approx 1,8\), \(b\approx 0,5\), \(c\approx 1,3\) и вычислить значения выражений из пунктов 1-4 для этих чисел.)
На координатной прямой отмечены числа \(a, b\).
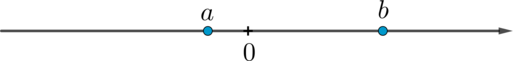
Какое из приведенных утверждений для этих чисел неверно?
1) \(a+b>0\quad \) 2) \(a-b<0\quad \) 3) \(ab>0\quad \) 4) \(ab^2<0\)
Из рисунка следует, что \(a<0\), \(b>0\), причем, так как число \(b\) находится от нуля дальше, чем число \(a\), то \(|b|>|a|\). Для удобства можно взять любые два числа, удовлетворяющие этим условиям, например, \(a=-1\), \(b=4\). Проверяем: \(a+b=3>0\), \(a-b=-5<0\), \(ab=-4<0\), \(ab^2=-16<0\). Следовательно, неверным будет пункт 3.
На координатной прямой отмечены числа \(x, y\).
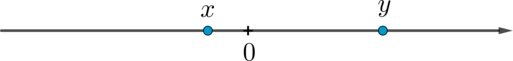
Какое из приведенных утверждений для этих чисел неверно?
1) \(y-x<0\quad \) 2) \(x^2y>0\quad \) 3) \(xy<0\quad \) 4) \(x+y>0\)
Из рисунка следует, что \(x<0\), \(y>0\), причем, так как число \(y\) находится от нуля дальше, чем число \(x\), то \(|y|>|x|\). Для удобства можно взять любые два числа, удовлетворяющие этим условиям, например, \(x=-1\), \(y=3\). Проверяем: \(y-x=4>0\), \(x^2y=3>0\), \(xy=-3<0\), \(x+y=2>0\). Следовательно, неверным будет пункт 1.



