Решение задач с числовой прямой и промежутками на прямой (страница 2)
Готовиться с нами - ЛЕГКО!

Одно из чисел \(\dfrac27, \dfrac47, \dfrac{10}7, \dfrac{11}7\) отмечено на прямой точкой.
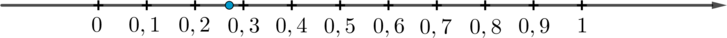
Какое это число?
1) \(\dfrac27\qquad \) 2) \(\dfrac47\qquad \) 3) \(\dfrac{10}7\qquad \) 4) \(\dfrac{11}7\)
Из рисунка видно, что точка находится на отрезке \([0,2;0,3]\). Если записать \(0,2=\frac{0,2}1=\frac{1,4}7\), \(0,3=\frac{2,1}7\), то видно, что между этими числами находится число \(\frac27\). Следовательно, ответ 1.
На координатной прямой точки \(A, B, C\) и \(D\) соответствуют числам \(0,0137\); \(0,103\); \(0,03\); \(0,021\).

Какой точке соответствует число \(0,03\)?
1) точка \(A\qquad \) 2) точка \(B\qquad \) 3) точка \(C\qquad \) 4) точка \(D\)
Упорядочим данные числа по возрастанию.
Если записать \(0,0137; \ 0,1030; \ 0,0300; \ 0,0210\), то: \[0,0137<0,0210<0,0300<0,1030\]
Следовательно, число \(0,03\) третье по порядку, значит, соответствует точке \(C\). Ответ 3.
На координатной прямой точки \(A, B, C\) и \(D\) соответствуют числам \(0,1032\); \(-0,031\); \(-0,01\); \(-0,104\).

Какой точке соответствует число \(-0,031\)?
1) точка \(A\qquad \) 2) точка \(B\qquad \) 3) точка \(C\qquad \) 4) точка \(D\)
Упорядочим данные числа по возрастанию. Заметим, что среди данных чисел единственное положительное число – это \(0,1032\), следовательно, оно будет наибольшим. Упорядочим отрицательные по возрастанию. Если записать \(-0,031; \ -0,010; \ -0,104\), то: \[-0,104< -0,031< -0,010<0,1032\]
Следовательно, число \(-0,031\) второе по порядку, значит, соответствует точке \(B\). Ответ 2.
На координатной прямой точками отмечены числа \(\frac{1}{7}\); \(\frac{1}{8}\); \(\frac{2}{5}\) и \(0,8\).
 Какому числу соответствует точка С?
Какому числу соответствует точка С?
1) \(\frac{1}{7}\) \(\;\;\;\) 2)\(\frac{1}{8}\) \(\;\;\;\) 3)\(\frac{2}{5}\) \(\;\;\;\) 4)\(0,8\)
Преведем первые 3 дроби к одному числителю 2. Получим:
\[\frac{2}{14}; \; \frac{2}{16}; \; \frac{2}{5}.\]
Из дробей с одинаковым числителем больше та, у которой меньше знаменатель. Значит:
\[\frac{2}{16}< \frac{2}{14} < \frac{2}{5}.\]
Представим десятичную дробь в виде обыкновенной \[0,8 = \frac{8}{10}=\frac{4}{5} > \frac{2}{5}.\]
Точка С соответствует числу \(\frac{2}{5}\).
На координатной прямой точками отмечены числа \(\frac{4}{3}\); \(\frac{7}{5}\); \(1,25\) и \(1,08\).
 Какому числу соответствует точка B?
Какому числу соответствует точка B?
1) \(\frac{4}{3}\) \(\;\;\;\) 2)\(\frac{7}{5}\) \(\;\;\;\) 3)\(1,25\) \(\;\;\;\) 4)\(1,08\)
Представим все дроби в виде обыкновенных и приведем их к одинаковому знаменателю.
\[1,25 = \frac{125}{100}=\frac{5}{4},\] \[1,08 = \frac{108}{100}=\frac{27}{25}.\]
Наименьший общий знаменатель в данном случае равен \(3 \cdot 25 \cdot 4 = 300\). \[\frac{27}{25}=\frac{324}{300} < \frac{5}{4}=\frac{375}{300} < \frac{4}{3}=\frac{400}{300} < \frac{7}{5}=\frac{420}{300}\]
Вторым по возрастанию является число 1,25.
На координатной прямой отмечена одна из точек \(\frac{2}{21}; \frac{4}{21}; \frac{5}{21}; \frac{10}{21}\).
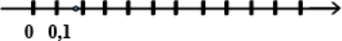
Какая это точка?
1) \(\frac{2}{21}\) \(\;\;\;\) 2)\(\frac{4}{21}\) \(\;\;\;\) 3)\(\frac{5}{21}\) \(\;\;\;\) 4)\(\frac{10}{21}\)
Заметим, что отмеченная точка лежит на отрезке \([0,1;0,2]\) или \([\frac{2,1}{21};\frac{4,2}{21}]\). Значит, это точка \(\frac{4}{21}\).
На координатной прямой отмечена одна из точек \(\frac{3}{17}; \frac{7}{17}; \frac{9}{17}; \frac{10}{17}\).
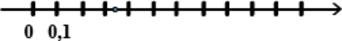
Какая это точка?
1) \(\frac{3}{17}\) \(\;\;\;\) 2)\(\frac{7}{17}\) \(\;\;\;\) 3)\(\frac{9}{17}\) \(\;\;\;\) 4)\(\frac{10}{17}\)
Заметим, что отмеченная точка лежит на отрезке \([0,4;0,5]\) или \([\frac{6,8}{17};\frac{8,5}{17}]\). Значит, это точка \(\frac{7}{17}\).



