Нахождение приближенного значения рационального числа
Готовиться с нами - ЛЕГКО!

На координатной прямой отмечены точки \(A, B, C, D\).

Одна из них соответствует числу \(\dfrac{58}7\). Какая это точка?
1) точка \(A\qquad \) 2) точка \(B\qquad \) 3) точка \(C\qquad \) 4) точка \(D\)
Выделим целую часть: \(\frac{58}7=8\,\frac27\). Следовательно, это число находится между числами \(8\) и \(9\), но левее \(8,5\) (то есть левее середины отрезка \([8;9]\)). Значит, это точка \(C\). Ответ 3.
На координатной прямой отмечены точки \(A, B, C, D\).

Одна из них соответствует числу \(\dfrac{63}{11}\). Какая это точка?
1) точка \(A\qquad \) 2) точка \(B\qquad \) 3) точка \(C\qquad \) 4) точка \(D\)
Выделим целую часть: \(\frac{63}{11}=5\,\frac8{11}\). Следовательно, это число находится между числами \(5\) и \(6\), но правее \(5,5\) (то есть правее середины отрезка \([5;6]\)). Значит, это точка \(B\). Ответ 2.
Какое из данных чисел принадлежит отрезку \([7;8]\)?
1) \(\dfrac{69}{11}\qquad \) 2) \(\dfrac{80}{11}\qquad \) 3) \(\dfrac{90}{11}\qquad \) 4) \(\dfrac{92}{11}\)
Приведем числа \(7\) и \(8\) к знаменателю \(11\): \(7=\frac{77}{11}\), \(8=\frac{88}{11}\). Следовательно, между ними находится число из пункта 2.
Какое из данных чисел принадлежит отрезку \([5;6]\)?
1) \(\dfrac{49}{15}\qquad \) 2) \(\dfrac{52}{15}\qquad \) 3) \(\dfrac{58}{15}\qquad \) 4) \(\dfrac{71}{15}\)
Приведем числа \(5\) и \(6\) к знаменателю \(15\): \(5=\frac{75}{15}\), \(6=\frac{80}{15}\). Следовательно, между ними находится число из пункта 4.
Одно из чисел \(\dfrac{33}7, \, \dfrac{37}7, \ \dfrac{41}7, \ \dfrac{43}7\) отмечено на прямой точкой.
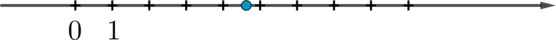
Какое это число?
1) \(\dfrac{33}7\qquad \) 2) \(\dfrac{37}7\qquad \) 3) \(\dfrac{41}7\qquad \) 4) \(\dfrac{43}7\)
Из рисунка видно, что точка находится на отрезке \([4;5]\). Если записать \(4=\frac{28}7\), \(5=\frac{35}7\), то видно, что между этими числами находится число \(\frac{33}7\). Следовательно, ответ 1.
Одно из чисел \(\dfrac{58}{13}, \dfrac{69}{13}, \dfrac{76}{13},
\dfrac{83}{13}\) отмечено на прямой точкой.

Какое это число?
1) \(\dfrac{58}{13}\qquad \) 2) \(\dfrac{69}{13}\qquad \) 3) \(\dfrac{76}{13}\qquad \) 4) \(\dfrac{88}{13}\)
Из рисунка видно, что точка находится на отрезке \([5;6]\). Если записать \(5=\frac{65}{13}\), \(6=\frac{78}{13}\), то видно, что между этими числами находится число \(\frac{76}{13}\). Следовательно, ответ 3.
Одно из чисел \(\dfrac59, \dfrac{11}9, \dfrac{13}9, \dfrac{14}9\) отмечено на прямой точкой.

Какое это число?
1) \(\dfrac59\qquad \) 2) \(\dfrac{11}9\qquad \) 3) \(\dfrac{13}9\qquad \) 4) \(\dfrac{14}9\)
Из рисунка видно, что точка находится на отрезке \([0,5;0,6]\). Если записать \(0,5=\frac{0,5}1=\frac{4,5}9\), \(0,6=\frac{5,4}9\), то видно, что между этими числами находится число \(\frac59\). Следовательно, ответ 1.



