Задачи на клетчатой бумаге
Готовиться с нами - ЛЕГКО!

Найдите радиус окружности, вписанной в треугольник \(ABC\), считая стороны квадратных клеток равными \(1\).
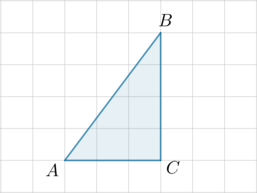
Так как радиус окружности, вписанной в прямоугольный треугольник, ищется по формуле \(r=(a+b-c):2\), где \(a, b\) – катеты, \(c\) – гипотенуза, то \[r=\dfrac{3+4-\sqrt{3^2+4^2}}2=1\]
Найдите угол \(ABC\). Ответ дайте в градусах.

Пусть \(O\) – центр окружности.
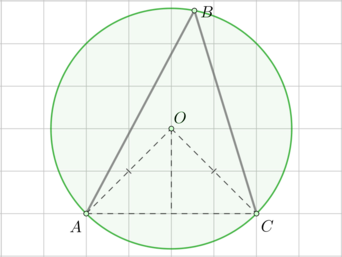
Пусть сторона клетки равна \(1\). Точки \(O\), \(C\) и \(A\) находятся в узлах решетки, причем \(AO\) – гипотенуза равнобедренного прямоугольного треугольника с катетами \(2\), следовательно, \(AO=2\sqrt2\). \(AO=CO\) – радиусы окружности. \(AC=4\).
Заметим, что \(AO^2+CO^2=AC^2\), следовательно, по обратной теореме Пифагора, \(\angle AOC=90^\circ\). Это центральный угол, опирающийся на хорду \(AC\). Тогда вписанный угол \(ABC\), опирающийся на эту же хорду, равен половине \(\angle AOC\), то есть \(45^\circ\).
Найдите градусную меру дуги \(AC\) окружности, на которую опирается угол \(ABC\). Ответ дайте в градусах.

Пусть \(O\) – центр окружности.
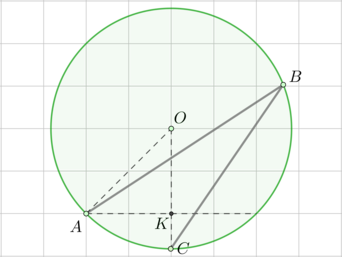
Пусть сторона клетки равна \(1\). Точки \(O\) и \(A\) находятся в узлах решетки, причем \(AO\) – гипотенуза равнобедренного прямоугольного треугольника \(AOK\) (с катетами \(2\)). Следовательно, \(\angle AOK=\angle OAK=45^\circ\).
\(\angle AOC=\angle AOK=45^\circ\) – центральный угол, опирающийся на хорду \(AC\). Тогда градусная мера дуги \(AC\) также равна \(45^\circ\).
На клетчатой бумаге с размером клетки \(1\times 1\) изображен угол. Найдите синус этого угла.
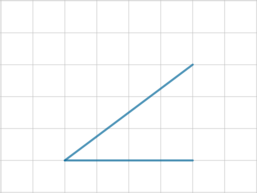
Отметим точки \(A, B, C\), проведем отрезок \(BC\):
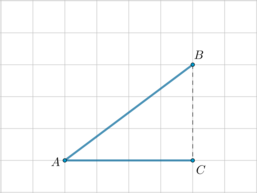
Заметим, что все вершины треугольника \(ABC\) находятся в узлах решетки, причем \(AC=4, BC=3\). Тогда \(AB=\sqrt{3^2+4^2}=5\). Так как синус острого угла (в прямоугольном треугольнике) – это отношение противолежащего катета к гипотенузе, то \[\sin \angle A=\dfrac{BC}{AB}=\dfrac35=0,6\]
На клетчатой бумаге с размером клетки \(1\times 1\) изображен угол. Найдите синус этого угла.
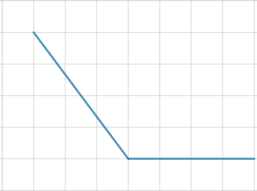
Продлим одну из сторон тупого угла \(A\) на отрезок \(AC\) так, чтобы \(BC\perp
AC\):
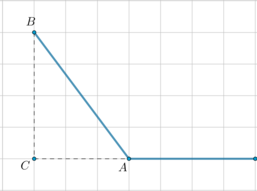
Заметим, что все вершины треугольника \(ABC\) находятся в узлах решетки, причем \(AC=3, BC=4\). Тогда \(AB=\sqrt{3^2+4^2}=5\). Так как синус острого угла (в прямоугольном треугольнике) – это отношение противолежащего катета к гипотенузе, то \[\sin \angle BAC=\dfrac{BC}{AB}=\dfrac45=0,8\] Угол \(BAC\) с тупым углом \(A\) – смежные, следовательно, их синусы равны, значит, синус тупого угла \(A\) равен также \(0,8\).
На клетчатой бумаге с размером клетки \(1\times 1\) изображен угол. Найдите косинус этого угла.
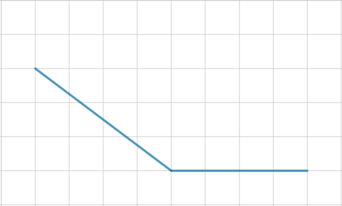
Продлим одну из сторон тупого угла \(A\) на отрезок \(AC\) так, чтобы \(BC\perp
AC\):
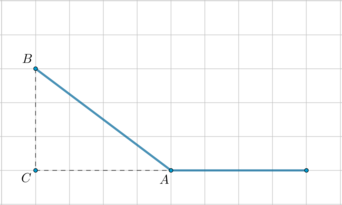
Заметим, что все вершины треугольника \(ABC\) находятся в узлах решетки, причем \(AC=4, BC=3\). Тогда \(AB=\sqrt{3^2+4^2}=5\). Так как косинус острого угла (в прямоугольном треугольнике) – это отношение прилежащего катета к гипотенузе, то \[\cos \angle BAC=\dfrac{AC}{AB}=\dfrac45=0,8\] Угол \(BAC\) с тупым углом \(A\) – смежные, следовательно, их косинусы противоположны, значит, косинус тупого угла \(A\) равен \(-0,8\).
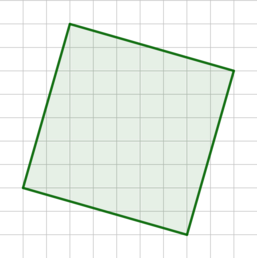
Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки \(1\) см \(\times\) \(1\) см. Ответ дайте в квадратных сантиметрах.
Рассмотрим прямоугольный \(\triangle ANL\):
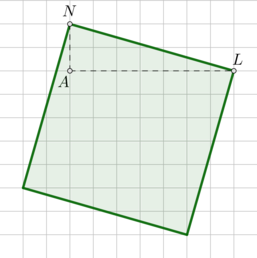
Все точки \(A, N, L\) лежат в узлах решетки, \(NL\) – гипотенуза этого треугольника и сторона квадрата. Так как площадь квадрата равна квадрату его стороны, то \[S=NL^2=AN^2+AL^2=2^2+7^2=53\]



