Задачи по теме «Конус»
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Точка \(P\) – вершина конуса.
\(\blacktriangleright\) Отрезок, соединяющий вершину конуса с границей основания, называется образующей (все образующие равны между собой).
\(\blacktriangleright\) Отрезок, соединяющий вершину конуса с центром основания-круга, является высотой конуса.
\(\blacktriangleright\) Площадь боковой поверхности конуса \({\large{S_{\text{бок.пов.}}=\pi rl}}\), где \(r\) – радиус основания, \(l\) – образующая.
\(\blacktriangleright\) Площадь полной поверхности конуса – эта сумма площади боковой поверхности и площади основания. \[{\large{S_{\text{полн.пов.}}=\pi rl+\pi r^2=\pi r(r+l)}}\]
\(\blacktriangleright\) Объем конуса \({\large{V=\dfrac{1}{3}S_{\text{осн.}}\cdot h=\dfrac{1}{3}\pi
r^2h}}\), где \(h\) – высота конуса.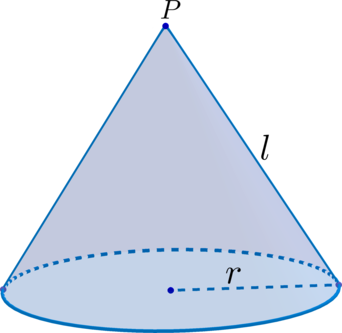
Заметим, что конус имеет некоторое сходство с пирамидой, только в основании пирамиды лежит многоугольник (граница которого – ломаная), а в основании конуса – круг (граница которого – гладкая).
Поэтому можно сказать, что поверхность пирамиды “ребристая” , а конуса – “гладкая”.
Площадь боковой поверхности конуса равна \(48\pi\), а площадь основания равна \(36\pi\). Найдите длину образующей конуса.
Если радиус окружности, лежащей в основании конуса обозначить за \(r\), а длину образующей за \(l\), то площадь основания и площадь боковой поверхности конуса выразятся по формулам: \(S_{\text{осн.}} = \pi r^2\), \(S_{\text{бок.пов.}} = \pi r l\). Из первой формулы следует: \(\pi r^2 = 36\pi\) \(\Rightarrow\) \(r^2 = 36\) \(\Rightarrow\) \(r = 6\) \(\Rightarrow\) \(6\pi l = 48\pi\) \(\Rightarrow\) \(6l = 48\) \(\Rightarrow\) \(l = 8\).
Площадь боковой поверхности конуса равна \(48\pi\), а площадь боковой поверхности усеченного конуса с такими же основанием и углом наклона образующей к плоскости основания равна \(36\pi\). Найдите высоту усеченного конуса, если высота исходного конуса равна \(10\).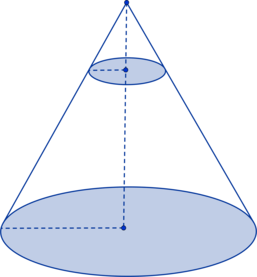
Площадь боковой поверхности меньшего конуса, который дополняет усеченный конус до полного, равна разности их площадей поверхностей: \(S_{\text{мал}} = 48\pi - 36\pi = 12\pi\). Отношение площадей боковых поверхностей большого и малого конусов равно квадрату коэффициента подобия между ними: \[\frac{S_{\text{бол}}}{S_{\text{мал}}} = k^2 =
\frac{48\pi}{12\pi} = 4\Rightarrow k = 2\]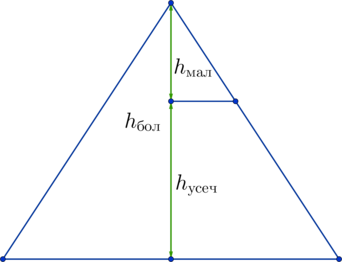
Тогда высоты конусов относятся друг к другу: \(\dfrac{h_{\text{бол}}}{h_{\text{мал}}} = \dfrac{10}{h_{\text{мал}}} = k = 2\). Тогда
\[h_{\text{мал}} = 5\Rightarrow h_{\text{усеч}} = h_{\text{бол}} - h_{\text{мал}} = 10 - 5 = 5\]
На высоте конуса с вершиной \(A\), центром основания \(C\) и радиусом основания \(R = 4\) отметили точку \(E\) такую, что расстояние от неё до основания равно \(\sqrt{3}(4-\pi^{-0,5})\). Известно, что угол между образующей конуса и плоскостью основания равен \(60^\circ\). Найдите площадь сечения \(T\) конуса, проходящего через точку \(E\) и параллельного основанию конуса.
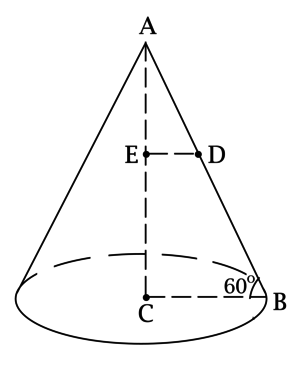
Рассмотрим треугольник \(ABC\), где \(B\) – некоторая точка на окружности основания. Так как \(AC\) – высота конуса, то \(AC\perp CB\), тогда \(\angle CAB = 90^\circ - \angle ABC = 30^\circ\), следовательно, \(AB = 2CB = 8\). По теореме Пифагора \[AC = \sqrt{AB^2 - CB^2} = 4\sqrt{3}.\]
Обозначим через \(D\) точку пересечения плоскости сечения \(T\) и \(AB\). Рассмотрим треугольник \(AED\): \[AE = AC - CE = 4\sqrt{3} - \sqrt{3}(4 - \pi^{-0,5}) = \sqrt{\dfrac{3}{\pi}}.\]
Так как сечение \(T\) параллельно плоскости основания, а \(AC\) – высота конуса, то \(AC\perp ED\), тогда \(\triangle AED\) – прямоугольный и \(\angle EAD = 30^\circ\), откуда \[ED = AE\cdot \mathrm{tg}\, \angle EAD = \sqrt{\dfrac{3}{\pi}}\cdot \dfrac{1}{\sqrt{3}} = \dfrac{1}{\sqrt{\pi}} = r\] – радиус сечения \(T\).
Таким образом, площадь сечения \(T\) равна \(\pi r^2 = \pi\cdot\dfrac{1}{\pi} = 1\).
Радиусы оснований усечённого конуса равны \[r = \dfrac{2}{\sqrt[4]{2}\sqrt{\pi}}\qquad \text{и}\qquad R = \dfrac{10}{\sqrt[4]{2}\sqrt{\pi}},\] а угол между его образующей и основанием равен \(45^\circ\). Найдите площадь боковой поверхности этого усечённого конуса.
Обозначим центры оснований усечённого конуса через \(A\) и \(E\), так что \(A\) – центр большего основания. Отметим на большем основании точку \(C\), а точку меньшего основания, через которую проходит образующая, выходящая из \(C\), обозначим через \(D\).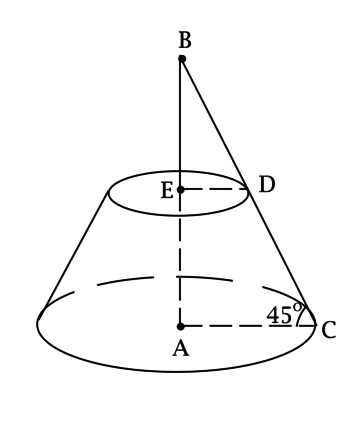
Высота \(AE\) и образующая \(CD\) лежат в одной плоскости. Обозначим точку их пересечения через \(B\).
Так как \(AE\) – высота, то \(AE\perp CD\) и \(AE\perp AC\).
Рассмотрим прямоугольный треугольник \(BAC\):
в нём \(\angle BCA = 45^\circ\), тогда \[AB = R = \dfrac{10}{\sqrt[4]{2}\sqrt{\pi}},\qquad\qquad BC = R\sqrt{2} = \dfrac{10\sqrt{2}}{\sqrt[4]{2}\sqrt{\pi}}.\]
Рассмотрим прямоугольный треугольник \(BED\):
так как \(\angle EBD = 45^\circ\), то \[BE = r = \dfrac{2}{\sqrt[4]{2}\sqrt{\pi}},\qquad\qquad BD = r\sqrt{2} = \dfrac{2\sqrt{2}}{\sqrt[4]{2}\sqrt{\pi}},\] тогда \(EA = AB - BE = R - r\), \(DC = BC - BD = R\sqrt{2} - r\sqrt{2} = \sqrt{2}(R - r)\). \[S_{\text{бок}} = \pi(R + r)\cdot I,\] где \(I\) – образующая, тогда \[S_{\text{бок}} = \pi(R + r)\cdot\sqrt{2}(R - r) = \sqrt{2}\pi(R^2 - r^2) = \sqrt{2}\pi\left(\dfrac{100}{\sqrt{2}\pi} - \dfrac{4}{\sqrt{2}\pi}\right) = 96.\]
Старшеклассникам, которые готовятся к сдаче ЕГЭ по математике, непременно стоит научиться вычислять площадь и другие неизвестные параметры конуса. Как показывает практика предыдущих лет, подобные задания из раздела «Геометрия в пространстве» вызывают у выпускников определенные сложности.
При этом понимать, как найти площадь боковой поверхности или, к примеру, сечения конуса, параллельного основанию, должны все учащиеся, независимо от уровня их подготовки. Это позволит им успешно пройти аттестационное испытание по математике.
Базовая информация, которую стоит запомнить
- Конус представляет собой геометрическое тело, которое образовано совокупностью круга, точки, находящейся вне его плоскости, и лучей, соединяющих заданную точку с точками круга. Его высотой называется перпендикуляр, который опущен из вершины на плоскость основания.
- Все образующие конуса равны между собой.
- Осевое сечение конуса представляет собой равнобедренный треугольник. Основание этой фигуры равняется двум радиусам. Боковые стороны треугольника равны образующим конуса.
Занимайтесь вместе с сайтом «Школково»!
Чтобы не допускать распространенных ошибок при решении задач по теме «Конус», выбирайте наш математический портал. Здесь есть весь необходимый материал для изучения разделов, требующих повторения.
Специалисты образовательного проекта «Школково» предлагают новый подход к подготовке к экзамену, предполагающий переход от простого к сложному. Вначале мы даем полную теорию, основные формулы и элементарные практические задачи с решением, в том числе и по теме «Конус», а затем постепенно переходим к заданиям экспертного уровня, которые также встречаются в ЕГЭ. Вся необходимая информация представлена в разделе «Теоретическая справка».
Вы также можете сразу приступить к решению онлайн-задач на вычисление высоты усеченного конуса, площади его боковой поверхности, объема, а также похожих задач на вычисление, например, нахождению объема или площади сечения куба. Большая база упражнений представлена в разделе «Каталог». Перечень заданий систематически обновляется.
Проверьте, насколько легко вы сможете определить площадь конуса в режиме онлайн. Если упражнение потребовало от вас минимальных усилий, рекомендуем вам не тратить время на простые задачи и переходить к более сложным. А если затруднения все же возникли, тогда вам непременно стоит находить время в своем ежедневном расписании на дистанционные занятия вместе со «Школково». С нами вы сможете быстро усвоить алгоритм решения задач на расчет объема конуса и других неизвестных параметров.


