Нахождение угла между прямыми
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Угол между прямыми – это такой угол \(\alpha\), что \(0\leqslant \alpha\leqslant 90^\circ\).
\(\blacktriangleright\) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
\(\blacktriangleright\) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.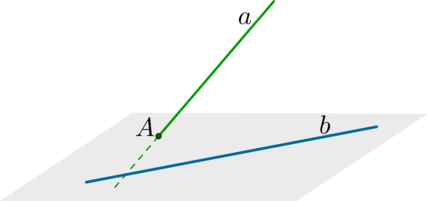
\(\blacktriangleright\) Порядок нахождения угла между скрещивающимися прямыми:
Шаг 1: через одну из двух прямых \(a\) провести плоскость, параллельную второй прямой \(b\) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую \(c\), параллельную прямой \(b\);
Шаг 3: тогда угол между прямыми \(a\) и \(b\) будет равен углу между прямыми \(a\) и \(c\).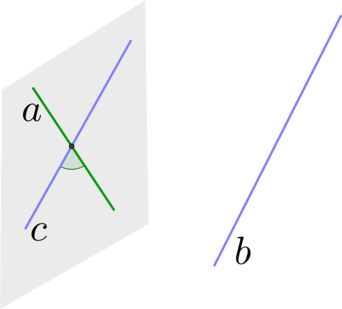
\(ABCDA_1B_1C_1D_1\) – куб. Найдите угол между прямыми, содержащими отрезки \(AC\) и \(B_1D_1\). Ответ дайте в градусах.
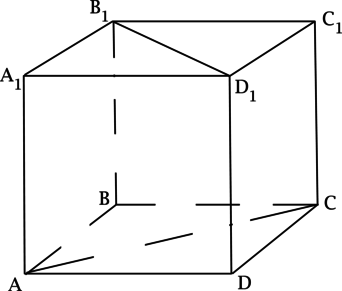
Прямая \(BD\) параллельна прямой \(B_1D_1\), тогда угол между \(AC\) и \(B_1D_1\) равен углу между \(AC\) и \(BD\), но \(AC\) и \(BD\) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ \(90^{\circ}\).
Дана правильная треугольная пирамида \(SABC\) с вершиной \(S\). Найдите угол между высотой пирамиды и ребром \(SB\), если высота пирамиды равна \(2\sqrt3\), а сторона основания пирамиды равна \(6\). Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота \(SO\) падает в точку пересечения медиан основания.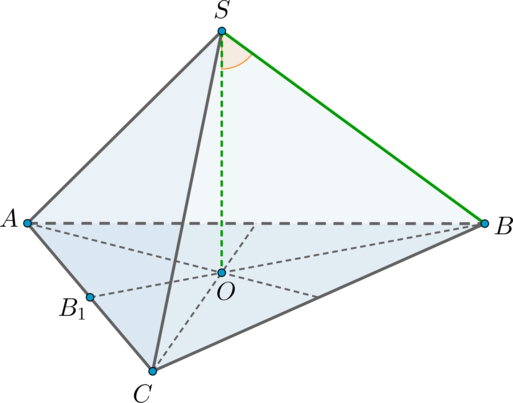
Пусть \(BB_1\) – медиана, а значит, и высота. По теореме Пифагора \[BB_1=\sqrt{BC^2-B_1C^2}=3\sqrt3 \quad\Rightarrow\quad BO=\dfrac23BB_1=2\sqrt3,\] так как медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Следовательно, прямоугольный \(\triangle SOB\) является равнобедренным (\(SO=BO=2\sqrt3\)), значит, острые углы равны по \(45^\circ\).
\(ABCDA_1B_1C_1D_1\) – куб. Точка \(K\) лежит на ребре \(AA_1\). Найдите угол между прямыми, содержащими отрезки \(D_1K\) и \(AB\). Ответ дайте в градусах.
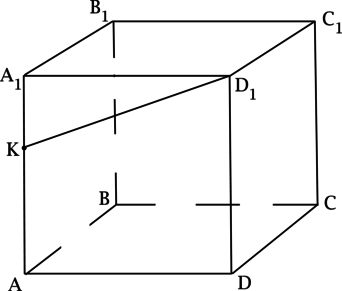
Так как \(ABCDA_1B_1C_1D_1\) – куб, то \(AB\) перпендикулярен плоскости \((ADD_1)\), тогда \(AB\) перпендикулярен любой прямой, лежащей в плоскости \((ADD_1)\), следовательно, угол между прямыми, содержащими отрезки \(D_1K\) и \(AB\) равен \(90^{\circ}\).
Дан правильный тетраэдр \(SABC\). Найдите квадрат тангенса угла между высотой грани \(SAC\), опущенной из вершины \(S\), и высотой грани \(ABC\), опущенной из вершины \(B\).
Пусть \(SB_1\) – высота грани \(SAC\). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть \(SB_1\) также является и медианой, значит, \(AB_1=B_1C\). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если \(SO\) – высота, то \(O\) – точка пересечения медиан треугольника \(ABC\), а значит и высот, так как \(\triangle ABC\) правильный. Следовательно, \(BB_1\) — медиана и высота.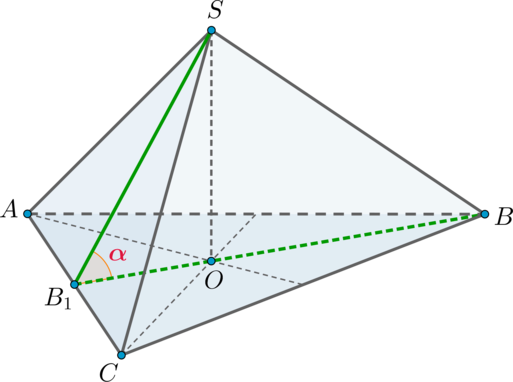
Таким образом, необходимо найти \(\mathrm{tg}^2\angle (SB_1,
BB_1)\).
Пусть \(a\) – ребро тетраэдра. Тогда \(BC=a, B_1C=0,5a\), следовательно, по теореме Пифагора \[BB_1=\sqrt{BC^2-B_1C^2}=\dfrac{\sqrt3}2a\] Так как \(O\) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины, то \(OB_1=\frac13BB_1=\frac{\sqrt3}6a\).
Так как \(\triangle ABC=\triangle SAC\), то \(SB_1=BB_1\). Следовательно, из прямоугольного \(\triangle SB_1O\): \[\cos
\alpha=\dfrac{OB_1}{SB_1}=\dfrac13 \quad\Rightarrow\quad \sin \alpha
=\sqrt{1-\cos^2\alpha}=\dfrac{2\sqrt2}3 \quad\Rightarrow\quad
\mathrm{tg}^2\alpha=(2\sqrt2)^2=8.\]
Дан куб \(ABCDA_1B_1C_1D_1\). Найдите угол между прямыми \(AD_1\) и \(BD\). Ответ дайте в градусах.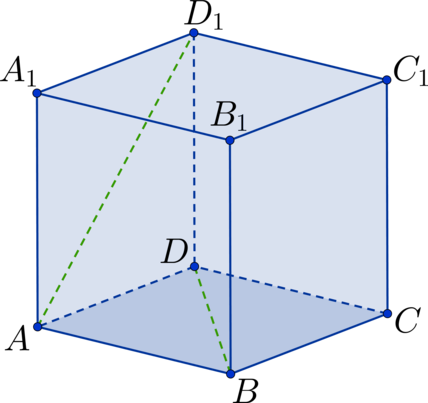
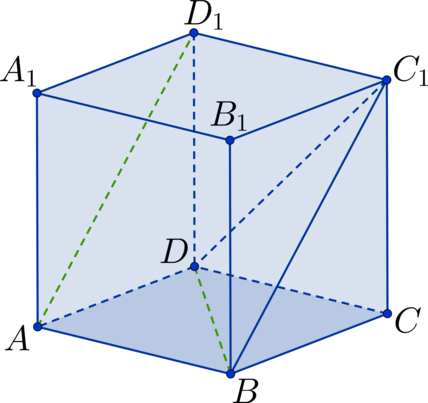
Заметим, что \(BC_1 || AD_1\), тогда рассмотрим треугольник \(\triangle BDC_1\), в котором необходимо определить \(\angle DBC_1\). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали \(\Rightarrow\) \(\triangle BDC_1\) – равносторонний треугольник \(\Rightarrow\) \(\angle DBC_1 = 60^\circ\).
Дан куб \(ABCDA_1B_1C_1D_1\). Точка \(K\) – середина стороны \(B_1C_1\), а точка \(L\) – середина стороны \(C_1D_1\). Найдите угол между прямыми \(AB_1\) и \(KL\). Ответ дайте в градусах.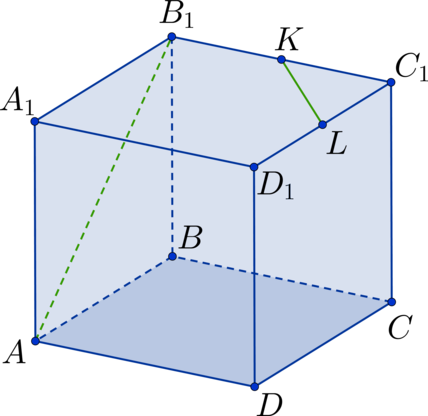
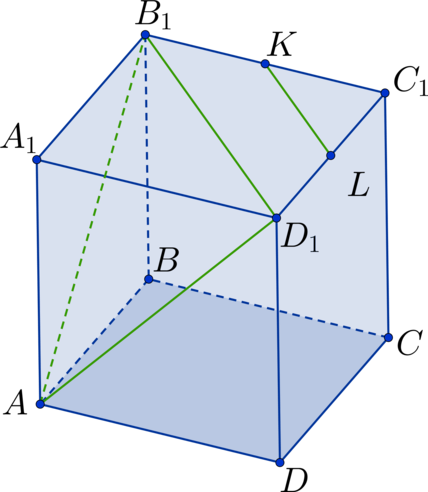
Проведем диагональ \(B_1D_1\) в квадрате \(A_1B_1C_1D_1\). Тогда \(KL\) – средняя линия в \(\triangle B_1C_1D_1\) \(\Rightarrow\) \(KL || B_1D_1\) \(\Rightarrow\) \(\angle AB_1D_1\) – искомый угол. Рассмотрим \(\triangle AB_1D_1\). Он состоит из диагоналей соответствующих квадратов \(\Rightarrow\) треугольник является равносторонним \(\Rightarrow\) \(\angle AB_1D_1 = 60^\circ\).
Дана правильная треугольная пирамида \(SABC\) с вершиной \(S\). Найдите косинус угла между высотой основания \(AA_1\) и ребром \(SC\), если сторона основания равна \(\sqrt3\), а боковое ребро равно \(2\).
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, \(AA_1\) также является и медианой.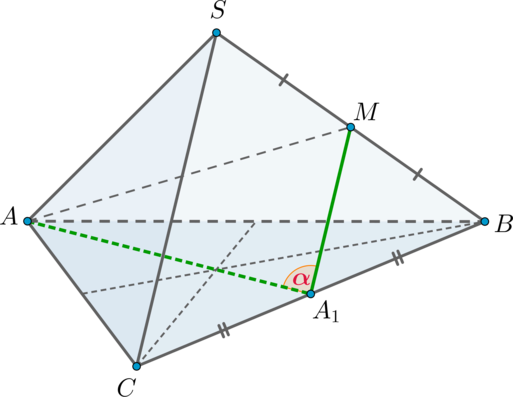
Заметим, что прямые \(AA_1\) и \(SC\) скрещиваются. Проведем \(A_1M\parallel SC\), следовательно, \(\angle (AA_1, SC)=\angle (AA_1,
A_1M)\).
Так как \(A_1M\parallel SC\) и \(A_1\) – середина \(BC\), то \(M\) – середина \(SB\). Следовательно, \(A_1M\) – средняя линия и \[A_1M=\frac12SC=1.\] По теореме Пифагора из \(\triangle ABA_1\): \[AA_1=\sqrt{AB^2-A_1B^2}=\dfrac32.\] Медиану \(AM\) из \(\triangle SAB\) можно найти по формуле медианы: \[AM^2=\dfrac{2AS^2+2AB^2-SB^2}4=\dfrac52.\] Следовательно, по теореме косинусов из \(\triangle AA_1M\): \[\cos \alpha=\dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1\cdot A_1M}=\dfrac14=0,25.\]
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».



