Нетипичные задачи в исследовании функций с помощью производной (страница 2)

\[y' = \ln\dfrac{\pi}{2} \cdot \left(\dfrac{\pi}{2}\right)^x \cos\left(\left(\dfrac{\pi}{2}\right)^x\right).\]

Найдём критические точки: \[\ln\dfrac{\pi}{2} \cdot \left(\dfrac{\pi}{2}\right)^x \cos\left(\left(\dfrac{\pi}{2}\right)^x\right) = 0\qquad\Leftrightarrow\qquad \cos\left(\left(\dfrac{\pi}{2}\right)^x\right) = 0,\] откуда находим: \[\left(\dfrac{\pi}{2}\right)^x = \dfrac{\pi}{2} + \pi k, \ k \in \mathbb{Z}.\]

Среди \(x\) из \([-0,5; 2]\) подходит только \(x = 1\). Проверим, что это точка локального максимума:

при \(-0,5 < x < 1\) имеем \(y' > 0\),

при \(1< x < 2\) имеем \(y' < 0\).

Значит \(x = 1\) – точка локального максимума.

ОДЗ: \(x \neq 0\). Решим на ОДЗ:

1) \[y' = e^x\left(\dfrac{x^2 + 4}{x^3} + \dfrac{2x^4 - 3x^2(x^2 + 4)}{x^6}\right) = \dfrac{e^x}{x^6}(x^5 - x^4 + 4x^3 - 12x^2).\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[\dfrac{e^x}{x^6}(x^5 - x^4 + 4x^3 - 12x^2) = 0\qquad\Leftrightarrow\qquad x^5 - x^4 + 4x^3 - 12x^2 = 0\qquad\Leftrightarrow\qquad x^3 -x^2 + 4x - 12 = 0\] – на ОДЗ. Можно угадать корень \(x = 2\). После деления \(x^3 - x^2 + 4x - 12\) на \((x - 2)\) получим: \[x^2 + x + 6 = (x + 0,5)^2 + 5,75 > 0.\] Производная функции \(y\) не определена при \(x = 0\), но \(x = 0\) не входит в ОДЗ. Таким образом, \[y' = \dfrac{e^x}{x^4}(x - 2)(x^2 + x + 6).\] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):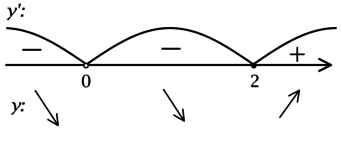



3) Эскиз графика \(y\):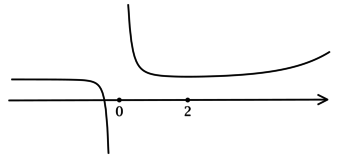



Значит \(x = 2\) – точка локального минимума функции \(y\).

Так как \(e^t\) возрастает, то наибольшее значение \(y\) достигает там же, где и \(\cos (3x) + 2\sin (3x) - \sqrt{5}\).

С помощью формулы для косинуса разности (формула вспомогательного аргумента) можно преобразовать \(\cos (3x) + 2\sin (3x)\) к более удобному виду:

\(\cos (3x) + 2\sin (3x) = \sqrt{5}\left(\dfrac{1}{\sqrt{5}}\cos (3x) + \dfrac{2}{\sqrt{5}}\sin (3x) \right) = \\ = \sqrt{5}\left(\cos\left(\mathrm{arccos}\left(\dfrac{1}{\sqrt{5}}\right)\right) \cdot \cos (3x) + \sin\left(\mathrm{arccos}\left(\dfrac{1}{\sqrt{5}}\right)\right) \cdot \sin (3x) \right) = \\ = \sqrt{5}\cos\left(3x - \mathrm{arccos}\left(\dfrac{1}{\sqrt{5}}\right)\right)\).

Наибольшее значение \(\sqrt{5}\cos\left(3x - \mathrm{arccos}\left(\dfrac{1}{\sqrt{5}}\right)\right)\) равно \(\sqrt{5}\), значит наибольшее значение \(y\) равно \(3e^{\sqrt{5} - \sqrt{5}} = 3\).

\[y' = \sqrt{3}(2\cos(2x) + 2\sin x) = \sqrt{3}(2 - 4\sin^2x + 2\sin x) = -4\sqrt{3}(\sin x - 1)(\sin x + 0,5).\]

Найдём критические точки: \[-4\sqrt{3}(\sin x - 1)(\sin x + 0,5) = 0\] – при \(\sin x = 1\) и при \(\sin x = -0,5\).

Наибольшее значение функция достигает в тех точках, где либо \(\sin x = -0,5\), либо \(\sin x = 1\).

\(y = 2\sqrt{3}\cos x (\sin x - 1)\).

При \(\sin x = 1\) имеем: \(\cos x = 0\), значит в этих точках \(y = 0\).

При \(\sin x = -0,5\) имеем: \(\cos x = \pm 0,5\sqrt{3}\) и \(y = 2\sqrt{3} (\pm 0,5)\sqrt{3} (-0,5 - 1) = \mp 4,5\).

Итого: наибольшее значение функции \(y\) равно \(4,5\).

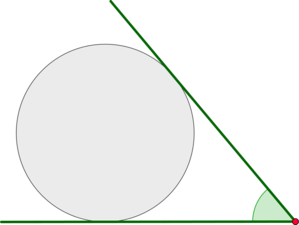
Изобразим график уравнения на координатной плоскости. Оно равносильно \[\left[ \begin{gathered} \begin{aligned} &y=x^2+3x-10\\ &y=-x^2-3x+10 \end{aligned} \end{gathered} \right.\] при \(x\in [-5;2]\). Графиками обоих уравнений являются параболы, пересекающие ось абсцисс в точках \((-5;0)\) и \((2;0)\).
Таким образом, необходимо из точки \(A\) провести две касательные к графику и найти тангенс угла между этими касательными, во внутренней области которого находится график.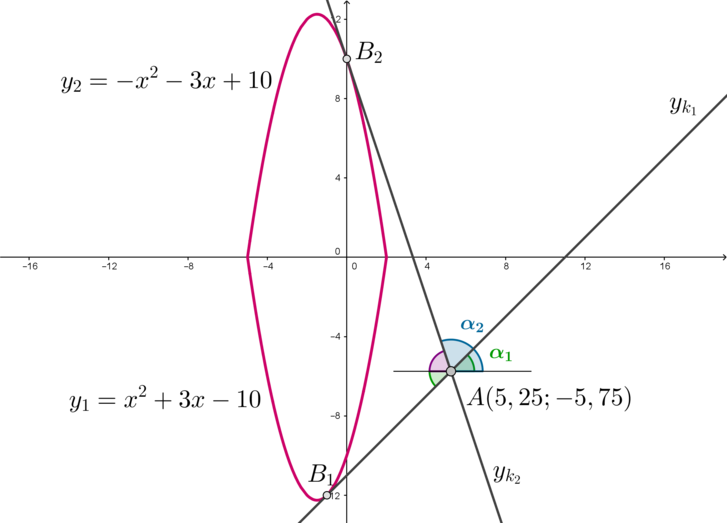

Пусть \(y_{k_1}\) – касательная к \(y_1\) в точке \(B_1\), а \(y_{k_2}\) – касательная к \(y_2\) в точке \(B_2\). Тогда если через точку \(A\) провести прямую параллельно оси абсцисс, то \(\alpha_1\) – угол наклона касательной \(y_{k_1}\), а \(\alpha_2\) – угол наклона касательной \(y_{k_2}\) к положительному направлению оси абсцисс. Тогда угол между касательными, во внутренней области которого находится график, будет равен \[\alpha_1+(180^\circ-\alpha_2)\] Найдем уравнения касательных.
1) \(y_{k_1}\).
\(y'_1=2x+3\), следовательно, если \(x_1\) – точка касания, то \[y_{k_1}=x_1^2+3x_1-10+(2x_1+3)(x-x_1)\] Так как касательная проходит через точку \(A(5,25;-5,75)\), то получаем уравнение: \[-5,75=x_1^2+3x_1-10+(2x_1+3)(5,25-x_1) \quad\Rightarrow\quad 2x_1^2-21x_1-23=0 \quad\Rightarrow\quad \left[\begin{gathered} \begin{aligned} &x_1=-1\\ &x_1=11,5 \end{aligned} \end{gathered}\right.\] Так как график \(y_1\) определен только при \(x\in [-5;2]\), то подходит \(x_1=-1\). Следовательно, уравнение касательной имеет вид: \[y_{k_1}=x-11\] 2) \(y_{k_2}\). Аналогично находим, что \[y_{k_2}=-3x+10.\]
Таким образом, это значит, что \[\begin{aligned} & \mathrm{tg}\,\alpha_1=1\\ &\mathrm{tg}\,\alpha_2=-3 \ \Rightarrow \ \mathrm{tg}\,(180^\circ-\alpha_2)=3\end{aligned}\] Следовательно, \[\mathrm{tg}\,(\alpha_1+(180^\circ-\alpha_2))=\dfrac{\mathrm{tg}\,\alpha_1 +\mathrm{tg}\,(180^\circ-\alpha_2)}{1-\mathrm{tg}\,\alpha_1\cdot \mathrm{tg}\,(180^\circ-\alpha_2)}=\dfrac{1+3}{1-1\cdot 3}=-2.\]