Параллелограмм: свойство его биссектрисы (страница 3)
Готовиться с нами - ЛЕГКО!

Биссектриса параллелограмма — это отрезок, соединяющий вершину параллелограмма с точкой на одной из двух противоположных сторон и делящий угол при вершине пополам.
\(\bullet\) Биссектриса параллелограмма отсекает от него равнобедренный треугольник.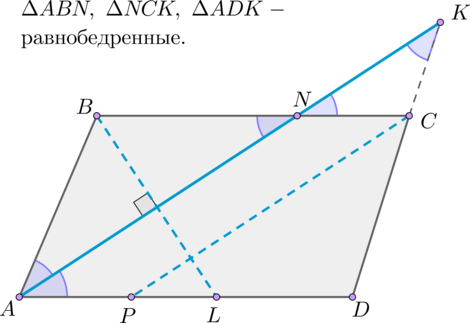
\(\bullet\) Биссектрисы соседних углов параллелограмма взаимно перпендикулярны: \(BL\perp AN\).
\(\bullet\) Биссектрисы противоположных углов параллелограмма параллельны: \(AN\parallel CP\).
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна \(5\). Найдите его большую сторону.
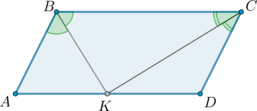
\(AB=5\). Так как в параллелограмме противоположные стороны параллельны, то \(\angle AKB=\angle KBC\) как накрест лежащие при \(AD\parallel BC\) и секущей \(BK\). Следовательно, \(\angle AKB=\angle
ABK\), то есть \(\triangle ABK\) равнобедренный: \(AK=AB\).
Аналогично \(DC=DK\).
Так как в параллелограмме противоположные стороны равны, то \(AK=AB=5=CD=DK\). Следовательно, \(AD=5+5=10\) – большая сторона.

