Задачи на нахождение площади и периметра треугольника (страница 2)
Готовиться с нами - ЛЕГКО!

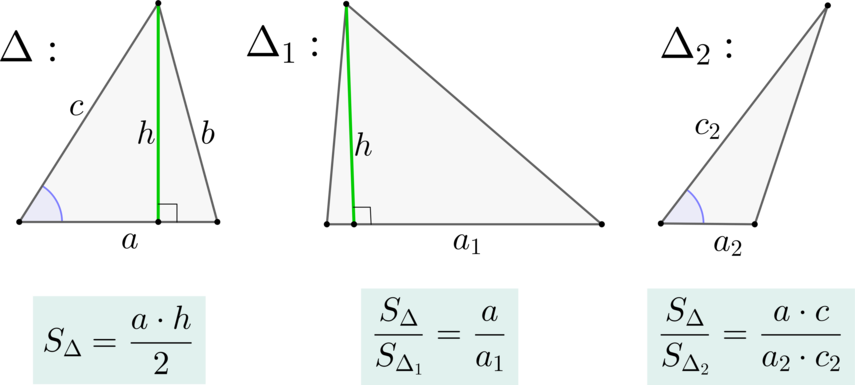
\(\blacktriangleright\) Площадь треугольника равна полупроизведению основания \(a\) и высоты \(h\), проведенной к этому основанию.
\(\blacktriangleright\) Формула Герона для площади треугольника:
\(\large{S_{\triangle}=\sqrt{p(p-a)(p-b)(p-c)}}\), где \(p\) – полупериметр.
\(\blacktriangleright\) Если треугольники имеют равные высоты (\(\triangle\) и \(\triangle_{1}\)), то их площади относятся как основания, к которым эти высоты проведены.
Как следствие: медиана треугольника делит его на два равновеликих (равных по площади) треугольника.
\(\blacktriangleright\) Если треугольники имеют по равному углу (\(\triangle\) и \(\triangle_{2}\)), то их площади относятся как произведения сторон, образующих этот угол.
У треугольника со сторонами \(9\) и \(6\) проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна \(4\). Чему равна высота, проведенная ко второй стороне?
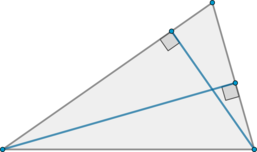
Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне. Следовательно, с одной стороны, \(S=0,5\cdot 9\cdot 4\), а с другой стороны \(S=0,5\cdot 6\cdot h\), где \(h\) – высота, которую нужно найти. Следовательно, \[0,5\cdot 9\cdot 4=0,5\cdot 6\cdot h\quad\Leftrightarrow\quad h=6\]
Боковая сторона равнобедренного треугольника равна \(5\), а основание равно \(6\). Найдите площадь этого треугольника.
Проведем высоту к основанию. В равнобедренном треугольнике высота, проведенная к основанию, является и медианой.
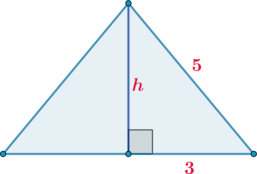
Таким образом мы получили прямоугольный треугольник с катетами \(h\) и \(3\) и гипотенузой \(5\). По теореме Пифагора найдем \(h=\sqrt{5^2-3^2}=4\) (заметим, что такой треугольник называется “египетским”).
Так как площадь треугольника равна половине произведения высоты на основание, к которому она проведена, то \[S=\dfrac12 h\cdot 6=12\]
Проекция диагонали равнобедренной трапеции на ее большее основание равна \(6\), боковая сторона равна \(3\). Найдите площадь трапеции, если угол при её меньшем основании равен \(150^\circ\).
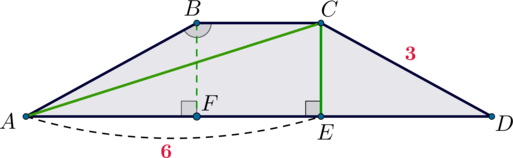
\(AE\) - есть проекция диагонали \(AC\) на основание трапеции \(AD\). Запишем формулу площади трапеции:
\[S=CE\cdot\dfrac{BC+AD}2.\]
Проведя вторую высоту \(BF\), заметим, что треугольники \(AFB\) и \(DEC\) равны по двум углам и стороне между ними, т. к. боковые стороны в равнобедренной трапеции равны, отсюда следует, что:
\[AF=ED \Rightarrow FE=AD-2ED=BC.\]
Подставим полученные данные в формулу площади трапеции:
\[CE \cdot \dfrac{BC+AD}{2}= CE \cdot \dfrac{AD-2ED+AD}{2}= CE \cdot \dfrac{2 \cdot(AE+ED) - 2ED}{2}= CE \cdot AE.\]
Чтобы найти высоту \(CE\), заметим, что \(\angle ABC= 150^\circ\Rightarrow \angle ABF = 150^\circ-90^\circ = 60^\circ\Rightarrow BF=CE=\cos(60^\circ)\cdot AB\).
Теперь подставим высоту в формулу и найдем площадь трапеции:
\[S=AE\cdot\cos{60^\circ}\cdot AB= 6\cdot\dfrac{1}{2}\cdot 3=9.\]
В треугольнике \(ABC\): \(CD\) – высота, \(CD = \sqrt{12}\), \(AB = \pi\sqrt{3}\), \(AC = 2\pi\). Найдите расстояние от точки \(B\) до прямой, содержащей отрезок \(AC\).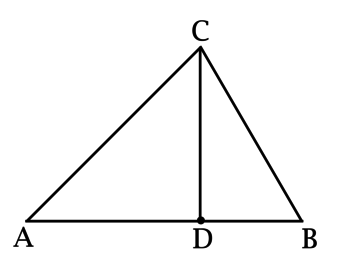
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на эту прямую. Обозначим её за \(h\).
Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию. Так как площадь треугольника не зависит от выбора основания, то \(0,5 \cdot AB \cdot CD = 0,5 \cdot AC \cdot h\), откуда \(0,5\cdot \pi\sqrt{3}\cdot\sqrt{12} = 0,5 \cdot 2\pi \cdot h\), значит, \(h = 3\).
В треугольнике \(ABC\): \(BD = 2\) – высота, \(BC = 4\), \(AC = 12\). Найдите расстояние от точки \(A\) до прямой, содержащей отрезок \(BC\).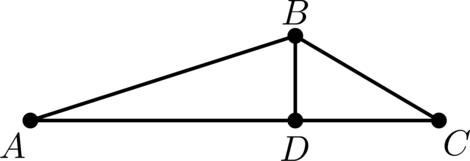
Расстояние от точки до прямой равно длине перпендикуляра, опущенного из этой точки на прямую, следовательно, расстояние от точки \(A\) до прямой, содержащей отрезок \(BC\), равно длине высоты \(AE\).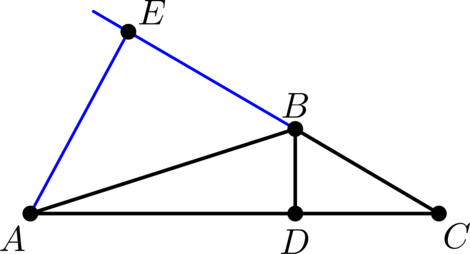
Посчитаем площадь треугольника \(ABC\) двумя способами: \[0,5AC\cdot BD = S_{ABC} = 0,5AE\cdot BC\,,\] откуда \(12 = 2AE\), следовательно, \(AE = 6\).
В треугольнике \(ABC\): точки \(D\) и \(E\) лежат на \(AB\), причём \(\dfrac{AD + BE}{AB} = \dfrac{2}{3}\). Площадь треугольника \(ACD\) равна \(10\), \(\dfrac{S_{CEB}}{S_{CED}} = \dfrac{6}{5}\). Найдите площадь треугольника \(ABC\).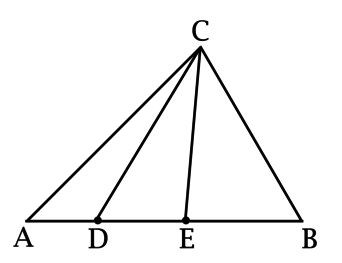
Пусть \(h\) – длина высоты, опущенной из точки \(C\) на \(AB\), тогда \(S_{ABC} = 0,5\cdot AB\cdot h\).
\(S_{CEB} = 0,5\cdot EB\cdot h\), \(S_{CED} = 0,5\cdot DE\cdot h\), откуда \(\dfrac{6}{5} = \dfrac{S_{CEB}}{S_{CED}} = \dfrac{0,5\cdot EB\cdot h}{0,5\cdot DE\cdot h} = \dfrac{EB}{DE}\), но \(DE = AB - (AD + BE) = AB - \dfrac{2}{3}\cdot AB = \dfrac{1}{3}\cdot AB\), откуда \(EB = \dfrac{6}{5}\cdot \dfrac{1}{3}\cdot AB = \dfrac{2}{5}\cdot AB\), тогда \(AD = AB - (DE + EB) = AB - \dfrac{1}{3}\cdot AB - \dfrac{2}{5}\cdot AB = \dfrac{4}{15}\cdot AB\).
\(10 = S_{ACD} = 0,5\cdot AD\cdot h = 0,5\cdot \dfrac{4}{15}\cdot
AB\cdot h = \dfrac{4}{15}\cdot S_{ABC}\), откуда \(S_{ABC} =
10\cdot\dfrac{15}{4} = 37,5\).
Найдите квадрат площади треугольника \(ABC\), если \(AC =3\), \(BC= 4\), а медианы, проведенные из вершин \(A\) и \(B\), взаимно перпендикулярны.
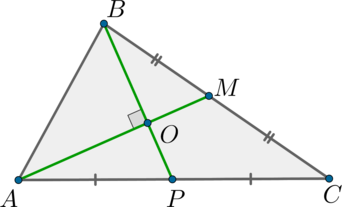
Т.к. \(BP\)- медиана, то \(S_{ABP} = S_{PBC}\Rightarrow S_{ABC} = 2\cdot S_{ABP}\).
Т.к. \(AM\) и \(BP\) - медианы, то точка \(O\) делит их в отношении 2:1, считая от вершины, тогда если \(OM = x\Rightarrow AO = 2x, OP = y\Rightarrow BO=2y\). Получим систему уравнений:
\[\begin{cases} x^2 + 4y^2 = 4\\ 4x^2 + y^2 = 2,25 \end{cases}\]
Из системы находим \(x\) и \(y\):
\[x = \sqrt{\dfrac{1}3}, y =\sqrt{\dfrac{2,75}3}\]
Тогда: \(S_{ABP} = 0,5\cdot 2x\cdot 3y = 3\cdot \sqrt{\dfrac{1}3}\cdot \sqrt{\dfrac{2,75}3}\).
\[S_{ABC} = 2\cdot 3\cdot \sqrt{\dfrac{1}3}\cdot \sqrt{\dfrac{2,75}3} = \sqrt{11}.\] \[(S_{ABC})^2 = 11.\]



