Задачи на прямолинейное движение (страница 4)
Готовиться с нами - ЛЕГКО!

Если тело движется с постоянной скоростью, то пройденное им расстояние удовлетворяет следующей формуле: \[{\large{S=v\cdot t}}\] где \(v\) — его скорость, \(t\) — время, в течение которого оно двигалось.
Другие вариации данной формулы: \(v=\dfrac St\) и \(t=\dfrac Sv\)
Некоторые частные случаи:
\(\blacktriangleright\) Когда два тела движутся навстречу друг другу со скоростями \(v_1\) и \(v_2\) соответственно, то \(v_1+v_2\) — их скорость сближения. Если \(S\) — расстояние между ними на момент начала движения, \(t\) — время, через которое они встретились, то:
\(\blacktriangleright\) Когда тела движутся в противоположном направлении (например, из одной точки), то \(v_1+v_2\) — их скорость удаления. Тогда расстояние \(S\) между ними через время \(t\):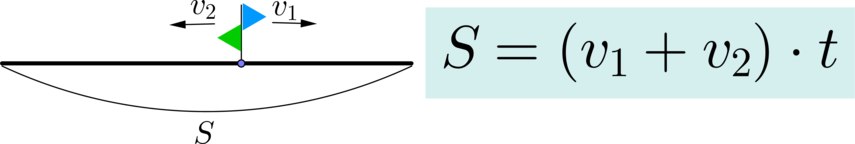
\(\blacktriangleright\) Когда тела движутся друг за другом, то:
\((1) \quad v_1>v_2\). Тогда первое тело догонит второе через некоторой время \(t\).
\(v_1-v_2\) — скорость сближения. Если \(S\) — расстояние между ними в начале движения, то: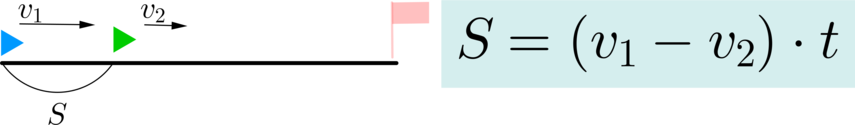
\((2) \quad v_1<v_2\). Тогда первое тело никогда не догонит второе и расстояние между ними будет только увеличиваться.
\(v_2-v_1\) — скорость удаления. Если \(S\) — расстояние между ними на момент начала движения, то через время \(t\) расстояние между ними будет:
\((3) \quad v_1=v_2\). Тогда первое тело никогда не догонит второе, но расстояние между ними всегда будет оставаться одинаковым.
Поезд длиной 1 км проходит мимо километрового столба за 1 мин, а через туннель при той же скорости – за 3 мин. Какова длина туннеля? Ответ дайте в километрах.

Из картинки видно, что “поезд проходит мимо столба” – это то же самое, что “поезд проходит расстояние, равное длине поезда”, а “поезд проходит через туннель” – это то же самое, что “поезд проходит расстояние, равное длине поезда плюс длине туннеля”.
Следовательно, так как длина поезда 1 км, а мимо столба он проходит за 1 мин, то его скорость равна 1 км/мин. Следовательно, 1 км/мин \(\cdot\) 3 мин \(=\) 3 км – длина поезда плюс длина туннеля. Следовательно, длина туннеля равна 2 км.
Пристани А и В расположены на берегу моря на расстоянии 704 км друг от друга. Паром отправился из А в В с постоянной скоростью. Прибыв в В, он отправился обратно со скоростью, на 5 км/ч больше прежней, при этом сделав по пути остановку на 20 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость парома на пути из В в А. Ответ дайте в км/ч.
Пусть \(x\) км/ч – скорость парома из А в В. Тогда можно составить такую картинку-схему: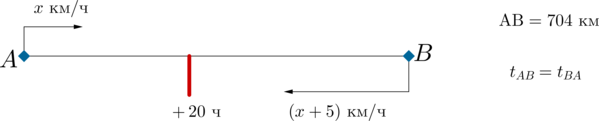
Время в часах, которое паром затратил из А в В, равно \[\dfrac{704}{x}\] Время в часах, которое он затратил из В в А, равно \[\dfrac{704}{x+5}+20\] Так как это время оказалось одинаковым, то получается следующее уравнение \[\dfrac{704}x=\dfrac{704}{x+5}+20 \quad\Leftrightarrow\quad
\dfrac{704(x+5)-704x}{x(x+5)}=20 \quad\Leftrightarrow\quad
\dfrac{176}{x(x+5)}=1 \quad\Leftrightarrow\quad x^2+5x-176=0\] Дискриминант \(D=5^2+4\cdot 176=729=27^2\), следовательно, корни \[x_1=\dfrac{-5+27}{2}=11 \quad {\small{\text{и}}}
\quad x_2=\dfrac{-5-27}{2}=-16\] Так как скорость – величина положительная, то \(x=11\).
Не забудем вернуться к условию и проверить, что необходимо было найти: скорость парома на пути из В в А. Следовательно, ответ \(x+5=16\).
Два поезда движутся навстречу друг другу – один со скоростью 70 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметим, что первый поезд прошел мимо него за 12 секунд. Какова длина первого поезда? Ответ дайте в метрах.
Заметим, что фраза “первый поезд прошел мимо пассажира за 12 с” означает, что с того момента, как пассажир увидел голову поезда, до того момента, как он увидел хвост поезда, прошло 12 с. Следовательно, неважно, где именно в поезде в этот момент находился пассажир. Поэтому пусть пассажир находился прямо в начале поезда.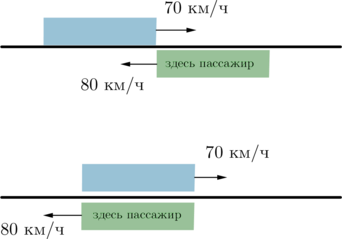
Первая картинка – когда пассажир увидел голову поезда, вторая – хвост поезда.
Заметим, что за каждую секунду первый поезд проезжает \(\dfrac{70000}{3600}=\dfrac{175}9\) м, второй – \(\dfrac{80000}{3600}=\dfrac{200}9\) м.
Следовательно, за каждую секунду пассажир удаляется от головы первого поезда на \(\dfrac{175}9+\dfrac{200}9=\dfrac{125}3\) м. Следовательно, через 12 с он удалится от головы поезда на \(\dfrac{125}3\cdot 12=500\) м. Так как в этот момент он будет видеть хвост поезда, то это значит, что 500 м и есть длина первого поезда.
Два автомобиля выехали с постоянными скоростями из пунктов \(A\) и \(B\) навстречу друг другу. Известно, что скорость одного из них в \(1,2\) раза больше, чем скорость другого. Они встретелись через \(t\) часов. Известно, что медленному автомобилю понадобилось \(T\) часов, чтобы добраться до противоположного пункта. Найдите \(\dfrac{T}{t}\).
Пусть \(v\, км/ч\) – скорость медленного автомобиля, тогда \(1,2v\, км/ч\) – скорость быстрого автомобиля, следовательно, скорость сближения автомобилей равна \(v + 1,2v = 2,2v\, км/ч\).
Пусть \(S\, км\) – расстояние между пунктами \(A\) и \(B\), тогда \(t = \dfrac{S}{2,2v}\), а \(T = \dfrac{S}{v}\), следовательно, \[\dfrac{T}{t} = \dfrac{S}{v} : \dfrac{S}{2,2v} = 2,2\,.\]
Отчалив одновременно от противоположных берегов реки, два парома встречаются на расстоянии \(900\) метров от левого берега. Прибыв к месту назначения, каждый паром тут же отправляется обратно. Во второй раз паромы вновь встречаются на расстоянии \(300\) метров от правого берега. Паромы двигаются с постоянной скоростью. Чему равна ширина реки? Ответ дайте в километрах.
Рассмотрим схематичный рисунок: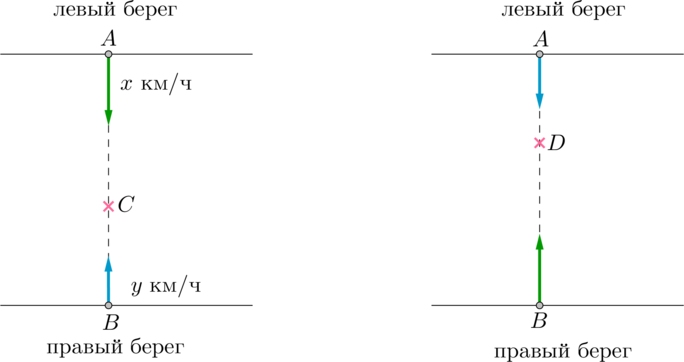
Условно назовем паром, отчаливший от левого берега, зеленым, а паром, отчаливший от правого – синим. Пусть скорость зеленого \(x\) км/ч, синего \(y\) км/ч.
Из условия задачи следует, что \(AC=0,9\) км, \(BD=0,3\) км.
Пусть \(BC=S\). Тогда \(AB=AC+BC=0,9+S\). Так как до первой встречи паромы двигались одинаковое количество времени, то можно составить равенство: \[\dfrac Sy=\dfrac {0,9}x \quad\Rightarrow\quad \dfrac xy=\dfrac{0,9}S\]
После первой встречи и до второй встречи синий прошел расстояние, равное \(AC+AD=AC+(AB-BD)=0,9+0,9+S-0,3=1,5+S\), а зеленый – равное \(BC+BD=S+0,3\). Время, потраченное на путь у каждого парома, также было одинаковым. Следовательно, можно составить второе равенство: \[\dfrac{1,5+S}y=\dfrac{S+0,3}x \quad\Rightarrow\quad \dfrac xy=\dfrac{S+0,3}{1,5+S}\]
Таким образом, из полученных двух равенств можно заключить: \[\dfrac{0,9}S=\dfrac{S+0,3}{1,5+S} \quad\Rightarrow\quad S^2-0,6S-0,9\cdot 1,5=0\]
По теореме Виета корнями уравнения будут числа \(-0,9\) и \(1,5\). Так как \(S\) – длина отрезка, то есть неотрицательная величина, то \(S=1,5\). Следовательно, ширина реки равна \(AB=1,5+0,9=2,4\).
Из пункта А в пункт Б одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй первую половину пути проехал со скоростью \(84\) км/ч, а вторую половину пути со скоростью, на \(11,2\) км/ч меньшей скорости первого, в результате чего оба автомобилиста прибыли в пункт Б одновременно. Найдите скорость первого автомобилиста, если известно, что она была больше 50 км/ч. Ответ дайте в км/ч.
Пусть скорость первого автомобилиста равна \(x\) км/ч, \(S\) км – расстояние от А до Б. Тогда можно составить такую картинку-схему: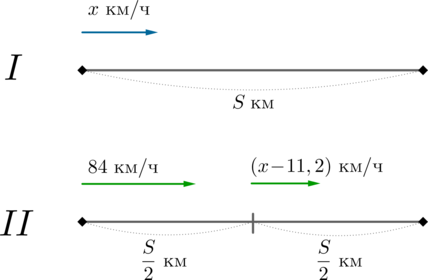
Тогда время в часах, которое первый затратил на дорогу, равно \[\dfrac Sx\] Время в часах, которое второй затратил на дорогу, равно \[\dfrac{\frac S2}{84}+\dfrac{\frac S2}{x-11,2}\] Так как оба прибыли одновременно в пункт Б, то есть затратили на дорогу одинаковое время, то получаем следующее уравнение: \[\dfrac Sx=\dfrac{\frac S2}{84}+\dfrac{\frac S2}{x-11,2}\] Заметим, что можно разделить обе части уравнения на \(S\), так как \(S\ne 0\). Приведем к общему знаменателю и перенесем все слагаемые в одну сторону: \[\dfrac{x^2-(84+11,2)x+2\cdot 84\cdot 11,2}{2\cdot 84\cdot x\cdot (x-11,2)}=0\] Решим уравнение \(x^2-(84+11,2)x+2\cdot 84\cdot 11,2=0\). Домножим его на \(10\): \(10x^2-952x+2\cdot 84\cdot 112=0\).
Дискриминант \[D=952^2-4\cdot 10\cdot 2\cdot 84\cdot 112=7^2\cdot 2^6\cdot
17^2-2^{10}\cdot 3\cdot 5\cdot 7^2=7^2\cdot 2^6\cdot
(289-240)=(7\cdot 2^3\cdot 7)^2=392^2\] Следовательно, корнями будут \[x_1=\dfrac{952+392}{20}=67,2 \quad {\small{\text{и}}}
\quad x_2=\dfrac{952-392}{20}=28\] Так как скорость больше 50, то ответом будет число 67,2.
Из пункта А в пункт С выехал мотоциклист, скорость которого 16 км/ч. Одновременно с ним из пункта В, находящегося между пунктами А и С, в пункт С выехал второй мотоциклист, скорость которого 31 км/ч. Через сколько минут расстояние между мотоциклистами будет 17,5 км? Расстояние между пунктами A и B равно 10 км.
Если задача допускает несколько вариантов ответа, в бланк укажите их сумму.
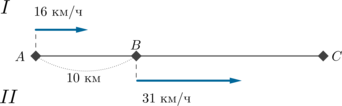
Заметим, что так как более быстрый мотоциклист находится впереди, то расстояние между мотоциклистами будет только увеличиваться (то есть они будут только отдаляться друг от друга). Значит, в задаче будет только один ответ.
Следовательно, расстояние между ними должно измениться на \(17,5-10=7,5\) км (так как изначально они находились на расстоянии 10 км друг от друга). Скорость удаления мотоциклистов равна \(31-16=15\) км/ч. Следовательно, время, через которое расстояние между ними увеличится еще на 7,5 км, равно \(7,5:15=0,5\) часа или \(30\) минут.



