Задачи с окружностями (страница 4)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Радикальная ось перпендикулярна линии центров окружностей. Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.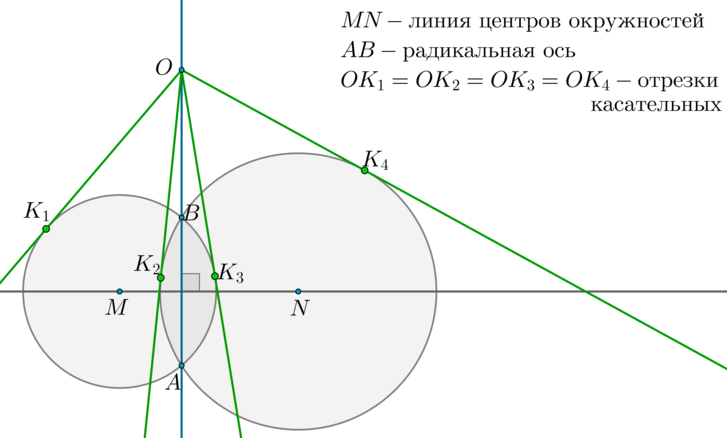
\(\blacktriangleright\) Пусть две окружности с центрами \(M\) и \(N\) касаются внешним образом в точке \(A\). Две общие касательные (внутренняя и внешняя) \(a\) и \(b\) этих окружностей пересекаются в точке \(B\). Точки касания — точки \(A, K_1, K_2\). Тогда \[{\large{K_1B=AB=K_2B}}\] \[{\large{\angle K_1AK_2=90^\circ}}\]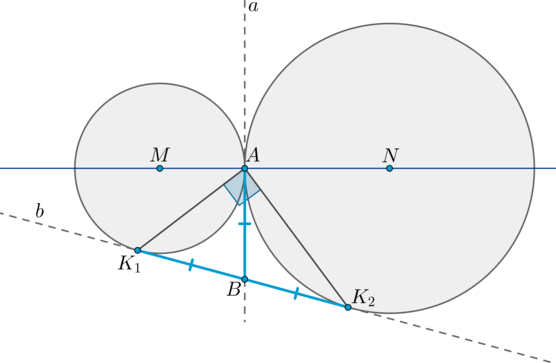
\(\blacktriangleright\) Пусть две окружности касаются внешним образом в точке \(A\). Через точку \(A\) проведены две прямые \(B_1B_2\) и \(C_1C_2\), пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: \[{\large{\triangle AB_1C_1 \sim \triangle
AB_2C_2}}\] \[{\large{B_1C_1\parallel B_2C_2}}\]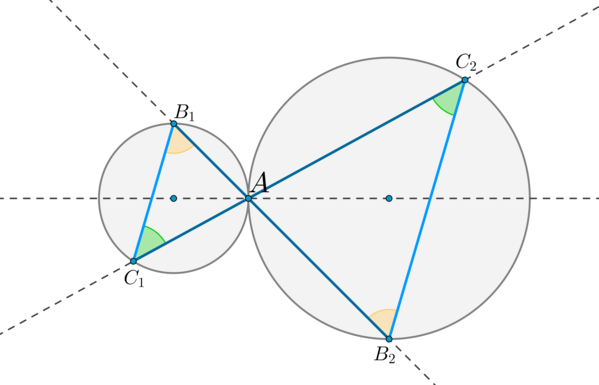
\(\blacktriangleright\) Формула Эйлера: Пусть \(R\) — радиус описанной около треугольника окружности, \(r\) — радиус вписанной окружности. Тогда расстояние между центрами этих окружностей вычисляется по формуле: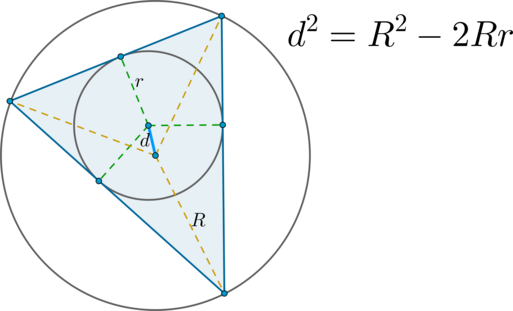
\(\blacktriangleright\) Теорема о бабочке: Пусть через середину хорды \(AB\) — точку \(O\), проведены две хорды \(MN\) и \(KP\). Пусть \(MP\cap AB=X, KN\cap AB=Y\). Тогда \[{\large{OX=OY}}\]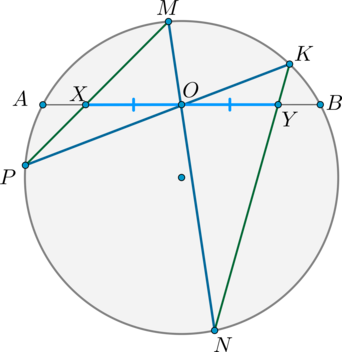
\(ABCDEF\) – выпуклый шестиугольник, про который известно, что \(\angle A > 120^\circ\), \(\angle B\leqslant 70^\circ\), \(\angle C \geqslant 130^\circ\), \(\angle E \geqslant 110^\circ\).
а) Докажите, что около хотя бы одного из четырёхугольников \(ABCD\), \(ACDE\) и \(ACDF\) нельзя описать окружность.
б) Найдите периметр \(ABCDEF\), если \(AB + CD + EF = 11\) и в \(ABCDEF\) можно вписать окружность.
а) Если около четырёхугольника \(ABCD\) можно описать окружность, то она будет описанной и для треугольника \(ACD\).
Если около четырёхугольника \(ACDE\) можно описать окружность, то она будет описанной и для треугольника \(ACD\).
Если около четырёхугольника \(ACDF\) можно описать окружность, то она будет описанной и для треугольника \(ACD\).
Так как около треугольника можно описать ровно одну окружность, то описанные около четырёхугольников \(ABCD\), \(ACDE\) и \(ACDF\) окружности должны совпасть, следовательно, тогда шестиугольник \(ABCDEF\) также будет вписанным.
Таким образом, достаточно показать, что около \(ABCDEF\) нельзя описать окружность.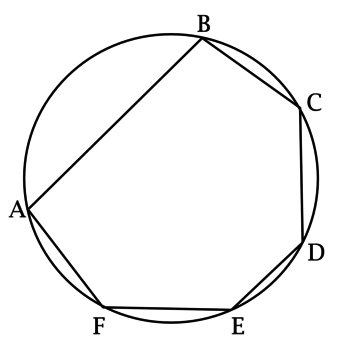
Пусть шестиугольник \(ABCDEF\) – вписанный, тогда
\[\begin{aligned} &\angle A + \angle C + \angle E = 0,5\cdot\smile BCDEF + 0,5\cdot\smile BAFED + 0,5\cdot\smile FABCD =\\ &= 0,5(360^\circ - \smile BAF) + 0,5(360^\circ - \smile BCD) + 0,5(360^\circ - \smile FED) =\\ &= 540^\circ - 0,5(\smile BAF + \smile BCD + \smile FED) = 360^\circ, \end{aligned}\]
но \(\angle A + \angle C + \angle E > 360^\circ\), следовательно, около \(ABCDEF\) нельзя описать окружность, откуда следует, что около хотя бы одного из четырёхугольников \(ABCD\), \(ACDE\) и \(ACDF\) нельзя описать окружность.
б)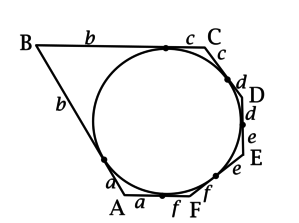
Пользуясь тем, что отрезки касательных к окружности, проведённых из одной точки, равны, обозначим длины отрезков касательных, проведённых из точки \(A\), через \(a\), длины отрезков касательных, проведённых из точки \(B\), через \(b\) и т.д.
\[11 = AB + CD + EF = a + b + c + d + e + f = 0,5\cdot P_{ABCDEF},\] откуда \(P_{ABCDEF} = 22\).
б) \(22\).
\(ABCDE\) – выпуклый пятиугольник, про который известно, что \(\angle A\geq 120^\circ\), \(\angle B\leq 70^\circ\), \(\angle C\geq 130^\circ\).
а) Докажите, что около хотя бы одного из четырёхугольников \(ABCD\) и \(ACDE\) нельзя описать окружность.
б) Найдите \(AE\), если в \(ABCDE\) вписана окружность, касающаяся стороны \(AE\) в её середине, \(P_{ABCDE} = 10\), \(AB + CD + AE = 6,5\).
а) Если около четырёхугольника \(ABCD\) можно описать окружность, то она будет описанной и для треугольника \(ACD\).
Если около четырёхугольника \(ACDE\) можно описать окружность, то она будет описанной и для треугольника \(ACD\).
Так как около треугольника можно описать ровно одну окружность, то описанные около четырёхугольников \(ABCD\) и \(ACDE\) окружности должны совпасть, следовательно, тогда пятиугольник \(ABCDE\) также будет вписанным.
Таким образом, достаточно показать, что около \(ABCDE\) нельзя описать окружность.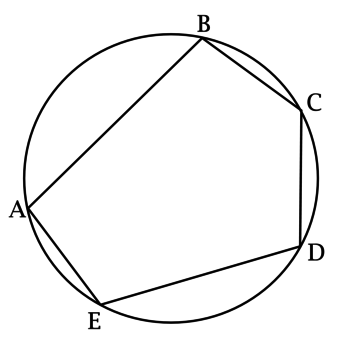
Пусть пятиугольник \(ABCDE\) – вписанный, тогда \[\angle A + \angle C = 0,5\cdot\smile BCDE + 0,5\cdot\smile BAED = 0,5\cdot 180^\circ + \smile DE,\] где \(\smile DE\) отлична от \(\smile DCBAE\). Таким образом, \(\angle A + \angle C > 180^\circ\).
Аналогично для любых двух несмежных углов вписанного пятиугольника: их сумма больше 180 градусов.
По условию \(\angle A + \angle C \geq 250^\circ\), тогда \(\angle B + \angle D + \angle E\leq 290^\circ\), но \(\angle B\leq 70^\circ\), тогда \[2\angle B + \angle D + \angle E\leq 360^\circ.\]
Если бы около \(ABCDE\) можно было описать окружность, то было бы верно \(\angle B + \angle E > 180^\circ\) и \(\angle B + \angle D > 180^\circ\), тогда было бы \[\angle E + 2\angle B + \angle D > 360^\circ,\] что не верно для \(ABCDE\), следовательно, около \(ABCDE\) нельзя описать окружность, откуда следует, что около хотя бы одного из четырёхугольников \(ABCD\) и \(ACDE\) нельзя описать окружность.
б) 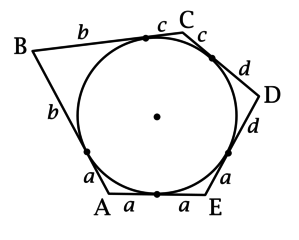
Пользуясь тем, что отрезки касательных к окружности, проведённых из одной точки, равны, а окружность касается \(AE\) в середине, обозначим длины отрезков касательных, проведённых из точки \(A\), через \(a\), длины отрезков касательных, проведённых из точки \(B\), через \(b\) и т.д. \[P_{ABCDE} = 4a + 2b + 2c + 2d = 10,\] тогда \(2a + b + c + d = 5\).
\[AB + CD + AE = 3a + b + c + d = a + (2a + b + c + d) = a + 5 = 6,5,\] откуда \(a = 1,5\), следовательно, \(AE = 3\).
б) \(3\).

