Монотонность функций
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Функция \(f(x)\) называется возрастающей на промежутке \(X\), если для любых \(x_1, x_2\in
X\), таких что \(x_1<x_2\), выполнено \(f(x_1)<f(x_2)\).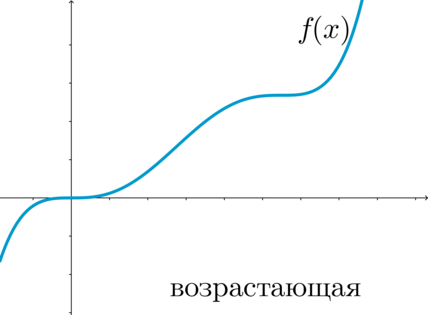
Функция называется неубывающей на промежутке \(X\), если для любых \(x_1, x_2\in X\), таких что \(x_1<x_2\), выполнено \(f(x_1)\leq f(x_2)\).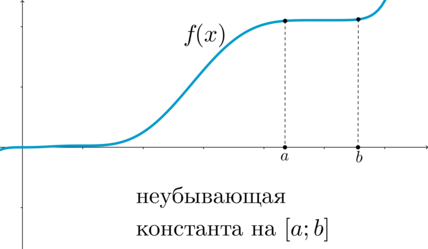
\(\blacktriangleright\) Функция \(f(x)\) называется убывающей на промежутке \(X\), если для любых \(x_1, x_2\in X\), таких что \(x_1<x_2\), выполнено \(f(x_1)>f(x_2)\).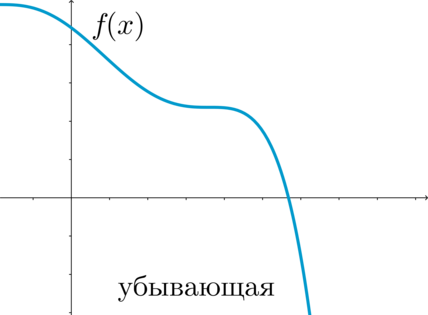
Функция называется невозрастающей на промежутке \(X\), если для любых \(x_1, x_2\in X\), таких что \(x_1<x_2\), выполнено \(f(x_1)\geq f(x_2)\).
\(\blacktriangleright\) Возрастающие и убывающие функции называют строго монотонными, а невозрастающие и неубывающие — просто монотонными.
\(\blacktriangleright\) Основные свойства:
I. Если функция \(f(x)\) — строго монотонна на \(X\), то из равенства \(x_1=x_2\) (\(x_1,x_2\in X\)) следует \(f(x_1)=f(x_2)\), и наоборот.
Пример: функция \(f(x)=\sqrt x\) является строго возрастающей при всех \(x\in [0;+\infty)\), поэтому из равенства \(\sqrt x=\sqrt 4\) следует \(x=4\).
II. Если функция \(f(x)\) — строго монотонна на \(X\), то уравнение \(f(x)=c\), где \(c\) — некоторое число, всегда имеет не более одного решения на \(X\).
Пример: функция \(f(x)=x^2\) является строго убывающей при всех \(x\in
(-\infty;0]\), поэтому уравнение \(x^2=9\) имеет на этом промежутке не более одного решения, а точнее одно: \(x=-3\).
функция \(f(x)=-\dfrac 1{x+1}\) является строго возрастающей при всех \(x\in (-1;+\infty)\), поэтому уравнение \(-\dfrac 1{x+1}=0\) имеет на этом промежутке не более одного решения, а точнее ни одного, т.к. числитель левой части никогда не может быть равен нулю.
III. Если функция \(f(x)\) — неубывает (невозрастает) и непрерывна на отрезке \([a;b]\), причем на концах отрезка она принимает значения \(f(a)=A, f(b)=B\), то при \(C\in [A;B]\) (\(C\in
[B;A]\)) уравнение \(f(x)=C\) всегда имеет хотя бы одно решение.
Пример: функция \(f(x)=x^3\) является строго возрастающей (то есть строго монотонной) и непрерывной при всех \(x\in\mathbb{R}\), поэтому при любом \(C\in (-\infty;+\infty)\) уравнение \(x^3=C\) имеет ровно одно решение: \(x=\sqrt[3]{C}\).
Найдите все значения параметра \(a\), при каждом из которых уравнение \[27x^6+(a-x)^3+3x^2=x-a\]
имеет ровно два корня.
Перепишем уравнение в виде: \[(3x^2)^3+3x^2=(x-a)^3+(x-a)\] Рассмотрим функцию \(f(t)=t^3+t\). Тогда уравнение перепишется в виде: \[f(3x^2)=f(x-a)\] Исследуем функцию \(f(t)\). \[f'(t)=3t^2+1>0\] Следовательно, функция \(f(t)\) возрастает при всех \(t\). Значит, каждому значению функции \(f(t)\) соответствует ровно одно значение аргумента \(t\). Следовательно, для того, чтобы уравнение имело корни, нужно: \[3x^2=x-a \quad\Leftrightarrow\quad 3x^2-x+a=0\] Чтобы полученное уравнение имело два корня, нужно, чтобы его дискриминант был положительным: \[D=1-12a>0 \quad\Rightarrow\quad a<\dfrac1{12}\]
\(\left(-\infty;\dfrac1{12}\right)\)
Найдите все значения параметра \(a\), при которых уравнение \[7^{ax^2-2x}-7^{x^2-1}=\sqrt[7]{2x-ax^2}-\sqrt[7]{1-x^2}\]
имеет два корня.
(Задача от подписчиков.)
Сделаем замену: \(ax^2-2x=t\), \(x^2-1=u\). Тогда уравнение примет вид: \[7^t-7^u=\sqrt[7]{-t}-\sqrt[7]{-u} \quad\Leftrightarrow\quad 7^t+\sqrt[7]t=7^u+\sqrt[7]u\] Рассмотрим функцию \(f(w)=7^w+\sqrt[7]w\). Тогда наше уравнение примет вид: \[f(t)=f(u).\]
Найдем производную \[f'(w)=7^w\ln7+\dfrac1{7\cdot \sqrt[7]{w^6}}.\] Заметим, что при всех \(w\ne 0\) производная \(f'(w)>0\), т.к. \(7^w>0\), \(w^6>0\). Заметим также, что сама функция \(f(w)\) определена при всех \(w\). Т.к. к тому же \(f(w)\) непрерывна, то мы можем сделать вывод, что \(f(w)\) возрастает на всем \(\mathbb{R}\).
Значит, равенство \(f(t)=f(u)\) возможно тогда и только тогда, когда \(t=u\). Вернемся к изначальным переменным и решим полученное уравнение:
\[ax^2-2x=x^2-1\quad\Leftrightarrow\quad (a-1)x^2-2x+1=0\] Для того, чтобы данное уравнение имело два корня, оно должно быть квадратным и его дискриминант должен быть положительным:
\[\begin{cases} a-1\ne 0\\ 4-4(a-1)>0\end{cases} \quad\Leftrightarrow\quad \begin{cases}a\ne1\\a<2\end{cases}\]
\((-\infty;1)\cup(1;2)\)
Найдите все положительные значения параметра \(a\), при которых уравнение
\[5((ax-2)^3-(x^2-2)^3+3e^{ax}-3e^{x^2})=\\ =6e^{x^2}\cdot \ \sin{2x^2} - 6e^{ax}\cdot \ \sin{2ax} + 3e^{x^2}\cdot \ \cos{2x^2} - 3e^{ax}\cdot \ \cos{2ax}\]
имеет как минимум \(2\) решения.
Перенесем все слагаемые, содержащие \(ax\), влево, а содержащие \(x^2\) – вправо, и рассмотрим функцию
\[f(t)=5(t-2)^3+15e^t+6e^t\cdot \sin{2t} +3e^t\cdot \cos{2t}\]
Тогда исходное уравнение примет вид:
\[f(ax)=f(x^2)\]
Найдем производную:
\[f'(t)=15(t-2)^2+15e^t\cdot (1+\cos{2t})\]
Т.к. \((t-2)^2 \geqslant 0, \ e^t>0, \ 1+\cos{2t} \geqslant 0\), то \(f'(t)\geqslant 0\) при любых \(t\in \mathbb{R}\).
Причем \(f'(t)=0\), если \((t-2)^2=0\) и \(1+\cos{2t}=0\) одновременно, что не выполняется ни при каких \(t\). Следовательно, \(f'(t)> 0\) при любых \(t\in \mathbb{R}\).
Таким образом, функция \(f(t)\) строго возрастает при всех \(t\in \mathbb{R}\).
Значит, уравнение \(f(ax)=f(x^2)\) равносильно уравнению \(ax=x^2\).
Уравнение \(x^2-ax=0\) при \(a=0\) имеет один корень \(x=0\), а при \(a\ne 0\) имеет два различных корня \(x_1=0\) и \(x_2=a\).
Нам нужно найти значения \(a\), при которых уравнение будет иметь не менее двух корней, учитывая также то, что \(a>0\).
Следовательно, ответ: \(a\in (0;+\infty)\).
\((0;+\infty)\).
Найдите все значения параметра \(a\), при каждом из которых уравнение \[2^{ax-\sqrt{x+1}}\cdot \log_{\frac{1}{3}}{\sqrt{ax+2}}+\log_9{(\sqrt{x+1}+2)}=0\]
имеет единственное решение.
Домножим правую и левую части уравнения на \(2^{\sqrt{x+1}}\) (т.к. \(2^{\sqrt{x+1}}>0\)) и перепишем уравнение в виде: \[2^{ax}\cdot \log_{\frac{1}{9}}{(ax+2)}=2^{\sqrt{x+1}}\cdot \log_{\frac{1}{9}}{(\sqrt{x+1}+2)}\]
Рассмотрим функцию \(y=2^t\cdot \log_{\frac{1}{9}}{(t+2)}\) при \(t\geqslant 0\) (т.к. \(\sqrt{x+1}\geqslant 0\)).
Производная \(y'=\left( -2^t\cdot \log_9{(t+2)}\right)'=-\dfrac{2^t}{\ln9}\cdot \left( \ln 2\cdot \ln{(t+2)}+\dfrac{1}{t+2}\right)\).
Т.к. \(2^t>0, \ \dfrac{1}{t+2}>0, \ \ln{(t+2)}>0\) при всех \(t\geqslant 0\), то \(y'<0\) при всех \(t\geqslant 0\).
Следовательно, при \(t\geqslant 0\) функция \(y\) монотонно убывает.
Уравнение можно рассматривать в виде \(y(t)=y(z)\), где \(z=ax, t=\sqrt{x+1}\). Из монотонности функции следует, что равенство возможно только в том случае, если \(t=z\).
Значит, уравнение равносильно уравнению: \(ax=\sqrt{x+1}\), которое в свою очередь равносильно системе: \[\begin{cases} a^2x^2-x-1=0\\ ax \geqslant 0 \end{cases}\]
При \(a=0\) система имеет одно решение \(x=-1\), которое удовлетворяет условию \(ax\geqslant 0\).
Рассмотрим случай \(a\ne 0\). Дискриминант первого уравнения системы \(D=1+4a^2>0\) при всех \(a\). Следовательно, уравнение всегда имеет два корня \(x_1\) и \(x_2\), причем они разных знаков (т.к. по теореме Виета \(x_1\cdot x_2=-\dfrac{1}{a^2}<0\)).
Это значит, что при \(a<0\) условию \(ax\geqslant 0\) подходит отрицательный корень, при \(a>0\) условию подходит положительный корень. Следовательно, система всегда имеет единственное решение.
Значит, \(a\in \mathbb{R}\).
\(a\in \mathbb{R}\).
Найдите все значения параметра \(a\), при каждом из которых уравнение \[2x^3-3x(ax+x-a^2-1)-3a-a^3=0\]
имеет хотя бы один корень из отрезка \([-1;0]\).
Рассмотрим функцию \(f(x)=2x^3-3x(ax+x-a^2-1)-3a-a^3\) при некотором фиксированном \(a\). Найдем ее производную: \(f'(x)=6x^2-6ax-6x+3a^2+3=3(x^2-2ax+a^2+x^2-2x+1)=3((x-a)^2+(x-1)^2)\).
Заметим, что \(f'(x)\geqslant 0\) при всех значениях \(x\) и \(a\), причем равна \(0\) только при \(x=a=1\). Но при \(a=1\):
\(f'(x)=6(x-1)^2 \Rightarrow f(x)=2(x-1)^3 \Rightarrow\) уравнение \(2(x-1)^3=0\) имеет единственный корень \(x=1\), не удовлетворяющий условию. Следовательно, \(a\) не может быть равно \(1\).
Значит, при всех \(a\ne 1\) функция \(f(x)\) является строго возрастающей, следовательно, уравнение \(f(x)=0\) может иметь не более одного корня. Учитывая свойства кубической функции, график \(f(x)\) при некотором фиксированном \(a\) будет выглядеть следующим образом:
Значит, для того, чтобы уравнение имело корень из отрезка \([-1;0]\), необходимо: \[\begin{cases} f(0)\geqslant 0\\ f(-1)\leqslant 0 \end{cases} \Rightarrow \begin{cases} a(a^2+3)\leqslant 0\\ (a+2)(a^2+a+4)\geqslant 0 \end{cases} \Rightarrow \begin{cases} a\leqslant 0\\ a\geqslant -2 \end{cases} \Rightarrow -2\leqslant a\leqslant 0\]
Таким образом, \(a\in [-2;0]\).
\(a\in [-2;0]\).
Найдите все значения параметра \(a\), при каждом из которых уравнение \[(\sin^2x-5\sin x-2a(\sin x-3)+6)\cdot (\sqrt2a+8x\sqrt{2x-2x^2})=0\]
имеет корни.
(Задача от подписчиков)
ОДЗ уравнения: \(2x-2x^2\geqslant 0 \quad\Leftrightarrow\quad x\in [0;1]\). Следовательно, для того, чтобы уравнение имело корни, нужно, чтобы хотя бы одно из уравнений \[\sin^2x-5\sin x-2a(\sin x-3)+6=0 \quad {\small{\text{или}}}\quad \sqrt2a+8x\sqrt{2x-2x^2}=0\] имело решения на ОДЗ.
1) Рассмотрим первое уравнение \[\sin^2x-5\sin x-2a(\sin x-3)+6=0 \quad\Leftrightarrow\quad
\left[\begin{gathered}\begin{aligned}
&\sin x=2a+2\\
&\sin x=3\\
\end{aligned} \end{gathered}\right. \quad\Leftrightarrow\quad \sin x=2a+2\] Данное уравнение должно иметь корни на \([0;1]\). Рассмотрим окружность:
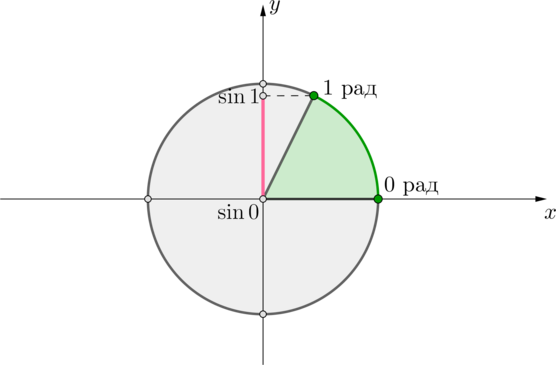
Таким образом, мы видим, что для любых \(2a+2\in [\sin 0;\sin 1]\) уравнение будет иметь одно решение, а для всех остальных – не будет иметь решений. Следовательно, при \(a\in \left[-1;-1+0,5\sin 1\right]\) уравнение имеет решения.
2) Рассмотрим второе уравнение \[\sqrt2a+8x\sqrt{2x-2x^2}=0 \quad\Leftrightarrow\quad 8x\sqrt{x-x^2}=-a\]
Рассмотрим функцию \(f(x)=8x\sqrt{x-x^2}\). Найдем ее производную: \[f'(x)=-4\cdot \dfrac{x(4x-3)}{\sqrt{x-x^2}}\] На ОДЗ производная имеет один ноль: \(x=\frac34\), который к тому же является точкой максимума функции \(f(x)\).
Заметим, что \(f(0)=f(1)=0\). Значит, схематично график \(f(x)\) выглядит так:
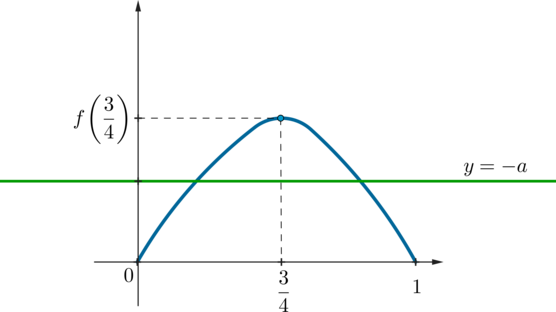
Следовательно, для того, чтобы уравнение имело решения, нужно, чтобы график \(f(x)\) пересекался с прямой \(y=-a\) (на рисунке изображен один из подходящих вариантов). То есть нужно, чтобы \[0\leqslant -a\leqslant f\left(\dfrac34\right) \quad\Rightarrow\quad -\dfrac{3\sqrt3}2\leqslant a\leqslant 0\]
3) Таким образом, изначальное уравнение будет иметь решения при \(a\in \left[-1;-1+0,5\sin 1\right]\) или \(a\in \left[-\dfrac{3\sqrt3}2;0\right]\). Объединяя эти решения, получим \[a\in \left[-\dfrac{3\sqrt3}2;0\right].\]
\(a\in \left[-\dfrac{3\sqrt3}2;0\right]\)
Найдите все значения параметра \(a\), при каждом из которых уравнение \[\sqrt{x-1}+5x^2-9x+3a+8=\dfrac{a^2}{x}\]
имеет ровно одно решение.
Рассмотрим семейства функций \(f_a(x)=\sqrt{x-1}+5x^2-9x+3a+8, \ \ g_a(x)=\dfrac{a^2}{x}\).
ОДЗ уравнения: \(x\geqslant 1\). При этих \(x\):
Функция \(y_1=\sqrt{x-1}\) является строго возрастающей. Графиком функции \(y_2=5x^2-9x\) является парабола, вершина которой находится в точке \(x=\dfrac{9}{10}\). Следовательно, при всех \(x\geqslant 1\) функция \(y_2\) также строго возрастает (правая ветвь параболы). Т.к. сумма строго возрастающих функций есть строго возрастающая, то \(f_a(x)\) – строго возрастает (константа \(3a+8\) не влияет на монотонность функции).
Функция \(g_a(x)=\dfrac{a^2}{x}\) при всех \(x\geqslant 1\) представляет собой часть правой ветви гиперболы и является строго убывающей.
Решить уравнение \(f_a(x)=g_a(x)\) — значит найти точки пересечения функций \(f\) и \(g\). Из их противоположной монотонности следует, что уравнение может иметь не более одного корня.
При \(x\geqslant 1\) \(f_a(x)\geqslant 3a+4, \ \ \
0<g_a(x)\leqslant a^2\). Следовательно, уравнение будет иметь единственное решение в том случае, если: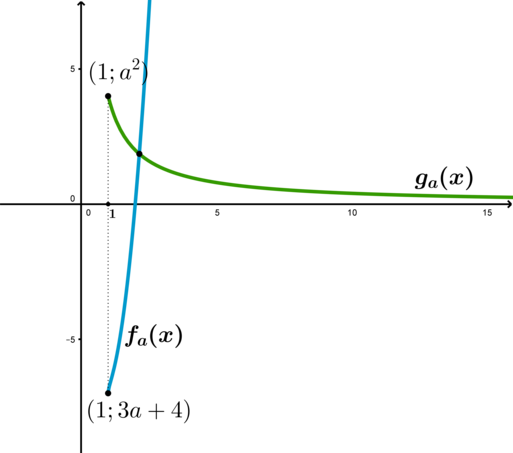
\[3a+4\leqslant a^2 \Rightarrow a\in (-\infty;-1]\cup[4;+\infty)\]
\(a\in (-\infty;-1]\cup[4;+\infty)\).
Подготовка к Единому государственному экзамену по математике зачастую вызывает особые затруднения у выпускников. Есть множество сложных заданий, которым уделяется недостаточно внимания в общеобразовательной программе. В их числе нахождение интервалов монотонности функций и точек экстремума. Как показывает практика последних лет, многие выпускники сталкиваются с проблемами в решении подобных заданий. Поэтому стоит сделать акцент на их повторении, чтобы легко справляться даже с задачами повышенного уровня сложности. В этом вам поможет наш онлайн-сервис.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха!
Наш образовательный портал позволит вам быстро и эффективно подготовиться к предстоящему итоговому тестированию по математике. Наши преподаватели собрали, систематизировали и оформили информацию по тематике в максимально простой и понятной форме. Поэтому ученики смогут быстро воспринимать материалы. Благодаря особому методу они уже через несколько дней будут решать даже те задания, которые казались невыполнимыми.
Начните с повторения правил и формул, которые могут понадобиться при исследовании монотонности функций. Для этого перейдите в раздел «Теоретическая справка». Вы вспомните виды и свойства функций, как определить знак производной, найти критические точки и многое другое. В каталогах представлены как типовые примеры по тематике, так и задания повышенного уровня сложности, которые могут встретиться в ЕГЭ. Их список постоянно обновляется и дополняется, поэтому выпускники будут ежедневно получать новые задания без повторений. Дети научатся находить количество значений необходимых параметров, работать с различными видами тригонометрических функций, а также справляться с уравнениями, в которых встречаются корни различной степени и логарифмы.
Если у школьника возникнут сложности с решением примера, он может добавить задание в «Избранное» и вернуться к нему позже.
Для того чтобы занятия проходили максимально результативно, советуем начать с самых простых заданий, где нужно указать промежутки монотонности функций y=f(x), и постепенно переходить к более трудным. Так ученики смогут выявить свои самые слабые стороны и сделать упор на решении конкретных типов упражнений.
Чтобы получить большие результаты, рекомендуем обращаться к нашему порталу ежедневно. Начните подготовку к итоговому тестированию уже сегодня вместе с онлайн-сервисом «Школково»!
Обучающие материалы доступны всем желающим подтянуть знания по математике. Вы можете сохранить результаты и отслеживать свой прогресс. Для этого зарегистрируйтесь в системе на нашем официальном сайте 3.shkolkovo.online.



