Кинематика (страница 3)
Готовиться с нами - ЛЕГКО!

Какую горизонтальную скорость имел самолет при сбрасывании бомбы с высоты \(h=500\) м, если она упала на расстоянии \(S=300\) м от места бросания. Ответ дайте в м/с.
Бомба будет лететь с постоянной скоростью \(v_0\) относительно оси \(Ox\) (её и нужно найти), и равноускоренно с ускорением \(g\) без начальной скорости относительно оси \(Oy\).
Запишем уравнение движения бомбы относительно \(Oy\): \[h=\dfrac{gt^2}{2}\] Выразим \(t\) (время всего полета бомбы): \[t=\sqrt{\dfrac{2h}{g}}\] Запишем уравнение движения бомбы относительно \(Ox\): \[S=v_0t\] Подставим время падения в эту формулу: \[S=v_0\cdot\sqrt{\dfrac{2h}{g}}\] Осталось выразить \(v_0\): \[v_0=S\sqrt{\dfrac{g}{2h}}=300\text{ м}\sqrt{\dfrac{10\text{ м/с$^2$}}{2\cdot 500\text{ м}}}=30\text{ м/с}\]
Тело брошено c поверхности Земли вертикально вверх с начальной скоростью \(v_0=20\) м/с. Найти:
1) Максимальную высоту подъема
2) Время подъема
3) Скорость в момент падения
Сопротивление воздуха не учитывать.
В ответ дайте 3 числа в том порядке, которые заданы в вопросе, без пробелов и точек в системе СИ, округлив результаты вычисления до целых.
Скорость тела в момент падения будет равна начальной скорости \(v_0\), т.к. в обоих положениях тело будет иметь только кинетическую энергию (следовательно, скорость в этих положениях одинакова и максимальна).
Найдем время подъема по формуле нахождения скорости при равнозамедленном движении, учитывая, что скорость тела в наивысшей точке равна 0: \[v=v_0-gt\] \[0=v_0-gt\] \[t=\dfrac{v_0}{g}=\dfrac{20\text{ м/с}}{10\text{ м/с$^2$}}=2\text{ с}\]
Найдем максимальную высоту подъема тела по формуле равнозамедленного движения: \[y=v_0t-\dfrac{gt^2}{2}\] \[y=v_0\cdot\dfrac{v_0}{g}-\dfrac{g\bigg(\dfrac{v_0}{g}\bigg)^2}{2}=\dfrac{v_0^2}{2g}=\dfrac{400\text{ м$^2$/с$^2$}}{2\cdot 10\text{ м/с$^2$}}=20\text{ м}\]
Тело бросают вертикально вверх. За небольшой промежуток времени \(t\) тело прошло путь \(S=40\) м, не меняя направления движения. За это время скорость тела уменьшилась в 3 раза. Чему равна начальная скорость тела? Ответ дайте в м/с
Запишем уравнение равнозамедленного движения и зависимость скоростей спустя время \(t\): \[S=v_0t-\dfrac{gt^2}{2}\] \[v=v_0-gt\] По условию \(v=v_0/3\), где \(v\) — скорость тела через время t. Отсюда: \[\dfrac{v_0}{3}=v_0-gt\Rightarrow t=\dfrac{2v_0}{3g}\] Подставим это в первую формулу: \[S=v_0\cdot\dfrac{2v_0}{3g}-\dfrac{g\cdot\Bigg(\dfrac{2v_0}{3g}\Bigg)^2}{2}\] Осталось выразить \(v_0\): \[v_0=\dfrac{3}{2}\cdot\sqrt{gS}=1,5\cdot\sqrt{10\text{ м/с$^2$}\cdot40\text{ м}}=30\text{ м/с}\]
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты \(Н=25\) м (см. рисунок). На краю трамплина скорость гонщика направлена под углом \(\alpha= 30^0\) к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова дальность полета L на этом трамплине? Cопротивлением воздуха и трением пренебречь. Ответ дайте в метрах и округлите до целых.
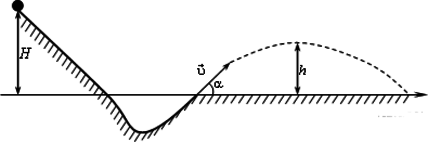
Запишем закон сохранения энергии для высоты \(H\) и для края трамплина: \[mgH=\frac{mv^2}{2}\] \[v^2=2gH\] 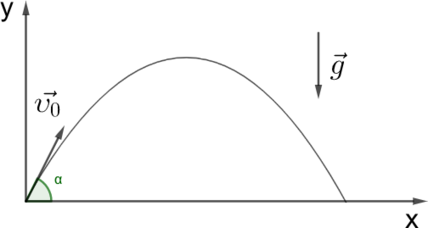
Спроецируем вектор скорости и ускорения на каждую ось: \[\upsilon_{x}=\upsilon\cos{\alpha} \quad \upsilon_{y}=\upsilon\sin{\alpha}\] \[a_x=0 \quad a_y=-g\]
Запишем уравнение движения и зависимость скоростей на каждую ось: \[x=x_0+\upsilon_{0x}t+\frac{a_xt^2}{2}\] \[y=y_0+\upsilon_{0y}t+\frac{a_yt^2}{2}\] \[\upsilon_{x}=\upsilon_{0x}+a_xt\] \[\upsilon_{y}=\upsilon_{0y}+a_yt\] С учетом начальных условий получаем: \[x=\upsilon\cos{\alpha}t\] \[y=\upsilon\sin{\alpha}t-\frac{gt^2}{2}\] Когда гонщик приземлится, \(y=0\): \[0=\upsilon_0\sin{\alpha}t-\frac{gt^2}{2}\] \[t=\frac{2v_0\sin\alpha}{g}\]
Найдем дальность полета \(L\): \[L=x=\upsilon_0\cos{\alpha}t=\upsilon_0\cos{\alpha}\frac{2v_0\sin\alpha}{g}=\frac{v^2_0\sin2\alpha}{g}\] Подставим сюда первую формулу: \[L=\frac{2gH\sin2\alpha}{g}=2H\sin2\alpha=2H\sin60^{\circ}=H\sqrt{3}=25\text{ м}\cdot \sqrt{3}\approx 43\text{ м}\]
Тело брошено под углом \(\alpha=30^\circ\) к горизонту со скоростью \(\upsilon_0=10\) м/с. Сопротивлением воздуха пренебречь.
Найдите:
1) Время полета \(t\)
2) Дальность полета \(x_m\)
3) Максимальную высоту подъема \(y_m\)
В ответ дайте 3 числа в том порядке, которые заданы в вопросе, без пробелов и точек в системе СИ, округлив результаты вычисления до целых.
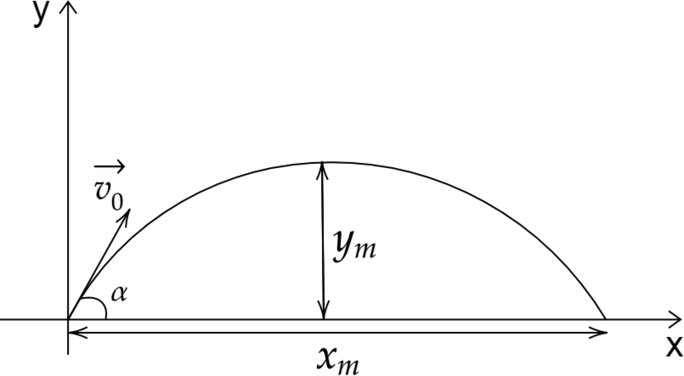
Спроецируем вектор скорости и ускорения на каждую ось: \[\upsilon_{0x}=\upsilon_0\cos{\alpha} \quad \upsilon_{0y}=\upsilon_0\sin{\alpha}\] \[a_x=0 \quad a_y=-g\]
Запишем уравнение движения и зависимость скоростей на каждую ось: \[x=x_0+\upsilon_{0x}t+\frac{a_xt^2}{2}\] \[y=y_0+\upsilon_{0y}t+\frac{a_yt^2}{2}\] \[\upsilon_{x}=\upsilon_{0x}+a_xt\] \[\upsilon_{y}=\upsilon_{0y}+a_yt\] С учетом начальных условий законы движения тела имеют вид: \[x=\upsilon_0 \cos\alpha t\] \[y=\upsilon_0 \sin\alpha t-\frac{g t^2}{2}\]
В момент приземления \(y=0\), \(x=x_m\): \[0=\upsilon_0 \sin\alpha t-\frac{g t^2}{2} \Rightarrow t=\frac{2\upsilon_0\sin{\alpha}}{g}=\dfrac{2\cdot 10\text{ м/с}\cdot 0,5}{10\text{ м/с$^2$}}=1\] \[x_m=\upsilon_0 \cos\alpha t=\upsilon_0 \cos\alpha\cdot \dfrac{2\upsilon_0\sin{\alpha}}{g}=\dfrac{v_0^2\sin2\alpha}{g}=\dfrac{100\text{ м$^2$/с$^2$}\cdot \dfrac{\sqrt{3}}{2}}{10\text{ м/с$^2$}}\approx9\text{ м}\]
\(t_2=\dfrac{t}{2}=\dfrac{v_0\sin\alpha}{g}\) — время, за которое тело поднимется на максимальную высоту \(y_m\).
\[y_m=v_0\sin\alpha t_2-\dfrac{gt_2^2}{2}=v_0\sin\alpha\cdot\dfrac{v_0\sin\alpha}{g}-\dfrac{g\cdot\bigg(\dfrac{v_0\sin\alpha}{g}\bigg)^2}{2}=\dfrac{v_0^2\sin^2\alpha}{2g}=\dfrac{2\cdot 100\text{ м$^2$/с$^2$}\cdot 0,25}{2\cdot 10\text{ м/с$^2$}}=1,25\text{ м}\]
Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен \(30^{\circ}\). На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с. Ответ дайте в метрах.
Введем систему координат. При упругом ударе угол падения равен углу отражения. Угол падения равен углу наклона плоскости (из геометрии), следовательно, равен \(30^{\circ}\). Из этого следует, что после удара угол между вектором скорости и поверхностью наклонной плоскости равен \(\beta=2\alpha=60^{\circ}\). 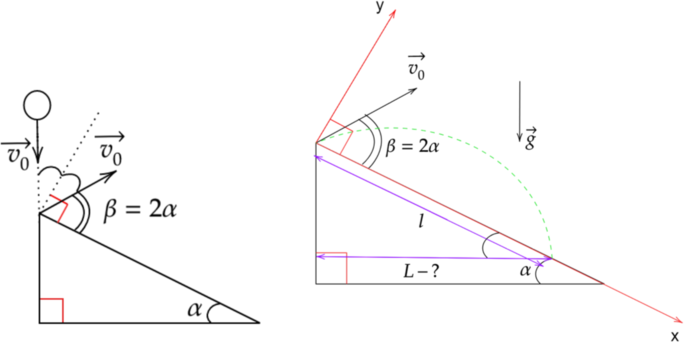
Спроецируем вектор скорости и ускорения на каждую ось: \[\upsilon_{0x}=\upsilon_0\sin{\alpha} \quad \upsilon_{0y}=\upsilon_0\cos{\alpha}\] \[a_x=g\sin\alpha \quad a_y=-g\cos\alpha\]
Законы движения шарика имеют вид: \[x=\upsilon_0 \sin\alpha t+\frac{g\sin\alpha t^2}{2}\] \[y=\upsilon_0 \cos\alpha t-\frac{g\cos\alpha t^2}{2}\]
В момент второго соударения \(y=0\), \(x=l\): \[l=\upsilon_0 \sin\alpha t+\frac{g\sin\alpha t^2}{2}\] \[0=\upsilon_0 \cos\alpha t-\frac{g\cos\alpha t^2}{2} \Rightarrow t=\frac{2\upsilon_0}{g}=\dfrac{2\cdot 1\text{ м/с}}{10\text{ м/с$^2$}}=0,2~c\]
Из рисунка видно, что \(L=l\cos\alpha\) \[L=\cos\alpha\Bigg(\upsilon_0 \sin\alpha t+\frac{g\sin\alpha t^2}{2}\Bigg)=\dfrac{\sqrt{3}}{2}\cdot\Bigg(1\text{ м/с}\cdot0,5\cdot0,2~c+\dfrac{10\text{ м/с$^2$}\cdot0,5\cdot(0,2~c)^2}{2}\Bigg)\approx0,17 \text{ м}\]
В безветренную погоду самолет затрачивает на перелет между городами \(t_1=6\) часов. Если во время полета дует боковой ветер со скоростью \(V=20\) м/с перпендикулярно линии полета, то самолет затрачивает на перелет на несколько минут больше. Определите, на какое время увеличивается время полета, если скорость самолета относительно воздуха постоянна и равна \(v=100\) м/с. Ответ дать в минутах.
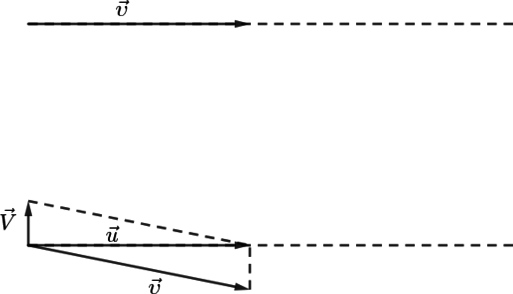
Путь, пройденный самолетом в первом случае: \[L=\upsilon t_1\] Закон сложения скоростей в векторном виде для перелета во время ветра: \[\vec{u}=\vec{\upsilon}+\vec{V}\]
По теореме Пифагора: \[u=\sqrt{\upsilon^2-V^2}\]
Тогда путь, пройденный самолетом во втором случае (равен пути в первом случае): \[L=ut_2=\sqrt{\upsilon^2-V^2} t_2=vt_1\] Отсюда: \[t_2=\frac{\upsilon t_1}{\sqrt{\upsilon^2-V^2}}=\frac{100\text{ м/с}\cdot6\cdot 3600~c}{\sqrt{(100\text{м/с})^2-(20\text{ м/с})^2}}\approx4140~c\]
Тогда разница во времени \[\Delta t=t_2-t_1=4140~c - 3600~c = 540~c\approx 9\text{ мин}\]



