Электрический ток. Закон Ома (страница 2)
Готовиться с нами - ЛЕГКО!

Электрический ток — это направленное движение заряженных частиц, при котором происходит перенос заряда из одних областей пространства в другие.
Сила тока — количественная характеристика электрического тока. В случае постоянного тока абсолютная величина силы тока есть отношение абсолютной величины заряда \(q\), прошедшего через поперечное сечение проводника за время \(t\), к этому времени. \[I=\dfrac{q}{t}\]
Единицы измерения: \(\displaystyle [\text{А}]\) (Ампер).
Электродвижущая сила (ЭДС)
Сторонняя сила \(\vec{F}_\text{ст}\) не имеет отношения к стационарному электрическому полю.
\[\mathscr{E}=\dfrac{A_\text{ст}}{q}\]
Данная величина называется электродвижущей силой (ЭДС) источника тока.
Единицы измерения: \(\displaystyle [\text{В}]\) (Вольт).
Электрическое напряжение между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Единицы измерения: \(\displaystyle [\text{В}]\) (Вольт).
Закон Ома для участка цепи
\[I=\dfrac{U}{R}\]
Омическое сопротивление \(R\) — сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии постоянного тока.
Единицы измерения: \(\displaystyle [\text{Ом}]\) (Ом).
Удельное сопротивление
Сопротивление проводника прямо пропорционально его длине \(l\) и обратно пропорционально площади поперечного сечения \(S\):
\[R=\rho\dfrac{l}{S}\]
Коэффициент пропорциональности \(\rho\) — удельное сопротивление данного вещества.
Единицы измерения: \(\displaystyle [\text{Ом}\cdot\text{м}]\) (Ом на метр).
Зависимость удельного сопротивления от температуры
\[\rho=\rho_0(1+\alpha t)\]
Множитель \(\alpha\) называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.
\(\rho_0\) — удельное сопротивление проводника при \(0^oC\).
Последовательное и параллельное соединение проводников
Последовательное соединение проводников
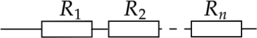
\[I=I_1=I_2=...=I_n\]
\[U=U_1+U_2+...+U_n\]
\[R=R_1=R_2=...=R_n\]
Параллельное соединение проводников
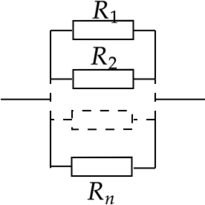
\[I=I_1+I_2+...+I_n\]
\[U=U_1=U_2=...=U_n\]
\[\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+...+\dfrac{1}{R_n}\]
Закон Ома для полной цепи
Сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма внешних и внутренних сопротивлений.
\[I=\dfrac{\mathscr{E}}{R+r}\]
Работа тока
\[A=Uq=UIt\]
Единицы измерения: \(\displaystyle [\text{Дж}]\) (Джоуль).
Мощность тока — отношение работы тока ко времени, за которое эта работа совершена.
\[P=\dfrac{A}{t}\]
Единицы измерения: \(\displaystyle [\text{Вт}]\) (Ватт).
Закон Джоуля-Ленца
Пусть на рассматриваемом участке цепи не совершается механическая работа и не протекают химические реакции. Работа поля \(A\) целиком превращается в тепло \(Q=A\).
\[Q=UIt=I^2Rt=\dfrac{U^2}{R}t\]
Первое правило Кирхгофа
Алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю.
Также можно легко запомнить первый закон Кирхгофа следующим образом: сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
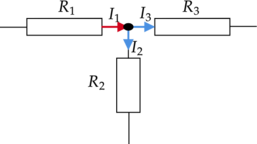
Здесь ток \(I_1\) — ток, втекающий в узел, а токи \(I_2\) и \(I_3\) — токи, вытекающие из узла. Тогда можно записать:
\(I_1 = I_2 + I_3,\ (1)\)
Перенесем токи \(I_2\) и \(I_3\) в левую часть выражения (1), тем самым получим:
\(I_1 - I_2 - I_3 = 0,\ (2)\)
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «—».
Второе правило Кирхгофа
Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.
Термин «алгебраическая сумма» означает, что как величина ЭДС, так и величина падения напряжения на элементах может быть как со знаком «+», так и со знаком «—». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта: либо по часовой стрелке, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура, записываются со знаком «+», в противном случае ЭДС записываются со знаком «—».
— напряжения, падающие на элементах цепи, записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «—».
Например, рассмотрим цепь на рисунке и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке и выбрав направление токов через резисторы, как показано на рисунке.
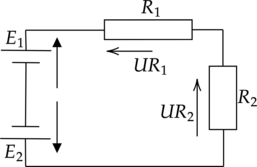
Получим:
\(E_1- E_2 = -UR_1 - UR_2\) или \(E_1 = E_2 - UR_1 - UR_2\)
В сеть с постоянным напряжением \(U_o\) = 120 В включены три одинаковых сопротивления: два параллельно, а одно последовательно с ними. Определите напряжение на параллельно соединенных сопротивлениях. (Ответ дайте в вольтах.)
Общее сопротивление всей цепи: \[R_{\text{ общ}}=R+\dfrac{R}{2}=1,5R\] По закону Ома ток в цепи равен: \[I_o=\dfrac{U_o}{1,5R}\] Напряжение на параллельно соединенных сопротивлениях: \[U=I_o\dfrac{R}{2}=\dfrac{U_o}{1,5 R}\cdot\dfrac{R}{2}=\dfrac{U_o}{3}\] \[U=\dfrac{120\text{ В}}{3}=40 \text{ В}\]
Электрическая плитка включена в сеть с напряжением 60 В с помощью проводов, имеющих некоторое сопротивление. При этом напряжение на плитке равно 40 В. Чему будет равно напряжение на плитке, если к ней подключить последовательно такую же плитку? (Ответ дайте в вольтах.)
Исходя из закона Ома можно вывести, что напряжение равно: \[\; \; \; \; U=IR\; \; \; \; (1)\] где \(I\) — сила тока, \(R\) — сопротивление.
Для первого случая можем записать: \[U_o=U_r+U_p\] где \(U_o\) — общее напряжение цепи, \(U_r\) — напряжение проводов, \(U_p\) — напряжение плитки.
Напряжение на проводах 20 В, на плитке 40 В. Сила тока одинаковая, следовательно, сопротивление плитки в 2 раза больше сопротивления проводов: \(R=2r\) по формуле (1).
Для второго случая закон Ома для полной цепи: \[I=\dfrac{U_o}{R+R+r}=\dfrac{U_o}{2,5 R}\] Напряжение на плитке: \[U_2=IR=\dfrac{U_oR}{2,5R}\] \[U_2 = \dfrac{60\text{ В}}{2,5} =24 \text{ В}\]
Если к батарее с ЭДС 3 В и внутренним сопротивлением 2 Ом накоротко подсоединить амперметр, то он покажет силу тока 1 А. Определите сопротивление амперметра. (Ответ дайте в омах.)
Закон Ома для полной цепи: \[I=\dfrac{\varepsilon}{R_a+r}\] где \(I\) — сила тока, \(\varepsilon\) — ЭДС источника, \(R_a\) — внешнее сопротивление (амперметра), \(r\) — внутреннее сопротивление.
Тогда сопротивление амперметра: \[R_a=\dfrac{\varepsilon}{I}-r\] \[R_a = \dfrac{3\text{ В}}{1\text{ А}}-2\text{ Ом}=1 \text{ Ом}\]
В цепи, состоящей из источника тока с ЭДС 6 В и внутренним сопротивлением 2 Ом и реостата, идет ток силой 1 А. Какова будет сила тока в цепи, если сопротивление реостата уменьшить в 2 раза? (Ответ дайте в амперах.)
Закон Ома для полной цепи: \[I=\dfrac{\varepsilon}{R_1+r}\] где \(I\) — сила тока, \(\varepsilon\) — ЭДС источника, \(R_1\) — внешнее сопротивление (реостата), \(r\) — внутреннее сопротивление.
Тогда сопротивление реостата равно: \[R_1=\dfrac{\varepsilon}{I}-r=\dfrac{6\text{ В}}{1\text{ А}}-2\text{ Ом}=4 \text{ Ом}\] Уменьшим сопротивление реостата в 2 раза \(R_2=2\) Ом.
Закон Ома для полной цепи: \[I=\dfrac{\varepsilon}{R_2+r}=\dfrac{6\text{ В}}{2\text{ Ом}+2\text{ Ом}}=1,5 \text{ А}\]
К источнику тока с ЭДС \(\xi=4\) В и внутренним сопротивлением \(r=5\) Ом подсоединили нагрузочное сопротивление. Чему оно должно быть равно, чтобы КПД источника был равен 50 %? (Ответ дайте в омах.)
КПД цепи: \[\eta=\frac{IUt}{I\xi t}= \frac{U}{\xi },\] где \(I\) – сила тока, \(U\) – напряжение,\(t\) – время. Выразим напряжение на напряжение на нагрузке \[U_R=\eta \xi=2 \text{ В}\] \[I=\frac{\xi}{R+r}=\frac{U}{R}\] \[2R=R+r\] \[R=r=5 \text{ Ом}\]
Какой заряд пройдет по проводнику сопротивлением 10 Ом за время 20 с, если к его концам приложено напряжение 24 В? (Ответ дайте в кулонах.)
Сила тока по определению равна: \[\; \; \; \; I=\dfrac{\Delta q}{\Delta t} \; \; \; \; (1)\] где \(\Delta q\) — заряд, прошедший за время \(\Delta t\).
Также по закону Ома: \[\; \; \; \; I = \dfrac{U}{R} \; \; \; \; (2)\] где \(U\) — напряжение, \(R\) — сопротивление проводика.
Приравняем (1) и (2): \[\dfrac{\Delta q}{\Delta t} = \dfrac{U}{R}\] Тогда заряд, который пройдет по проводнику, равен: \[\Delta q=\dfrac{U \Delta t}{R}\] \[\Delta q =\dfrac{24\text{ В}\cdot20\text{ с}}{10\text{ Ом}}=48 \text{ Кл}\]


