Электрический ток
Готовиться с нами - ЛЕГКО!

На графике представлены результаты измерений напряжения \(U\) на реостате при различных значениях сопротивления \(R\) реостата. Погрешность измерения напряжения \(\Delta U = \pm 0,2\) В, сопротивления \(\Delta R = \pm 0,4\) Ом. 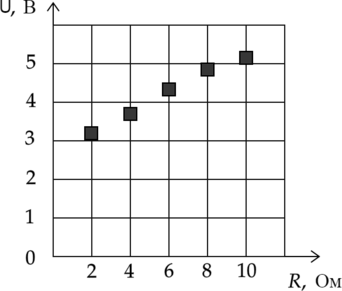
Выберете два верных утверждения на основании данных графика.
1) С увеличением сопротивления напряжение увеличивается.
2) При сопротивлении 2 Ом сила тока примерно равна 1,5 А.
3) При сопротивлении 1 Ом сила тока в цепи примерно равна 2 А.
4) При сопротивлении 8 Ом сила тока примерно равна 0,78 А.
5) Напряжение не зависит от сопротивления.
1) \(\color{green}{\small\text{Верно }}\)
Исходя из графика, можно сделать вывод, что чем больше сопротивление реостата, тем больше напряжение на нем.
2) \(\color{green}{\small\text{Верно }}\)
По закону Ома сила тока в реостате прямо пропорциональна напряжению и обратно пропорциональна сопротивлению: \[I = \dfrac{U}{R}\] При сопротивлении 2 Ом напряжение на реостате равно \(3\) В. Тогда сила тока примерно равна: \[I= \dfrac{3\text{ В}}{2\text{ Ом}} = 1,5\text{ А}\] 3) \(\color{red}{\small\text{Неверно }}\)
Информации на графике недостаточно, чтобы сделать вывод, чему равна сила тока, протекающего через реостат, при сопротивлении 1 Ом.
4) \(\color{red}{\small\text{Неверно }}\)
При сопротивлении 8 Ом сила тока примерно равна: \[I= \dfrac{4,8\text{ В}}{8\text{ Ом}} = 0,6\text{ А}\] 5) \(\color{red}{\small\text{Неверно }}\)
Исходя из графика видно, что напряжение на реостате зависит от сопротивления.
На рисунке изображена зависимость силы тока через лампу накаливания от приложенного к ней напряжения.
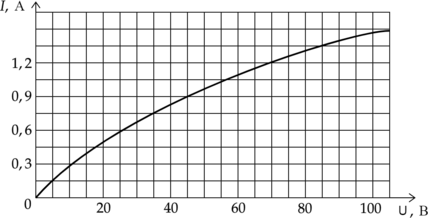
Выберите два верных утверждения на основании данных графика.
1) Сопротивление лампы увеличивается при увеличении силы тока.
2) Мощность, выделяемая в лампе при напряжении 55 В, равна 70 Вт.
3) Мощность, выделяемая в лампе при напряжении 85 В, равна 114,75 Вт.
4) Сопротивление лампы при силе тока в ней 1,05 А равно 100 Ом.
5) Мощность, выделяемая на лампе, при увеличении силы тока уменьшается.
1) \(\color{green}{\small\text{Верно }}\)
Сопротивление лампы увеличивается при увеличении силы тока.
2) \(\color{red}{\small\text{Неверно }}\)
Мощность, выделяемую на лампе, можно найти по формуле: \[N = IU\] При напряжении 55 В сила тока в лампе равна 1,05 А. Мощность, выделяемая на ней, равна: \[N = 1,05\text{ А} \cdot 55\text{ В} = 57,75\text{ Вт}\] 3) \(\color{green}{\small\text{Верно }}\)
При напряжении 85 В сила тока в лампе равна 1,35 А. Мощность, выделяемая на ней, равна: \[N = 1,35\text{ А} \cdot 85\text{ В} = 114,75\text{ Вт}\] 4) \(\color{red}{\small\text{Неверно }}\)
Сопротивление лампы можно выразить из закона Ома: \[I = \dfrac{U}{R} \; \; \; \Rightarrow \; \; \; R=\dfrac{U}{I}\] При силе тока 1,05 А напряжение равно 55 В. Сопротивление лампы равно: \[R = \dfrac{55\text{ В}}{1,05\text{ А}} \approx 52 \text{ Ом}\] 5) \(\color{red}{\small\text{Неверно }}\)
Мощность, выделяемая на лампе, при увеличении силы тока увеличивается.
На рисунке изображена цепь состоящая из конденсатора, источника тока, ключа и резистора с сопротивлением \(R=30\) кОм. В начальный момент времени (\(t=0\)) ключ \(K\) замкнули, при этом конденсатор полностью разряжен. Результаты измерения силы тока представлены в таблице 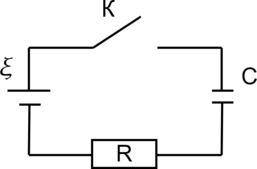
\[\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
t \text{ с}&0&1&2&3&4&5&6\\
\hline
I\text{ мкА}&100&50&30&20&10&5&1\\
\hline
\end{array}\] Выберите два верных утверждения о данной ситуации и укажите их номера.
1) Ток через резистор в процессе наблюдения уменьшается.
2) Через 5 с после замыкания ключа конденсатор полностью зарядился.
3) ЭДС источника тока составляет 6 В.
4) В момент времени t = 3 с напряжение на резисторе равно 0,6 В.
5) В момент времени t = 3 с напряжение на резисторе равно 0,9 В.
1) \(\color{green}{\small\text{Верно }}\)
Из таблицы видно, что сила тока со временем уменьшается, а значит первое утверждение верно.
2) \(\color{red}{\small\text{Неверно }}\)
Через 5 секунд ток в цепи еще не равен 0, а это значит, что конденсатор еще не зарядился до конца.
3) \(\color{red}{\small\text{Неверно }}\)
ЭДС источника равен силе тока в начальный момент, так как тогда конденсатор еще не зарядился, умножить сопротивление резистора по закону Ома \[\xi=I_1 R= 100\text{ мкА}\cdot 30\text{ кОм}=3\text{ В}\] ЭДС не равно 6 В, а значит 3) неверно
4) \(\color{green}{\small\text{Верно }}\)
По закону Ома \[U_3=I_3R= 20\text{ мкА}\cdot 30\text{ кОм}=0,6\text{ В}\] Сопротивление на резисторе равно 0,6 В, значит, 4) верно
\(\color{red}{\small\text{Неверно }}\)
По пункту 4) пункт 5) будет неверным
На рисунке изображена цепь состоящая из конденсатора, источника тока, ключа и резистора с сопротивлением \(R=30\) кОм. В начальный момент времени (\(t=0\)) ключ \(K\) замкнули, при этом конденсатор полностью разряжен. Результаты измерения силы тока представлены в таблице 
\[\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
t \text{ с}&0&1&2&3&4&5&6\\
\hline
I\text{ мкА}&100&50&30&20&10&5&1\\
\hline
\end{array}\] Выберите два верных утверждения о данной ситуации и укажите их номера.
1) Ток через резистор в процессе наблюдения увеличивается.
2) Через 2 с после замыкания ключа конденсатор еще полностью разряжен.
3) ЭДС источника тока составляет 3 В.
4) В момент времени t = 3 с напряжение на резисторе равно 0,27 В.
5) В момент времени t = 3 с напряжение на конденсаторе равно 2,1 В.
1) \(\color{red}{\small\text{Неверно }}\)
Из таблицы видно, что сила тока со временем уменьшается, а значит первое утверждение неверно.
2) \(\color{red}{\small\text{Неверно }}\)
На конденсаторе будет возникать напряжение, которое будет противоположное направлению движению тока, а так как сила тока в цепи при \(t=2\) меньше, чем сила тока при \(t=0\), то конденсатор будет заряжен.
3) \(\color{green}{\small\text{Верно }}\)
ЭДС источника равен силе тока в начальный момент, так как тогда конденсатор еще не зарядился, умножить сопротивление резистора по закону Ома \[\xi=I_1 R= 100\text{ мкА}\cdot 30\text{ кОм}=3\text{ В}\] ЭДС равно 3 В, а значит 3) верно
4) \(\color{red}{\small\text{Неверно }}\)
По закону Ома \[U_3=I_3R= 30\text{ мкА}\cdot 30\text{ кОм}=0,9\text{ В}\] Сопротивление на резисторе равно 0,9 В, значит, 4) неверно
5) \(\color{green}{\small\text{Верно }}\)
Напряжение на конденсаторе будет равно разности между ЭДС источника и напряжением на резисторе, а значит оно равно \[U_C=\xi-I_3R=3\text{ В}-0,9\text{ В}=2,1\text{ В}\] Напряжение равно 2,1 В, что означает, что 5) верно.
В колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменялся заряд в зависимости от времени \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}
\hline
t \text{ мкс}&0&1&2&3&4&5&6&7&8&9\\
\hline
q\text{ нКл}&4&2&0&-2&-4&-2&0&2&4&2\\
\hline
\end{array}\] Выберите два верных утверждения о данной ситуации и укажите их номера.
1) Период колебаний равен \(4\cdot10^{−6} c\).
2) В момент \(t = 2\cdot 10^{−6} c\) энергия катушки максимальна.
3) В момент \(t = 4\cdot 10^{−6} c\) энергия конденсатора минимальна.
4) В момент \(t = 2\cdot 10^{−6} c\) сила тока в контуре равна 0.
5) Частота колебаний равна 125 кГц.
1) \(\color{red}{\small\text{Неверно }}\)
Период колебаний это время, между двумя последовательными одинаковыми величинами заряда. Возьмем \(q=4\text{ нКл}\) в первый раз он был при \(t=0\text{ мкс}\), а второй раз при \(t=8\text{ мкс}\), а значит период равен 8 мкс, то есть \(8 \cdot 10^{-6}\) с.
2) \(\color{green}{\small\text{Верно }}\)
Энергия катушки будет максимальна, когда энергия конденсатора будет минимальна, а это наступает при минимальном по модулу заряде (\(W=\dfrac{q^2}{2C}\)). У нас заряд по модулю минимален при \(t = 2\cdot 10^{−6} c\) и \(t = 6\cdot 10^{−6} c\). Значит энергия катушки при \(t = 2\cdot 10^{−6} c\) максимальна.
3) \(\color{red}{\small\text{Неверно }}\)
Энергия конденсатор будет зависит от заряда на его пластинах, когда заряд на конденсаторе по модулю будет максимален , то и энергия конденсатора будет максимальна \(W=\dfrac{q^2}{2C}\), при \(t = 4\cdot 10^{−6} c\) заряд по модулю максимален, следовательно, энергия на конденсаторе максимальна.
4) \(\color{red}{\small\text{Неверно }}\)
Заряд в контуре изменяется синусоидально. А так как сила тока производная от заряда, то сила тока будет максимальна при минимальном по модулю заряде, то есть при \(t=0\), \(t = 4\cdot 10^{−6} c\) и \(t = 8\cdot 10^{−6} c\). Значит при \(t = 2\cdot 10^{−6} c\) максимальная сила тока.
5) \(\color{green}{\small\text{Верно }}\)
Частота \(\nu=\dfrac{1}{T}=\dfrac{1}{8\cdot 10^{-6}\text{ с}}=125\text{ кГц}\)
В колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменялся заряд в зависимости от времени \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}
\hline
t \text{ мкс}&0&1&2&3&4&5&6&7&8&9\\
\hline
q\text{ нКл}&4&2&0&-2&-4&-2&0&2&4&2\\
\hline
\end{array}\] Выберите два верных утверждения о данной ситуации и укажите их номера.
1) Период колебаний равен \(8\cdot10^{−6} c\).
2) В момент \(t = 2\cdot 10^{−6} c\) энергия катушки минимальна.
3) В момент \(t = 4\cdot 10^{−6} c\) сила тока в контуре будет минимальна.
4) В момент \(t =4 \cdot 10^{−6} c\) сила тока в контуре равна будет максимальна.
5) Частота колебаний равна 250 кГц.
1) \(\color{green}{\small\text{Верно }}\)
Период колебаний это время, между двумя последовательными одинаковыми величинами заряда. Возьмем \(q=4\text{ нКл}\) в первый раз он был при \(t=0\text{ мкс}\), а второй раз при \(t=8\text{ мкс}\), а значит период равен 8 мкс, то есть \(8 \cdot 10^{-6}\) с.
2) \(\color{red}{\small\text{Неверно }}\) Энергия катушки будет минимальная, когда энергия конденсатора будет максимальная, а это наступает при максимальном по модулю заряде (\(W=\dfrac{q^2}{2C}\)). У нас заряд по модулю максимален при \(t=0\) \(t = 4\cdot 10^{−6} c\) и \(t = 8\cdot 10^{−6} c\). Значит энергия катушки при \(t = 2\cdot 10^{−6} c\) максимальна.
3) \(\color{green}{\small\text{Верно }}\)
Энергия катушки будет минимальная, когда энергия конденсатора будет максимальная, а это наступает при максимальном по модулю заряде (\(W=\dfrac{q^2}{2C}\)). У нас заряд по модулю максимален при \(t=0\) \(t = 4\cdot 10^{−6} c\) и \(t = 8\cdot 10^{−6} c\). Значит энергия катушки при \(t = 4\cdot 10^{−6} c\) минимальна.
4) \(\color{red}{\small\text{Неверно }}\) По пункту 3) при \(t=4\cdot 10^{−6} c\) сила тока будет минимальна.
5) \(\color{red}{\small\text{Неверно }}\)
Частота \(\nu=\dfrac{1}{T}=\dfrac{1}{8\cdot 10^{-6}\text{ с}}=125\text{ кГц}\)
Демонстрационная версия ЕГЭ 2015 по физике На рис. 1 приведена схема установки, с помощью которой исследовалась зависимость напряжения на реостате от величины протекающего тока при движении ползунка реостата справа налево.

На рис. 2 приведены графики, построенные по результатам измерений для двух разных источников напряжения.
Выберите два утверждения, соответствующих результатам этих опытов.
1) При силе тока 12 А вольтметр показывает значение ЭДС источника.
2) Ток короткого замыкания равен 12 А.
3) Во втором опыте сопротивление резистора уменьшалось с большей скоростью.
4) Во втором опыте ЭДС источника в 2 раза меньше, чем в первом.
5) В первом опыте ЭДС источника равна 5 В.
1) \(\color{red}{\small\text{Неверно }}\)
Из графиков видно, что ток, равный 12 А, является током короткого замыкания, следовательно, напряжение на вольтметре будет равно 0.
2) \(\color{green}{\small\text{Верно }}\)
Верно на основе предыдущего пункта
3) \(\color{red}{\small\text{Неверно }}\)
Угол наклона первой прямой относительно координатной оси больше, следовательно, скорость изменения сопротивления выше в первом опыте
4) \(\color{green}{\small\text{Верно }}\)
На ЭДС источника указывает самая верхняя точка графика, действительно, они отличаются в два раза
5) \(\color{red}{\small\text{Неверно }}\)
В первом опыте ЭДС источника равно 10 В.



