Механика (страница 2)
Готовиться с нами - ЛЕГКО!

Два абсолютно упругих шарика подвешены на длинных нерастяжимых нитях одинаковой длины. Один из шариков массивный, а другой намного легче, чем первый. Они подвешены так, что центры шариков находятся на одной высоте и шарики касаются друг друга. Вначале отклоняют в сторону в плоскости нитей лёгкий шарик, отпускают его, и после лобового удара о тяжёлый шар лёгкий шарик отскакивает и поднимается на некоторую высоту \(h\). Затем такой же опыт проводят, отклоняя из начального положения на ту же высоту тяжёлый шар. Во сколько раз высота подъёма лёгкого шарика после удара по нему тяжёлым шаром будет отличаться от той, что была в первом случае? Потерями энергии можно пренебречь. Ответ поясните, опираясь на законы механики.
1) Высота \(h\) подъёма лёгкого шарика в первом случае, очевидно, будет равна той, на которую его подняли. Это следует из законов сохранения импульса и механической энергии при абсолютно упругом ударе о массивный шар — лёгкий шарик просто отскакивает от неподвижного тяжёлого с той же по модулю скоростью, с какой он к нему приближался, и поднимается на исходную высоту. 2) При отклонении тяжелого шарика его вся потенциальная энергия перейдет в кинетическую, и его скорость перед столкновением будет равна скорости маленького шарика 3) Запишем закон сохранения импульса и энергии \[\begin{cases}
Mv_1=MV_1+mV_2\\
\dfrac{Mv_1^2}{2}=\dfrac{MV_1^2}{2}+\dfrac{mV_2^2}{2}\\
\end{cases}\] где \(M\) и \(m\) – массы большого и маленького шариков, \(v_1\) – скорость большого шарика перед столкновением, \(V_1\) и \(V_2\) – скорости большого и маленьких шариков после столкновения. Сгруппируем слагаемые \[\begin{cases}
Mv_1-MV_1=mV_2 \\
\dfrac{Mv_1^2}{2}-\dfrac{MV_1^2}{2}=\dfrac{mV_2^2}{2}\\
\end{cases}\] Заметим разность квадратов и раскроем ее, умножив второе уравнение на 2 \[\begin{cases}
Mv_1-MV_1=mV_2 \\
M((v_1-V_1)(V_1+V_1))=mV_2^2\\
\end{cases}\] Поделим второе на первое \[V_2=v_1+V_1\] Выразим скорость большого шарика после столкновения и подставим в закон сохранения импульса \[V_1=V_2-v_1\] \[Mv_1=M(V_2-v_1)+ mV_2 \Rightarrow (M+m)V_2=2Mv_1\] Так как \[m\ll M\], то массой маленького можно пренебречь. \[V_2=2v_1\] 4) Запишем закон сохранения энергии для маленького шарика с переходом в потенциальную энергию \[\dfrac{mV_2^2}{2}=mgH \Rightarrow \dfrac{4mv_1^2}{2}=mgH\] Значит и высота увеличиться в 4 раза.
На каких колесах ехать легче: немного спущенных или полностью накаченных? Свой ответ объясните, основываясь на законах физики.
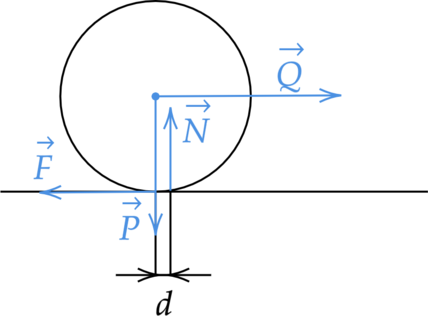
Пусть к оси катка, имеющего вес \(Р\), приложена сила \(Q\), достаточно большая для того, чтобы каток сдвинулся с места. Трение качения вызвано деформацией катящегося тела и поверхности. Сила реакции опоры \(N\) при этом смещена от вертикали, проходящей через центр колеса. Момент силы трения качения равен \[M=F\cdot d\] Если колеса велосипеда немного спущены, то деформация колеса становится больше, увеличиваются смещение \(d\) силы реакции опоры и момент силы трения качения. Поэтому ехать становится тяжелее.
Известно, что слуховой аппарат человека чувствителен к изменениям атмосферного давления — если оно быстро меняется, то уши закладывает. От этого ощущения можно избавиться, если определённым образом глотнуть воздух. Объясните, основываясь на физических законах и закономерностях, наблюдаемое явление и оцените, при спуске на лифте с какого этажа Главного здания (ГЗ) МГУ им. М.В. Ломоносова это закладывание произойдёт, если в среднем уши человека чувствуют изменение давления на 9 мм ртутного столба. Высота каждого этажа в ГЗ 5 м, а атмосферные условия близки к нормальным. Лифт опускается на первый этаж. Считайте, что в пределах высоты ГЗ плотность атмосферного воздуха не меняется.
Найдем, при какой разности давления в паскалях начинает закладывать уши \[\Delta p =\rho_{\text{рт.}}\cdot g \cdot h=13600\text{ кг/м$^3$}\cdot 10\text{ Н/кг}\cdot 0,009\text{ м} \approx 1224\text{ Па}\] Найдем также высоту поднятия, необходимую для такой же разности давления, плотность воздуха выразим из уравнения Клапейрона – Менделеева \[\rho=\dfrac{\mu p}{R T},\] где \(\mu\) – молярная масса воздуха, \(p\) – нормальное атмосферное давление, \(T\) – температура воздуха в Кельвинах.
\[\Delta p=\rho g H \Rightarrow H =\dfrac{\Delta p}{\rho g}=\dfrac{1224\text{ Па}}{\dfrac{29 \cdot 10^{-3}\text{ кг/моль}\cdot 10^5 \text{ Па}}{8,31\text{ Дж/(моль $\cdot$ К)} \cdot 273 \text{ К}}}\approx 96\text{ м}\] Найдем количество этажей \[n=\dfrac{H}{5}\approx 10\]
Колесо катится по горизонтальной плоскости без проскальзывания, внутри колеса лежит небольшое тело массой \(m\). Основываясь на законах физики, объясните, в какой точке колеса давление на колесо со стороны тела будет максимальным? сделайте схематичный рисунок с указанием всех сил, действующих на тело.

Введем ось \(Oy\), направленную в центр колеса, тогда сила реакции опоры в проекции на ось \(Oy\) равна \(mg\cos \alpha\). Из курса физики давление на колесо будет по модулю равно силе реакции опоры колеса, следовательно, чтобы сила реакции опоры была максимальна, косинус угла должен быть максимален, что достигается в нижней точке \(\cos \alpha =1\) и тогда давление на колесо будет равно \(mg\).
Тело бросили два раза под углами \(\alpha\) и \(90-\alpha\) к горизонту. Найдите отношение дальностей полета тела в первом и во втором случае. Ответ дайте, основываясь на законах физики. Нарисуйте схематично траекторию движения тела в обоих случаях.
Выведем формулу дальности полета тела.
Время подъема тела на максимальную высоту (снижение до земли с максимальной высоты) равно \[0=v_0\sin \alpha -gt \Rightarrow t=\dfrac{v_0\sin \alpha}{g}\] Откуда время всего полета тела \[\tau=2t=\dfrac{2v_0 \sin \alpha}{g}\quad (1)\] Дальность полета тела выражена формулой \[L=v_0\cos \alpha t \quad (2)\] Объединим (1) и (2) и получим \[L=\dfrac{2 \cdot v_0^2 \sin \alpha \cos \alpha}{g}=\dfrac{v_0^2 \sin 2\alpha}{g}\] Подставим наши углы \(\alpha\) и \(90-\alpha\) \[L_{\alpha}= \dfrac{v_0^2 \sin 2\alpha}{g}\] \[L_{90-\alpha}=\dfrac{v_0^2 \sin (180-2\alpha)}{g}= \dfrac{v_0^2 \sin 2\alpha}{g}\] Получились две одинаковые формулы, следовательно, дальности полетов одинаковые. Нарисуем траектории движения 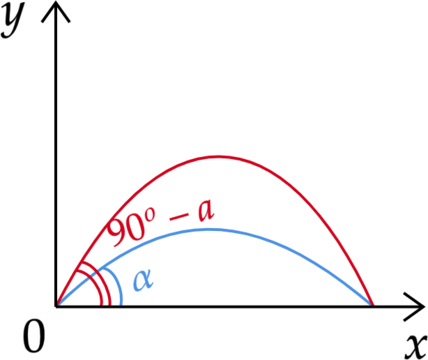
Будет ли разница в действии гидравлического пресса на земле и на луне
Гидравлический пресс состоит из сосуда с жидкостью и двух плеч площадью \(S_1\) и \(S_2\), причем \(S_2\) << \(S_1\). А формула для пресса \[\dfrac{F_1}{S_1} =\dfrac{F_2}{S_2} \Rightarrow \dfrac{F_2}{F_1}=\dfrac{S_2}{S_1}\] Так как площади остаются неизменными, то и силы остаются неизменными, Значит, разницы нет.


