Волновая оптика (страница 2)

Интерференция — такое наложение волн, при котором происходит их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от соотношения между фазами этих волн.

Необходимые условия для наблюдения интерференции:

1) Волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени;

2) Волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции. Волны, для которых выполняются эти два условия, называются когерентными.

При наложении когерентных волн возможны два предельных случая:

1) Условие максимума:

Разность хода волн равна целому числу длин волн (иначе четному числу длин полуволн). \[d_2=d_1=2k\dfrac{\lambda}{2}\] где (\(k=0, \pm 1,\pm 2, \pm 3...\)). В этом случае волны в рассматриваемой точке приходят с одинаковыми фазами и усиливают друг друга –– амплитуда колебаний этой точки максимальна и равна удвоенной амплитуде.

2) Условие минимума:

Разность хода волн равна нечетному числу длин полуволн. \[d_2=d_1=(2k+1)\dfrac{\lambda}{2}\] где (\(k=0, \pm 1,\pm 2, \pm 3...\)). Волны приходят в рассматриваемую точку в противофазе и гасят друг друга. Амплитуда колебаний данной точки равна нулю.

Принцип Гюйгенса

Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.

Дифракция волн — явление отклонения волны от прямолинейного распространения и огибания волной препятствия.

При дифракции происходит искривление поверхности волны у краев препятствия. Особенно явно дифракция проявляется в том случае, если размеры препятствия сравнимы с длинами волн.

Явление дифракции можно объяснить при помощи принципа Гюйгенса, так как любую точку поля волны следует рассматривать как источник вторичных волн, которые распространяются по всем направлениям, в том числе и в область геометрической тени препятствия.

В прозрачной плоской дифракционной решетке (см. рисунок) ширина прозрачного штриха равна \(a\), ширина непрозрачного промежутка — \(b\). Величина \(d=a+b=\dfrac{1}{N}\) называется периодом дифракционной решетки, где \(N\) — число штрихов на единицу длины решетки.

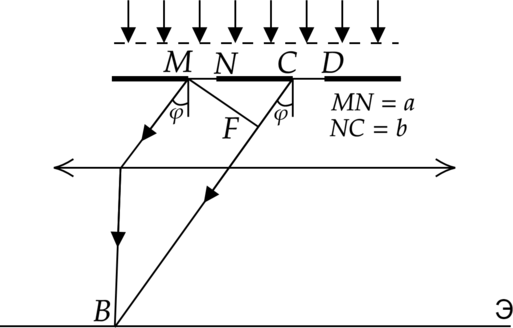
Пусть плоская монохроматическая волна падает нормально к плоскости решетки. По принципу Гюйгенса-Френеля каждая щель является источником вторичных волн, способных интерферировать друг с другом. Получившуюся дифракционную картину можно наблюдать в фокальной плоскости линзы, на которую падает дифрагированный пучок.

Допустим, что свет дифрагирует на щелях под углом \(\varphi\). Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, для данного направления \(\varphi\) будут одинаковыми в пределах всей дифракционной решетки:

\[\Delta=CF=(a+b)\sin\varphi=d\sin\varphi\]

В тех направлениях, для которых разность хода равна четному числу полуволн, наблюдается интерференционный максимум. Наоборот, для тех направлений, где разность хода равна нечетному числу полуволн, наблюдается интерференционный минимум. Таким образом, в направлениях, для которых углы \(\varphi\) удовлетворяют условию

\[d\sin\varphi=m\lambda, (m=0,1,2,...)\]

наблюдаются главные максимумы дифракционной картины. Эту формулу называют формулой дифракционной решетки. В ней \(m\) называется порядком главного максимума. Между главными максимумами располагается \((N - 2)\) слабых побочных максимумов, но на фоне ярких главных максимумов они практически не видны. При увеличении числа штрихов \(N\) главные максимумы, оставаясь на прежних местах, становятся более резкими.

При наблюдении дифракции в белом свете все главные максимумы, кроме нулевого центрального максимума, окрашены. Это объясняется тем, что, как видно из формулы \[\sin\varphi=\dfrac{m\lambda}{d}\] различным длинам волн соответствуют различные углы, на которых наблюдаются интерференционные максимумы.

Звуковыми волнами в широком смысле называются всякие волны, распространяющиеся в упругой среде. В узком смысле звуком называют звуковые волны в диапазоне частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом. Ниже этого диапазона лежит область инфразвука, выше — область ультразвука.

К основным характеристикам звука относятся громкость и высота. Громкость звука определяется амплитудой колебаний давления в звуковой волнеиизмеряется в специальных единицах — децибелах (дБ). Чем больше амплитуда колебаний в звуковой волне, тем громче звук.

Скорость звука в разных средах различна: чем более упругой является среда, тем быстрее в ней распространяется звук. В жидкостях скорость звука больше, чем в газах, а в твёрдых телах — больше, чем в жидкостях.