Колебательный контур
Готовиться с нами - ЛЕГКО!

На рисунке приведен график гармонических колебаний тока в колебательном контуре. 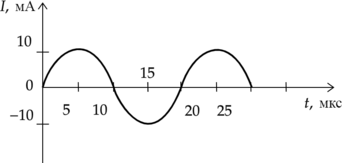
Если катушку в этом контуре заменили на другую катушку, индуктивность которой в 9 раз больше. Чему равен период колебаний? (Ответ дать в мкс.)
Из графика видно, что период колебаний равен \[T=20 \text{ мкс}\].
Период колебаний электромагнитного контура вычисляется по формуле Томсона: \[T=2\pi\sqrt{LC}\] Если катушку заменить на другую катушку, индуктивность которой в 9 раз больше, то период увеличится в 3 раза, следовательно, станет равным 60 мкс.
В наборе радиодеталей для изготовления простого колебательного контура имеются две катушки с индуктивностями \(L_1=1\) мкГн и \(L_2=2\) мкГн, а также два конденсатора, ёмкости которых \(C_1=30\) пФ и \(C_2=40\) пФ. С какой наименьшей собственной частотой \(\nu\) можно составить колебательный контур из двух элементов этого набора? (Ответ выразите в МГц и округлите до целого числа.)
Период колебаний электромагнитного контура вычисляется по формуле Томсона: \[T=2\pi\sqrt{LC}\] Чтобы частота была наименьшей, период должен быть наибольшим Значит надо взять катушку с индуктивностью \(L_2=2\) мкГн, конденсатор \(C_2=40\) пФ.
Найдем частоту: \[\nu=\frac{1}{2\pi\sqrt{LC}}=\frac{1}{2\cdot3,14\cdot\sqrt{2\cdot10^{-6}\text{ Гн}\cdot40\cdot10^{-12}}\text{ Ф}}=18\text{ МГц}\]
Во сколько раз уменьшится частота собственных колебаний контура, если его индуктивность увеличить в 10 раз, а емкость уменьшить в 2,5 раза?
Период колебаний электромагнитного контура вычисляется по формуле Томсона: \[T=2\pi\sqrt{LC},\] где \(L\) – индуктивность катушки, \(C\) – ёмкость конденсатора. Частота: \[\nu=\frac{1}{2\pi\sqrt{LC}}\] Если индуктивность увеличить в 10 раз, а емкость уменьшить в 2,5 раза, то корень увеличится в 4 раза, следовательно, частота уменьшится в 2 раза
Колебательный контур с конденсатором емкостью 1 мкФ настроен на частоту 400 Гц. Если подключить к нему параллельно второй конденсатор, то частота колебаний в контуре становится равной 200 Гц. Определите емкость (в мкФ) второго конденсатора.
Период колебаний электромагнитного контура вычисляется по формуле Томсона: \[T=2\pi\sqrt{LC},\] где \(L\) – индуктивность катушки, \(C\) – ёмкость конденсатора. Частота: \[\nu=\frac{1}{2\pi\sqrt{LC}}\] Частота уменьшилась в 2 раза, следовательно, емкость батареи конденсаторов в 4 раза больше изначальной. При параллельном соединении конденсаторов общая ёмкость равна \[C_{\text{общ}}=C_2+C_1=4C_1 \text{ мкФ}\] \[C_2=3C_1=3 \text{ мкФ}\]
В колебательном контуре к конденсатору параллельно присоединили другой конденсатор, втрое большей емкости, после чего частота колебаний контура уменьшилась на 300 Гц. Найдите первоначальную частоту колебаний контура.
Период колебаний электромагнитного контура вычисляется по формуле Томсона: \[T=2\pi\sqrt{LC},\] где \(L\) – индуктивность катушки, \(C\) – ёмкость конденсатора. Частота: \[\nu=\frac{1}{2\pi\sqrt{LC}}\] \[\frac{\nu_0-\Delta \nu}{\nu_0}=\sqrt{\frac{C_0}{C_0+3C_0}}\] \[2(\nu_0-\Delta \nu)=\nu_0\] \[\nu_0=2\Delta \nu=600 \text{ Гц}\]
Колебательный контур состоит из катушки и конденсатора. Во сколько раз увеличится частота собственных колебаний в контуре, если в контур последовательно включить второй конденсатор, емкость которого в 3 раза меньше емкости первого?
Период колебаний электромагнитного контура вычисляется по формуле Томсона: \[T=2\pi\sqrt{LC},\] где \(L\) – индуктивность катушки, \(C\) – ёмкость конденсатора. Частота: \[\nu=\frac{1}{2\pi\sqrt{LC}}\] При последовательном соединении конденсаторов: \[\frac{1}{C_{\text{общ}}}=\frac{1}{C_1}+\frac{3}{C_1}\] \[C_{\text{общ}}=\frac{C_1}{4}\] Емкость уменьшилась в 4 раза, следовательно, частота увеличилась в 2 раза.
На какую длину волны настроен радиоприемник, если его колебательный контур обладает индуктивностью 3 мГн и емкостью 3 нФ?
Период колебаний электромагнитного контура вычисляется по формуле Томсона: \[T=2\pi\sqrt{LC}\] Длина волны: \[\lambda=cT=3\cdot10^8\cdot2\cdot \pi \sqrt{3\cdot10^{-3}\cdot3\cdot10^{-9}}=5652\text{ м}\]



