Кинематика (страница 3)
Готовиться с нами - ЛЕГКО!

Тело бросили под углом к горизонту из начала системы координат. В таблице приведены результаты измерения координат тела в зависимости от времени. Выберите два верных утверждения на основании данных, приведенных в таблице. Силами сопротивления пренебречь.
\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline \text{Время, с} & 0,2 & 0,4 & 0,6 & 0,8 & 1 & 1,2 & 1,4 & 1,6\\ \hline \text{Координата x, м} & 0,4 & 0,8 & 1,2 & 1,6 & 2 & 2,4 & 2,8 & 3,2\\ \hline \text{Координата y, м} & 0,7 & 1,2 & 1,5 & 1,6 & 1,5 & 1,2 & 0,7 & 0\\ \hline \end{array}\]
1) Максимальная высота полета тела равна 3,2 м.
2) Полная механическая энергия тела уменьшилась за первые 0,8 секунды.
3) Тело бросили со скоростью 6 м/с.
4) В момент времени 0,8 с скорость движения тела равна 2 м/с.
5) Тело движется равноускоренно по обоим осям.
1) \(\color{red}{\small \text{Неверно}}\)
Максимальная высота полета равна максимальной координате y, которая равна 1,6 м.
2) \(\color{red}{\small \text{Неверно}}\)
Полная механическая энергия тела не изменяется, так как нет никаких сил сопротивления.
3) \(\color{green}{\small \text{Верно}}\)
По данным таблицы видно, что по оси \(Ox\) тело движется равномерно, за 1 с тело проходит по оси \(Ox\) 2 м, следовательно \(v_{x}=2\) м/с. В верхней точке траектории \(v_{y}=0\) м/с. По закону сохранения энергии \[E_{k1}+E_{p1}=E_{k2}\] 1 – в вершине траектории, 2 – в момент броска. \[\frac{mv^{2}_{x}}{2}+mgh=\frac{mv^{2}}{2}\Rightarrow v^{2}=2gh+v^{2}_{x}\Rightarrow v^{2}=2\cdot10\cdot1,6+2^{2}=36\Rightarrow v=6 \text{ м/с }\]
4) \(\color{green}{\small \text{Верно}}\)
По данным таблицы видно, что по оси \(Ox\) тело движется равномерно, за 1 с тело проходит по оси \(Ox\) 2 м, следовательно \(v_{x}=2\) м/с. В верхней точке траектории \(v_{y}=0\) м/с. То есть в верхней точке траектории скорость тела равна скорости тела по оси \(Ox\), равна 2 м/с.
5) \(\color{red}{\small \text{Неверно}}\)
По данным таблицы видно, что по оси \(Ox\) тело движется равномерно, а по оси \(Oy\) с постоянным ускорением \(g\).
На рисунке изображены графики зависимости координаты от времени для двух тел: A и В. Они движутся только по одной прямой, вдоль которой направлена ось \(Ox\). Выберите два верных утверждения о характере движения тел:
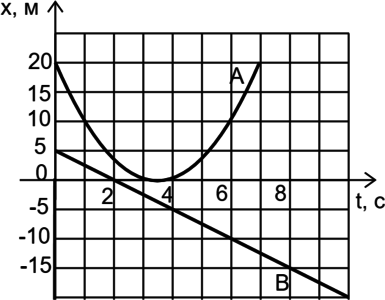
1) Тело В имеет постоянное ускорение.
2) Тело А имеет переменное ускорение.
3) В момент времени \(t=2\text{ с}\) тело В движется со скоростью \(-2,5\) м/с.
4) За интервал времени от 1 с до 7 с тело А прошло путь, равный 10 м.
5) Тело А имеет максимальную по модулю скорости в моменты времени \(t_1=0\) и \(t_2=7\text{ с}\).
1) \(\color{red}{\small \text{Неверно}}\)
График В – прямая, следовательно тело В движется равномерно, без ускорения.
2) \(\color{red}{\small \text{Неверно}}\)
График А – парабола, следовательно тело А движется равноускоренно, ускорение не меняется.
3) \(\color{green}{\small \text{Верно}}\)
График В – прямая, следовательно скорость одинакова на всем пути, можно заметить, что за 2 с тело В прошло 5 м против оси \(Ox\), т. е. за 1 с – 2,5 м, следовательно скорость тела В равна -2,5 м/с.
4) \(\color{red}{\small \text{Неверно}}\)
Не путаем перемещение и путь! Тело А переместилось на 10 м (20 м - 10 м = 10 м) и прошло 30 м (10 м + 20 м).
5) \(\color{green}{\small \text{Верно}}\)
Скорость – это производная пути. График А имеет максимальные по модулю производные в моменты времени \(t=0;7\text{ с}\).
На рисунке приведен график зависимости координаты от времени для тела, движущегося вдоль оси \(Ox\) без начальной скорости. Масса тела равна 1,5 кг. Выберите два верных утверждения, описывающих характер движения тела:
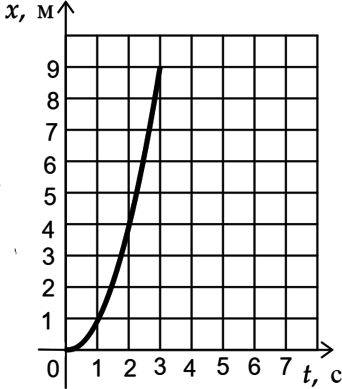
1) Тело движется равномерно.
2) Скорость тела в момент времени \(t=2\text{ с}\) равна 4 м/с
3) За промежуток времени от 2 с до 3 с кинетическая энергия тела увеличилась в 2,5 раза.
4) За первые 2 секунды суммарная работа всех сил, действующих на тело, равна 12 Дж.
5) Равнодействующая всех сил, действующих на тело, постоянно возростала.
1) \(\color{red}{\small \text{Неверно}}\)
График – парабола, значит тело движется равноускоренно.
2) \(\color{green}{\small \text{Верно}}\)
Нетрудно заметить, что \(x=t^{2}\), а кинематическое уравнение выглядит так: \[x(t)=\frac{at^{2}}{2}\] Следовательно только при \(a=2\text{ м/с}^{2}\) выполняется равенство \(x=t^{2}\), значит \(a=2\text{ м/с}^{2}\).
Скорость находится по формуле: \[v(t)=at\Rightarrow v(2)=2\cdot2=4\text{ м/с}\]
3) \(\color{red}{\small \text{Неверно}}\)
Кинетическая энергия находится по формуле: \[E_{k}=\frac{mv^{2}}{2}\] \[E_{k2}=\frac{mv^{2}_{2}}{2}\] \[E_{k3}=\frac{mv_{3}^{2}}{2}\]
\(E_{k2}\) – кинетическая энергия тела в момент времени 2 с, \(E_{k3}\) – кинетическая энергия тела в момент времени 3 с, \(v_{2}=4\text{ м/с}\) (из решения 2 утверждения), \(v_{3}=6\text{ м/с}\) (нашли также как \(v_{2}\)), тогда \[\frac{E_{k3}}{E_{k2}}=\frac{v_{3}^{2}}{v^{2}_{2}}=\frac{36}{16}=2,25\]
4) \(\color{green}{\small \text{Верно}}\)
Работа в данном случае вычисляется по формуле: \[A=FS\] где \(F\) – равнодействующая всех сил, действующих на тело, \(S\) – путь, пройденный телом за 2 с. \[F=ma\Rightarrow A=maS=1,5\cdot2\cdot4=12\text{ Дж}\]
5) \(\color{red}{\small \text{Неверно}}\)
Равнодействующая всех сил, действующих на тело, вычисляется по формуле: \[F=ma\]
То есть равнодействующая всех сил, действующих на тело, прямо пропорциональна ускорению, следовательно так как ускорение не изменяется, то не изменяется и равнодействующая всех сил, действующих на тело.
На рисунке представлен график зависимости скорости от времени для тела, движущегося по оси \(Ox\). Выберите два верных утверждения, описываюших движение тела.
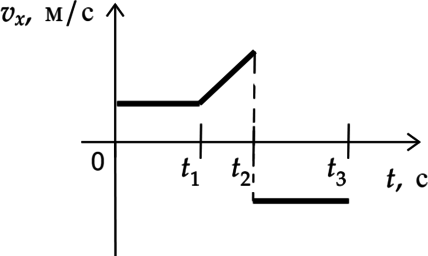
1) В интервале времени от 0 до \(t_{1}\) тело движется равномерно.
2) Тело все время движется в одном направлении.
3) В интервале времени от \(t_{2}\) до \(t_{3}\) тело покоится.
4) В интервале от \(t_{1}\) до \(t_{2}\) тело движется равноускоренно.
5) В интервале времени от 0 до \(t_{1}\) кинетическая энергия тела увеличивается.
1) \(\color{green}{\small \text{Верно}}\)
По графику видно, что в данный интервал времени скорость больше 0 и не изменяется, занчит тело движется равномерно.
2) \(\color{red}{\small \text{Неверно}}\)
В момент времени \(t_{2}\) скорость меняет знак, значит тело начинает двигаться в обратном направлении.
3) \(\color{red}{\small \text{Неверно}}\)
По графику видно, что в данный интервал скорость не равна 0, значит тело движется.
4) \(\color{green}{\small \text{Верно}}\)
График в данном интервале является прямой, не параллельной оси \(Ot\). Значит тело имеет постоянное ускорение.
5) \(\color{red}{\small \text{Неверно}}\)
По графику видно, что в данном интервале скорость постоянна, а кинетическая энергия прямо пропорциональна скорости, следовательно кинетическая энергия не изменяется.
Тело бросили под углом \(45^{\circ}\) к горизонту со скоростью 8\(\sqrt{2}\) м/с. Сопротивление воздуха не учитывать. Выберите два верных утверждения, описывающих движение тела.
1) Скорость тела на максимальной высоте траектории равна нулю.
2) Максимальная высота полета равна 3,5 м.
3) Тело находилось в воздухе 1,6 с.
4) Потенциальная энергия монотонно увеличивается за все время полета.
5) Дальность полета примерно равна 12,8 м
1) \(\color{red}{\small \text{Неверно}}\)
Введем систему координат: по вертикали – ось \(Oy\), по горизонтали – ось \(Ox\). На тело не действуют никакие силы на оси \(Ox\), поэтому горизонтальная скорость остается неизменной, следовательно скорость тела на максимальной высоте траектории равна начальной горизонтальной скорости.
2) \(\color{red}{\small \text{Неверно}}\)
Найдем проекции скорости на оси \(Ox\) и \(Oy\) из теругольника скоростей:
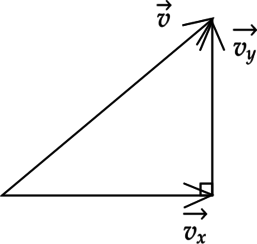
Так как у нас угол между скоростью и горизонтом \(45^{\circ}\), то треугольник равнобедренный и \(v_{0x}=v_{0y}\). По теореме пифагора: \[v^{2}=v_{0x}^{2}+v_{0y}^{2}\Rightarrow v_{0x}=v_{0y}=8 \text{ м/с}\]
Рассмотрим начальное положение и положение тела в верхней точке:
По закону сохранения энергии: \[E_{k}=E_{k1}+E_{p1}\Rightarrow v^{2}=v_{0x}^{2}+2gh\Rightarrow h=\frac{v^{2}-v_{0x}^{2}}{2g}=\frac{128-64}{20}=3,2\text{ м}\]
3) \(\color{green}{\small \text{Верно}}\)
Запишем кинематическое уравнение для оси \(Oy\): \[y(t)=v_{0y}t-\frac{gt^{2}}{2}\] Тело пролетело путь и упало, то есть когда пройдет время полета, координата \(y\) будет равняться 0.
\[0=v_{0y}t-\frac{gt^{2}}{2}\Rightarrow t=\frac{2v_{0y}}{g}=\frac{2\cdot8}{10}=1,6\text{ с}\]
4) \(\color{red}{\small \text{Неверно}}\)
Потенциальная энергия вначале увеличивается до достижения телом вершины траектории, после потенциальная энергия уменьшается
5) \(\color{green}{\small \text{Верно}}\)
Дальность полёта можно найти по формуле: \[x=v_{0x}t\] где \(t\) – время полета, \(x\) – дальность полетаю.
\[x=8\cdot1,6=12,8\text{ м}\]
В инерциальной системе отчета вдоль оси \(Ox\) движется тело массой 10 кг. На рисунке приведен график зависимости проекции скорости \(v_{x}\) этого тела от времени \(t\). Выберите два верных утверждения, описывающих движение тела:
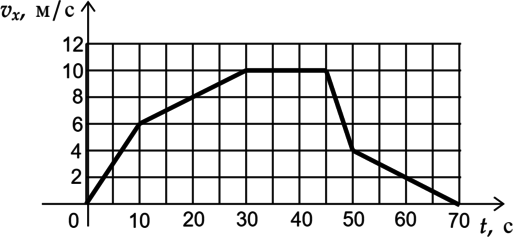
1) Кинетическая энергия тела в промежутке от 10 с до 30 с увеличилась на 450 Дж.
2) Модуль ускорения тела в промежутке времени от 45 с до 50 в 5 раз больше модуля ускорения тела в промежутке времени от 10 с до 30 с.
3) В промежутке времени от 0 с до 30 с тело переместилось на 200 м.
4) За промежуток времени от 45 с до 50 с импульс тела уменьшился на 60 кг\(\cdot\)м/с.
5) В момент времени \(t=15\text{ с}\) равнодействующая всех сил, действующих на тело, равна 2 Н.
1) \(\color{red}{\small \text{Неверно}}\)
Кинетическая энергия вычисляется по формуле: \[E_{k}=\frac{mv^{2}}{2}\] Начальная и конечная кинетические энергии равны: \[E_{k1}=\frac{10\cdot6^{2}}{2}=180\text{ Дж }\] \[E_{k2}=\frac{10\cdot10^{2}}{2}=500\text{ Дж }\] \[E_{k2}-E_{k1}=500-180=320\text{ Дж }\] То есть кинетическая энергия тела увеличилась на 320 Дж.
2) \(\color{red}{\small \text{Неверно}}\)
Ускорение вычисляется по формуле: \[a=\frac{\Delta v}{\Delta t}\] \[\vert a_{1} \vert=\frac{10-4}{5}=1,2 \text{ м/с}^2\] \[\vert a_{2} \vert=\frac{10-6}{20}=0,2\text{ м/с}^2\] \[\frac{\vert a_{1}\vert}{\vert a_{2}\vert}=\frac{1,2}{0,2}=6\] То есть Модуль ускорения тела в промежутке времени от 45 с до 50 в 6 раз больше модуля ускорения тела в промежутке времени от 10 с до 30 с.
3) \(\color{red}{\small \text{Неверно}}\)
В данном графике перемещение – это площадь под графиком.
Площадь треугольника равна \[S_1=\frac{10\cdot6}{2}=30 \text{ м }\]
Площадь трапеции равна \[S_2=\frac{(6+10)\cdot20}{2}=160\text{ м }\] Тогда перемещение за промежуток времени от 0 до 30 с равно \(S=S_1+S_2=30\text{ м }+160\text{ м }=190 \text{ м }\).
4) \(\color{green}{\small \text{Верно}}\)
Импульс тела вычисляется по формуле:\[p=mv\] \[p_{1}=10\cdot10=100\text{ кг$\cdot$м/с}\] \[p_{2}=4\cdot10=40\text{ кг$\cdot$м/с}\] \[p_{2}-p_{1}=40-100=-60\text{ кг$\cdot$м/с}\] То есть за промежуток времени от 45 с до 50 с импульс тела уменьшился на 60 кг\(\cdot\)м/с.
5) \(\color{green}{\small \text{Верно}}\)
Равнодействующая всех сил вычисляется по формуле: \[F=ma\] Ускорение в этот момент времени равно: \[a=\frac{10-6}{20}=0,2\text{ м/с$^{2}$}\Rightarrow F=10\cdot0,2=2\text{ Н }\]
На рисунке изображен график зависимости координаты от времени для тела. Оно движется только по одной прямой, вдоль которой направлена ось \(Ox\). Выберите два верных утверждения о характере движения тела:
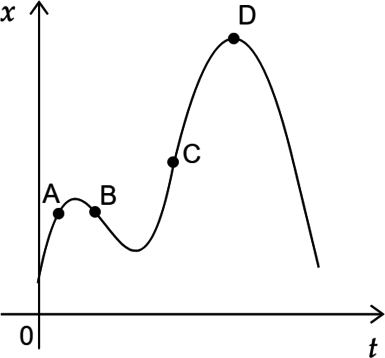
1) Проекция перемещения тела на ось \(Ox\) при переходе из точки A в точку D отрицательна.
2) Скорость тела в точке D равна нулю.
3) В точке В проекция скорости тела на ось \(Ox\) положительна.
4) На участке CD модуль скорости монотонно уменьшается.
5) Ускорение тела в точке D равно нулю.
1) \(\color{red}{\small \text{Неверно}}\)
Точка D по оси \(Ox\) выше точки A, следовательно проекция перемещения положитеьна.
2) \(\color{green}{\small \text{Верно}}\)
Скорость – это производная от перемещения тела, следовательно, значение скорости в той или иной точке равно угловому коэффициенту касательных, проведенных в них. Производная в точке D равна нулю, следовательно скорость в этой точке тоже равна нулю (тело меняет направление движения).
3) \(\color{red}{\small \text{Неверно}}\)
В точке В график убывает \(\Rightarrow\) производная отрицательна \(\Rightarrow\) проекция скорость на ось \(Ox\) отрицательна.
4) \(\color{green}{\small \text{Верно}}\)
Угол между касательной к графику и осью \(Ot\) постоянно уменьшается на участке СD \(\Rightarrow\) уменьшается производная \(\Rightarrow\) уменьшается скорость.
5) \(\color{red}{\small \text{Неверно}}\)
Скорость тела в точке D равна нулю, тогда если у тела в точке D нет ускорения, то тело должно остановиться, но оно продолжает движение \(\Rightarrow\) есть ускорение.



