Кинематика (страница 4)
Готовиться с нами - ЛЕГКО!

Четыре байкера движутся по прямому шоссе с одинаковыми скоростями \(\upsilon\), 1 и 2 – на концерт (в одном направлении (вдоль оси \(Ox\))), а 3 и 4 – им навстречу с концерта. Определите проекции их относительных скоростей на ось \(Ox\).
\[\begin{array}{cc}
\text{А) 2 относительно 1 }& \text{ 1) $\upsilon$ }\\
\text{Б) 1 относительно 3 }& \text{ 2) $2\upsilon$ }\\
& \text{ 3)$-\upsilon$ }\\
& \text{ 4)$-2\upsilon$ }\\
&\text{ 5) 0}\\
\end{array}\]
Запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{|c|c|}
\hline
\text{ A }&\text{ Б }\\
\hline
&\\
\hline
\end{array}\]
Проекция на ось \(Ox\) скорости любого байкера из первой пары относительно любого из второй пары: \[\upsilon_{\text{отн1}}' = \upsilon - ( -\upsilon) = 2\upsilon\]
И наоборот, проекция относительной скорости любого байкера из второй пары в системе отсчёта первой: \[\upsilon_{\text{отн2}}' = -\upsilon -\upsilon = -2\upsilon\]
Внутри каждой из пары байкеры покоятся друг относительно друга, т.е. для них относительная скорость равна нулю.
Тело первую половину пути проходит со скоростью \(\upsilon_{1}\), а вторую – со скоростью \(\upsilon_{2}\). Как изменится средняя скорость на всём пути, если
\[\begin{array}{cc}
\text{А) увеличить весь путь в 2 раза, }& \text{ 1) увеличится в 2 раза }\\
\text{Б) увеличить каждую из скоростей в 2 раза, }& \text{ 2) увеличится в 4 раза }\\
& \text{ 3) уменьшится в 2 раза }\\ & \text{ 4) уменьшится в 4 раза } \\
&\text{ 5) не изменится}\\
\end{array}\]
Запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{|c|c|}
\hline
\text{ A }&\text{ Б }\\
\hline
&\\
\hline
\end{array}\]
Средняя скорость на всём пути: \[\displaystyle \upsilon_{\text{ ср}} = \frac{S_{1} + S_{2}}{t_{1 } + t_{2}}.\]
Пусть весь путь \(S = 2l\), тогда \(S_{1} = l\), \(S_{2} = l\), \(t_{1} = \dfrac{l}{\upsilon_{1}}\), \( t_{2} = \dfrac{l}{\upsilon_{2}}\).
Отсюда \[\displaystyle \upsilon_{\text{ ср}} = \dfrac{2l}{\dfrac{l}{\upsilon_{1}} + \dfrac{l}{\upsilon_{2}}} = \dfrac{2\upsilon_{1}\upsilon_{2}}{\upsilon_{1} + \upsilon_{2}}.\]
Значит средняя скорость зависит только от скоростей \(\upsilon_{1}\) и \(\upsilon_{2}\) на каждой из половин пути и не зависит от длины самого пути, поэтому вопросу А соответствует 5.
В других случаях, поскольку \(\upsilon_{1}\) и \(\upsilon_{2}\) изменяются в одинаковое число раз, средняя скорость изменяется пропорционально изменению одной из скоростей \(\Rightarrow\) Б = 1
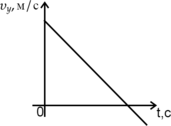
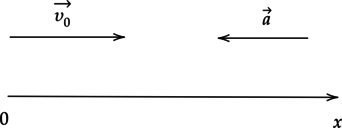
Тело движется вдоль оси \(Ox\) из начала координат с постоянным ускорением. Направления начальной скорости и ускорения \(a\) тела указаны на рисунке.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные под соответствующими буквами. \[\begin{array}{cc} \text{ Физические величины}&\text{ Формулы}\\ \text{А) Координата x тела в момент времени t;}& \text{ 1) } \displaystyle v_0t+\frac{at^2}{2} \\ \text{Б) Скорость $v_x$ тела в момент времени t.}& \text{ 2) } \displaystyle v_0t - \frac{at^2}{2}\\ & \text{ 3) } \displaystyle v_0 - at\\ &\text{ 4) } \displaystyle v_0 +at\\ \end{array}\]
\[\begin{array}{|c|c|} \hline \text{ A }&\text{ Б }\\ \hline &\\ \hline \end{array}\]
Проекция вектора ускорения \(\vec{a}\) на ось \(Ox\): \(a_x=-a\). Проекция вектора начальной скорости \(\vec{\upsilon_{0}}\) на ось \(Ox\): \(v_x=v_0\). Так как тело начинает движение из начала координат, координата тела \(x\) в момент времени \(t\): \[x=\upsilon_{0}t - \dfrac{at^{2}}{2}\]
(А — 2)
Скорость \(\upsilon_{x}\) тела в момент времени t: \[v_x=v_0 - at\]
(Б — 3)
Мальчик кинул мячик так, что координата мячика по оси \(Oy\) с течением вемени \(t\) менялась по закону: \(y= 9+10t - 5t^2\) (все величины выражены в СИ).
Установите соответстивие между графиками зависимости и величинами, зависимости которых от времени \(t\) они могут изображать. К каждой позиции первого столбца подберите соответствующую позицию из второго. В ответ укажите последовательность цифр.
ГРАФИКИ: 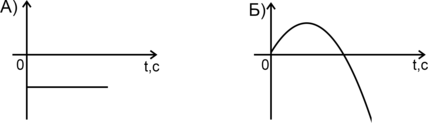
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ:
1) Проекция перемещения тела, \(S_y\)
2) Модуль ранодействующей всех сил, \(R\)
3) Проекция ускорения, \(a_y\)
4) Проекция скорорости тела, \(\upsilon_y\)
\[\begin{array}{|c|c|} \hline \text{A}&\text{Б}\\ \hline &\\ \hline \end{array}\]
1) Основное уравнение кинематики \[y=y_0 +\upsilon_y\cdot t+\frac{a_yt^2}{2}\] где \(y_0\) — начальная координата, \(\upsilon_y\)— проекция скорости на \(Ox\), \(a_y\) — проекция ускорения на \(Ox\).
2) Перемещение тела можно найти как разность начальной и конечной координат мячика: \[S=y-9 = 10t - 5t^2\] Так как это квадратное уравнение относительно переменной t, то его график — парабола, у которой ветви вниз, ведь перед \(t^2\) стоит минус. При чём в момент времени \(t=0\) координата по оси \(Oy\) равна нулю. Это соответствует графику Б \(\Rightarrow\) Б — 1.
3) Из уравнения видно, что проекция ускорения \(a_y = -10\) м/с\(^2\) \(\Rightarrow\) график её зависимости от времени \(t\) — прямая, проходящая ниже нуля и параллельная \(Oy\). Этому соответсвует график А \(\Rightarrow\) А — 3.
4) Модуль равнодействующих всех сил равен: \[|R| = |ma| = const > 0\]
Значит, график зависмости равнодействующей \(R\) от времени \(t\) будет выглядеть так: 
5) Так как скорость — это производная координаты по времени, то: \[\upsilon_y = y' = 10-10t\]
Значит, график зависимости проекции скорости на \(Oy\) от времени будет выглядеть так: