Законы сохранения в механике
Готовиться с нами - ЛЕГКО!

Брусок съезжает без трения с горки высотой \(H\). Начальная скорость равна нулю, ускорение свободного падения равно \(g\). У подножья модуль испульса был равен \(p\). Определите массу бруска и кинетическую энергию у подножья горки.
Установите соответствие между физическими величинами и формулами, по которымих можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго столбца.
\[\begin{array}{cccccccc}
\text{ Физические величины}& & & & & & &\text{ Формулы}\\\\
\text{А) Масса бруска}& & & & & & & \text{ 1) } \displaystyle \frac{p\sqrt{gH}}{\sqrt{2}} \\\\ & & & & & & & \text{ 2) } \displaystyle \frac{2gH}{\sqrt{p}}\\\\
\text{Б) Кинетическая энергия бруска у подножья }& & & & & & & \text{ 3) } \displaystyle \frac{p}{\sqrt{2gH}}\\\\
& & & & & & &\text{ 4) } \displaystyle \frac{2\sqrt{p}}{gH}\\
\end{array}\] \[\begin{array}{|c|c|}
\hline
\text{А}&\text{Б}\\
\hline
&\\
\hline
\end{array}\]
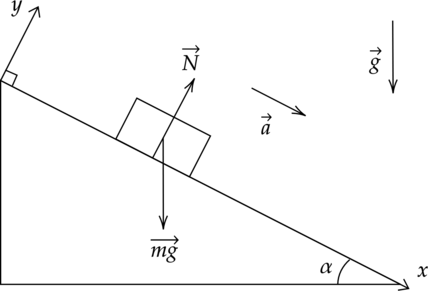
A) Так как трение отсутствует, то вся энергия переходит из одного состояния в другое: \[E_\text{пот}=E_\text{кин}\] \[mgH=\frac{m\upsilon^2}{2}=\frac{m^2\upsilon^2}{2m}\] Знаем, что \(p=m\upsilon\), тогда преобразуем формулу в следующем виде: \[mgH=\frac{p^2}{2m}\] \[m^2=\frac{p^2}{2gH}\] \[m=\frac{p}{\sqrt{2gH}}\] A — 3
Б) Энергия: \[E_\text{кин}=E_\text{пот}\] \[E_\text{кин}=mgH=\frac{p}{\sqrt{2gH}}\cdot gH=\frac{p\sqrt{gH}}{\sqrt{2}}\] Б — 1
Тело массой \(m=20\) кг движется по прямой с ускорением \(a=1\) м/с\(^2\). Под действием силы трения \(F_\text{тр}\) импульс тела уменьшился от 200 кг\(\cdot\)м/с до 120 кг\(\cdot\)м/с. Найдите коэффициент трения и время, за которое это произошло.
Установите соответствие между физическими величинами и их значениями. К каждой позиции первого столбца подберите соответствующую позицию второго столбца. 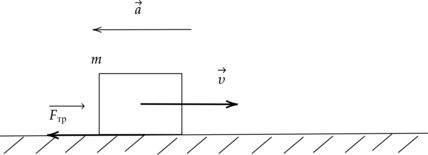 \[\begin{array}{cccccccc}
\text{ Физические величины}& & & & & & &\text{ Формулы}\\\\
\text{А) Коэффициент трения}& & & & & & & \text{ 1) } \displaystyle 0,1\\\\ & & & & & & &
\text{ 2) } \displaystyle 1\\\\
\text{Б) Время}& & & & & & & \text{ 3) } \displaystyle 0,4\\\\
& & & & & & &\text{ 4) } \displaystyle 4\\
\end{array}\] \[\begin{array}{|c|c|}
\hline
\text{А}&\text{Б}\\
\hline
&\\
\hline
\end{array}\]
\[\begin{array}{cccccccc}
\text{ Физические величины}& & & & & & &\text{ Формулы}\\\\
\text{А) Коэффициент трения}& & & & & & & \text{ 1) } \displaystyle 0,1\\\\ & & & & & & &
\text{ 2) } \displaystyle 1\\\\
\text{Б) Время}& & & & & & & \text{ 3) } \displaystyle 0,4\\\\
& & & & & & &\text{ 4) } \displaystyle 4\\
\end{array}\] \[\begin{array}{|c|c|}
\hline
\text{А}&\text{Б}\\
\hline
&\\
\hline
\end{array}\]
А) Воспользуемся вторым законом Нютона: \[\vec{F} = m\vec{a}\] \[-F_\text{тр}=m\cdot (-a)\] \[F_\text{тр}=ma\] Сила трения: \[F_\text{тр}=\mu N\] Так как на тело не действуют никакие силы, то \(N=mg\), тогда формула принимает вид: \[F_\text{тр}=\mu mg\] \[\mu =\dfrac{F_\text{тр}}{mg}=\dfrac{ma}{mg}=\dfrac{1\text{ м/с}^2}{10 \text{ м/с}^2}=0,1\] А — 1
Б) По второй формулировке закона Ньютона: \[F_{\text{тр}}=\dfrac{\Delta p}{\Delta t}\] \[t=\dfrac{\Delta p}{F_\text{тр}}=\dfrac{\Delta p}{ma}=\dfrac{(120-200)\text{ кг}\cdot \text{м/с}}{20 \text{ кг}\cdot (-1)\text{ м/с}^2}=4 \text{ c}\] Б — 4
Закрепленный пружинный пистолет стреляет вертикально вверх. Какую скорость приобрела пуля после выстрела, и какой была деформация пружины, если жесткость пружины \(k = 750\) H/м, а пуля массой \(m=0,25\) кг в результате выстрела поднялась на высоту \(h = 7\) м. Трением и сопротивлением воздуха пренебречь.
Установите соответствие между физическими величинами и формулами, по которымих можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго столбца. 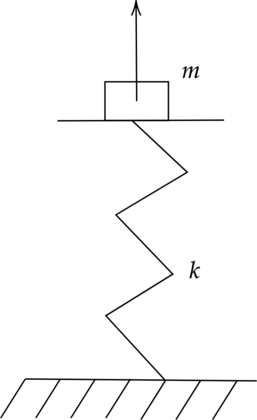 \[\begin{array}{cccccccc}
\text{ Физические величины}& & & & & & &\text{ Формулы}\\\\
\text{А) Деформация пружины, см}& & & & & & & \text{ 1) } \displaystyle 8\\\\ & & & & & & &
\text{ 2) } \displaystyle 26\\\\
\text{Б) Скорость бруска $V$ после выстрела}& & & & & & & \text{ 3) } \displaystyle 11,5\\\\
& & & & & & &\text{ 4) } \displaystyle 37\\
\end{array}\] \[\begin{array}{|c|c|}
\hline
\text{А}&\text{Б}\\
\hline
&\\
\hline
\end{array}\]
\[\begin{array}{cccccccc}
\text{ Физические величины}& & & & & & &\text{ Формулы}\\\\
\text{А) Деформация пружины, см}& & & & & & & \text{ 1) } \displaystyle 8\\\\ & & & & & & &
\text{ 2) } \displaystyle 26\\\\
\text{Б) Скорость бруска $V$ после выстрела}& & & & & & & \text{ 3) } \displaystyle 11,5\\\\
& & & & & & &\text{ 4) } \displaystyle 37\\
\end{array}\] \[\begin{array}{|c|c|}
\hline
\text{А}&\text{Б}\\
\hline
&\\
\hline
\end{array}\]
А) Закон сохранения энергии: \[\dfrac{k\Delta x^2}{2}=mgh\] \[\Delta x=\sqrt{\dfrac{2mgh}{k}}=\sqrt{\dfrac{2 \cdot 0,25 \text{ кг} \cdot 10 \text{ м/с}^2 \cdot 7 \text{ м}}{750 \,\text{ H/м}}}=0,37 \text{ м }\] А — 4
Б) Полная механическая энергия: \[E_\text{ пот}=E_\text{ кин}\] Пистолет сообщил пуле кинетическую энергию, благодаря которой она поднимается на расстояние \(L=h-\Delta x\). Тогда: \[\dfrac{mV^2}{2}=mgL\] \[V=\sqrt{\dfrac{2mgL}{m}}=\sqrt{2 \cdot 10 \text{ м/с}^2 \cdot (7-0,37) \text{ м}}=11,5 \text{ м/с}\] Б — 3
Башенный кран монотонно поднимает плиту массой \(m= 750\) кг за время \(t = 15\) c на высоту \(h=13\) м. Определите, какую работу совершил кран, и какую мощность он имеет.
Установите соответствие между физическими величинами и формулами, по которымих можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго столбца. \[\begin{array}{cccccccc} \text{ Физические величины}& & & & & & &\text{ Формулы}\\\\ \text{А) Работа, кДж}& & & & & & & \text{ 1) } \displaystyle 65\\\\ & & & & & & & \text{ 2) } \displaystyle 9,75\\\\ \text{Б) Мощность, }10^2\text{ Вт}& & & & & & & \text{ 3) } \displaystyle 97,5\\\\ & & & & & & &\text{ 4) } \displaystyle 50\\ \end{array}\] \[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline &\\ \hline \end{array}\]
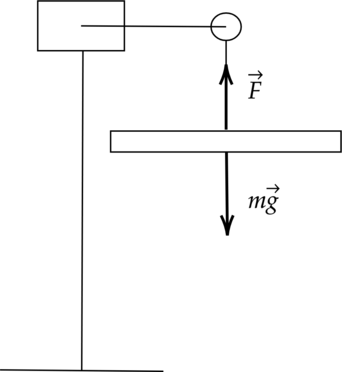
А) Автокран работает против силы тяжести. Тогда: \[A=E_\text{пот}=mgh=750\text{ кг}\cdot 10 \text{ м/с}^2 \cdot 13 \text{ м}=97500 \text{ Дж }\] А — 3
Б) Мощность: \[N = \dfrac{A}{t}= \frac{97500 \text{ Дж}}{15\text{ c}}=6500\text{ Вт }\] Б — 1
Бруску массой \(m\), лежащему у подножья горки, придают кинетическую энергию \(E_\text{кин}\). Он поднимается вдоль оси \(Ox\) на расстояние \(L\). Определите потенциальную энергию \(E_\text{пот}\) и ускорение \(a\), если \(\mu\) — коэффициент трения, \(\alpha\) — угол наклона горки. Сопротивлением воздуха пренебречь
Установите соответствие между физическими величинами и формулами, по которымих можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго столбца.
\[\begin{array}{cccccccc}
\text{ Физические величины}& & & & & & &\text{ Формулы}\\\\
\text{А) Потенциальная энергия}& & & & & & & \text{ 1) } \displaystyle g(\mu \cdot cos\alpha- sin\alpha)\\\\ & & & & & & &
\text{ 2) } \displaystyle g(\mu \cdot cos\alpha+ sin\alpha)\\\\
\text{Б) Ускорение}& & & & & & & \text{ 3) } \displaystyle E_\text{кин}- \mu mg \cdot L \cdot cos\alpha\\\\
& & & & & & &\text{ 4) } \displaystyle E_\text{кин}+ \mu mg\cdot L \cdot cos\alpha\\
\end{array}\] \[\begin{array}{|c|c|}
\hline
\text{А}&\text{Б}\\
\hline
&\\
\hline
\end{array}\]
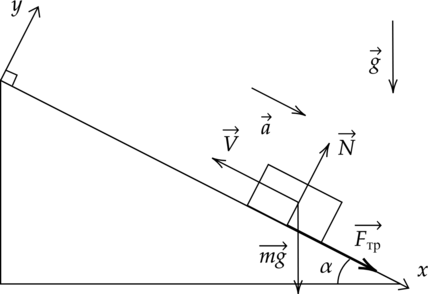
А) Так как на тело действует внешняя сила, то применим закон об изменении кинетической энергии: \[\Delta E_\text{кин}=A_{\text{тр}}+ A_{mg},\] где \(A_{\text{тр}}=F_\text{тр}\cdot L\cdot cos\beta=-F_\text{тр}\cdot L\), \(\beta=180^{\circ}\) — угол между вектором перемещения и силой трения. \[A_{mg}=0-E_\text{пот}\] \[\Delta E_\text{кин}=0-E_\text{кин}=-E_\text{кин}\] \[-E_\text{кин}=-E_\text{пот}-F_\text{тр}\cdot L\] \[E_\text{пот}=E_\text{кин}- F_\text{тр}\cdot L\] По второму закону Ньютона, спроецированному на ось \(Oy\) следует: \[N=mg \cdot cos\alpha,\] откуда \(F_\text{тр}=\mu mg \cdot cos\alpha\). Тогда: \[E_\text{пот}=E_\text{кин}- \mu mg \cdot cos\alpha \cdot L\] А — 3
Б) Воспользуемся вторым законом Ньютона: \[\vec{N}+m\vec{g}+\vec{F_\text{тр}}=m\vec{a}\] Спроецируем на ось \(Ox\): \[F_\text{тр}+mg\cdot sin\alpha=ma\] \[a=\dfrac{F_\text{тр}+mg\cdot sin\alpha}{m}=\dfrac{\mu mg \cdot cos\alpha+mg\cdot sin\alpha}{m}= g(\mu \cdot cos\alpha+ sin\alpha)\] Б — 2
Мяч массой \(M\) без трения катится со скоростью \(\upsilon\) по горизонтальной плоскости. После он абсолютно неупруго соударяется с бруском массой \(m\). Определите кинетическую энергию образовавшегося тела \(E_\text{кин}\) после столкновения и теплоту, которую выделили тела во время удара.
Установите соответствие между физическими величинами и формулами, по которымих можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго столбца. 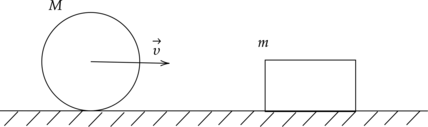 \[\begin{array}{cccccccc}
\text{ Физические величины}& & & & & & &\text{ Формулы}\\\\
\text{А) Кинетическая энергия}& & & & & & & \text{ 1) } \displaystyle \dfrac{(M\upsilon)^2}{2(M+m)}\\\\ & & & & & & &
\text{ 2) } \displaystyle \dfrac{mM\upsilon^2}{2(M+m)}\\\\
\text{Б) Выделившаяся теплота}& & & & & & & \text{ 3) } \displaystyle \dfrac{mM\upsilon^2}{2(M-m)}\\\\
& & & & & & &\text{ 4) } \displaystyle \dfrac{({M\upsilon}+m\upsilon)^2}{2M}\\
\end{array}\] \[\begin{array}{|c|c|}
\hline
\text{А}&\text{Б}\\
\hline
&\\
\hline
\end{array}\]
\[\begin{array}{cccccccc}
\text{ Физические величины}& & & & & & &\text{ Формулы}\\\\
\text{А) Кинетическая энергия}& & & & & & & \text{ 1) } \displaystyle \dfrac{(M\upsilon)^2}{2(M+m)}\\\\ & & & & & & &
\text{ 2) } \displaystyle \dfrac{mM\upsilon^2}{2(M+m)}\\\\
\text{Б) Выделившаяся теплота}& & & & & & & \text{ 3) } \displaystyle \dfrac{mM\upsilon^2}{2(M-m)}\\\\
& & & & & & &\text{ 4) } \displaystyle \dfrac{({M\upsilon}+m\upsilon)^2}{2M}\\
\end{array}\] \[\begin{array}{|c|c|}
\hline
\text{А}&\text{Б}\\
\hline
&\\
\hline
\end{array}\]
А) Если тела абсолютно неупруго соударяются, то они слипаются, двигаясь с общей скоростью \(V\). Закон сохранения импульса: \[M\upsilon=(M+m)V\] \[V=\dfrac{M\upsilon}{M+m}\] Кинетическая энергия: \[E_\text{кин}=\dfrac{(M+m)V^2}{2}=\dfrac{(M+m)\left( \dfrac{M\upsilon}{M+m}\right) ^2}{2}=\dfrac{\dfrac{(M\upsilon)^2}{M+m}}{2}=\dfrac{(M\upsilon)^2}{2(M+m)}\] А — 1
Б) Из-за абсолютно неупругого столкновения ЗСЭ не выполняется, так как выделяется тепло \(Q\), тогда: \[E_\text{кин1}=Q+E_\text{кин2}\] \[Q=E_\text{кин1}-E_\text{кин2}=\dfrac{M\upsilon^2}{2}-\dfrac{(M\upsilon)^2}{2(M+m)}=\dfrac{M(M+m)\upsilon^2}{2(M+m)}-\dfrac{(M\upsilon)^2}{2(M+m)}\] \[Q=\dfrac{M(M+m)\upsilon^2-(M\upsilon)^2}{2(M+m)}=\dfrac{mM\upsilon^2}{2(M+m)}\] Б — 2
Снайпер массой \(M=75\) кг, стоящий на скользкой горизонтальной поверхности, стреляет из винтовки в направлении оси \(Ox\). Масса снаряда \(m= 0,01\) кг. Снаряд пролетает расстояние \(L=3500 \) м с замедляющим ускорением \(a=70\) м/с\(^2\). Определите скорость снайпера и кинетическую энергию пули после выстрела.
Установите соответствие между физическими величинами и формулами, по которымих можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго столбца. \[\begin{array}{cccccccc} \text{ Физические величины}& & & & & & &\text{ Формулы}\\\\ \text{А) Скорость снайпера, мм/с}& & & & & & & \text{ 1) } \displaystyle 75\\\\ & & & & & & & \text{ 2) } \displaystyle 54\\\\ \text{Б) Кинетическая энергия, }10^2 \text{ Дж}& & & & & & & \text{ 3) } 24,5\\\\ & & & & & & &\text{ 4) } \displaystyle 90\\ \end{array}\] \[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline &\\ \hline \end{array}\]
А) ЗСИ: \[0=mU-MV\] \[MV=mU,\] где \(V\) — скорость снайпера, \(U\) — скорость пули. Воспользуемся кинематикой для рассчета скорости пули: \[S=\dfrac{0-U^2}{-2a}\] \[U=\sqrt{2Sa}\] Подставим неизвестные величины в ЗСИ: \[V=\dfrac{mU}{M}=\dfrac{m\sqrt{2Sa}}{M}=\dfrac{0,01\text{ кг}\sqrt{2\cdot 3500 \text{ м} \cdot 70\text{ м/с}^2}}{ 75 \text{ кг}}=0,09 \text{ м/с}\] А — 4
Б) Кинетическая энергия: \[E_\text{кин}=\dfrac{mU^2}{2}=\dfrac{m(\sqrt{2Sa})^2}{2}=\dfrac{0,01 \text{ кг}\cdot 2\cdot 3500 \text{ м} \cdot 70\text{ м/с}^2}{2}=2450 \text{ Дж }\] Б — 3



