12. МКТ и Термодинамика (изменение физических величин в процессах, установление соответствия) (страница 2)
Готовиться с нами - ЛЕГКО!

Идеальный одноатомный газ постоянной массы переходит из состояния 1 в состояние 2 (см. pT-диаграмму). Как в ходе этого процесса изменятся объём газа и его внутренняя энергия? 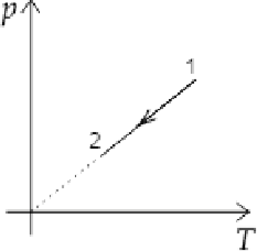
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|} \hline \text{Объем}&\text{Внутренняя энергия}\\ \text{газа}&\text{газа}\\ \hline & \\ \hline \end{array}\]
По диаграмме можно определить, что рассматриваемый процесс — изохорный. Значит, объём газа в ходе процесса не изменяется.
Внутреннюю энергию газа можно найти по формуле: \[U=\dfrac{3}{2}\nu RT,\] где \(\nu=const\), т.к. масса газа постоянна по условию.
Отсюда \(U \sim T\). По диаграмме находим, что \(T\) в данном процессе уменьшается, значит и внутренняя энергия газа также уменьшается.
На рисунке показан процесс изменения состояния 1 моля одноатомного идеального газа (\(U\) — внутренняя энергия газа; \(V\) — занимаемый им объем). Как изменятся в ходе этого процесса давление и абсолютная температура газа? 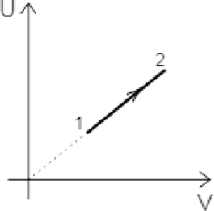
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|} \hline \text{Давление газа}&\text{Температура газа}\\ \hline & \\ \hline \end{array}\]
Внутреннюю энергию газа можно найти по формуле: \[U=\dfrac{3}{2}\nu RT,\] Отсюда \(U \sim T\). По диаграмме находим, что \(U\) в данном процессе увеличивается, значит и абсолютная температура газа также увеличивается.
Т.к. \(U\) связано с температурой линейно, то по диаграмме определяем: \[\dfrac{U}{V}=const~\Rightarrow~\dfrac{T}{V}=const\] Значит рассматриваемый процесс — изобарный. А в изобарном процессе \(p=const\). Давление в ходе процесса не изменяется.
Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не изменяется. Как изменяются при этом объём газа и его внутренняя энергия? 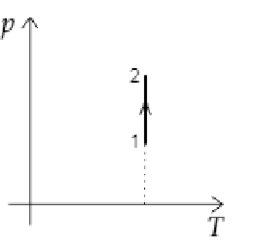
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|} \hline \text{Объем газа}&\text{Внутренняя энергия газа}\\ \hline & \\ \hline \end{array}\]
Изменение внутренней энергии газа можно найти по формуле: \[\Delta U=\dfrac{3}{2}\nu \Delta T,\] где \(\nu=const\), т.к. масса газа постоянна по условию.
По диаграмме видно, что температура газа постоянна, т.е. \(\Delta T=0\). Значит внутренняя энергия газа не изменяется.
Т.к. по условию температура и масса газа не изменяются, рассматриваемый процесс является изотермическим.
По закону Бойля-Мариотта: \[pV=const~\Rightarrow~p\sim\dfrac{1}{V}\] По диаграмме определяем, что давление газа увеличивается. Значит, объем газа уменьшается.
Идеальный газ совершает два процесса. В процессе 1 газ сначала нагревался при постоянном давлении, потом его давление увеличивалось при постоянном объеме, затем при постоянной температуре давление газа уменьшилось до первоначального значения. В процессе 2 объем газа с давлением сначала увеличивались, затем его объем уменьшался при постоянном давлении, потом давление газа уменьшалось при постоянном объеме и газ вернулся в первоначальное состояние. Какие из графиков в координатных осях \(p - V\) соответствует этим изменениям состояния газа? 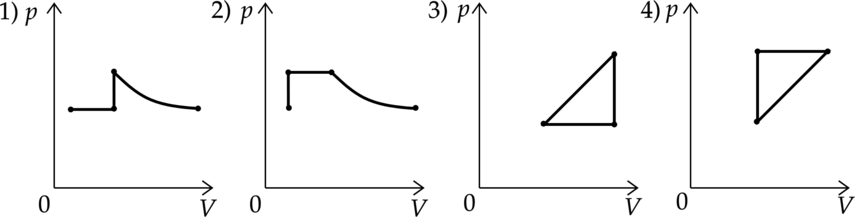
Запишите в таблицу выбранные цифры для каждого процесса в указанном порядке. \[\begin{array}{|c|c|c|}
\hline
\text{ Процесс } 1&\text{ Процесс }2\\
\hline
&\\
\hline
\end{array}\]
Распишем, как должны выглядеть процессы в координатах \(p-V\).
Процесс 1:
Газ сначала нагревался при постоянном давлении, значит на графике это будет горизонтальная прямая. Потом его давление увеличивалось при постоянном объеме — это будет вертикальная прямая. Затем при постоянной температуре давление газа уменьшилось до первоначального значения — на графике это будет гипербола.
Нам подходит первый вариант.
Процесс 2:
Объем газа с давлением сначала увеличивались, значит на графике это прямая, направленная под углом к осям. Затем его объем уменьшался при постоянном давлении — на графике это будет горизонтальная прямая. Потом давление газа уменьшалось при постоянном объеме – это будет вертикальная прямая.
Нам подходит график 4.
Идеальный газ совершал два процесса. В процессе 1 газ сначала охлаждался при постоянном давлении, потом его давление уменьшалось при постоянном объеме, затем при увеличении температуры давление газа увеличилось до первоначального значения. В процесс 2 газ сначала давление газа уменьшалось при постоянной температуре, потом газ расширялся при постоянном давлении, затем увеличивал давление до первоначального, при постоянном объеме. Какие из графиков в координатных осях \(p-V\) соответствует этим изменениям состояния газа? 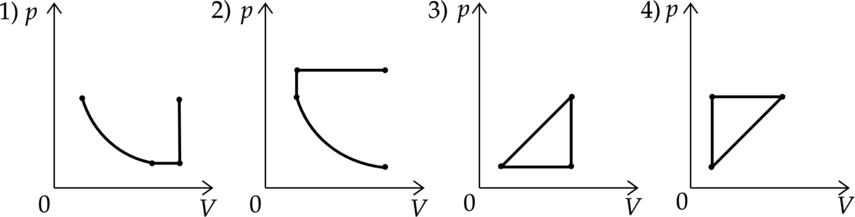
Запишите в таблицу выбранные цифры для каждого процесса в указанном порядке. \[\begin{array}{|c|c|c|}
\hline
\text{ Процесс } 1&\text{ Процесс }2\\
\hline
&\\
\hline
\end{array}\]
Распишем, как должны выглядеть процессы в координатах \(p-V\).
Процесс 1:
Газ сначала охлаждался при постоянном давлении — горизонтальная прямая. Потом его давление уменьшалось при постоянном объеме — вертикальня прямая. Затем при увеличении температуры давление газа увеличилось до первоначального значения — прямая, направленная под углом к осям.
Это график 4.
Процесс 2:
Сначала давление газа уменьшалось при постоянной температуре — гипербола. Потом газ расширялся при постоянном давлении — горизонтальная прямая. Затем увеличивал давление, до первоначального, при постоянном объеме — вертикальная прямая.
Таким образом, нам подходит вариант 1.
В сосуде неизменного объема находится идеальный газ. Часть газа выпускали из сосуда так, что давление оставалось неизменным. Как изменились при этом температура газа, оставшегося в сосуде, и количество вещества?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
\[\begin{array}{|c|c|c|} \hline \text{ Температура газа}& \text{ Количество вещества}\\ \hline & \\ \hline \end{array}\]
Температура — 1
1)Уравнение состояния газа: \[pV=\nu RT,\] где \(p\) — давление газа, \(V\) — объем, занимаемый газом, \(\nu\) — количество вещества газа, \(R\) — универасальная газовая постоянная, \(T\) — абсолютная температура.
Выразим температуру газа: \[T=\dfrac{pV}{\nu R}\] При уменьшении количества газа (\(V=const\), \(p=const\)) температура увеличится.
Количество вещества — 2
2) Так как из сосуда выпустили часть газа, то количество вещества уменьшилось.
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик. Из сосуда выпускается половина газа при неизменной температуре. Как изменится в результате этого объём газа и его давление?

Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться. \[\begin{array}{|c|c|c|}
\hline
\text{ Объем газа}&\text{ Давление}\\
\hline
&\\
\hline
\end{array}\]
Объем газа — 2
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлении. Уравнение состояния газа: \[pV=\nu RT,\] где \(p\) — давление газа, \(V\) — объем, занимаемый газом, \(\nu\) — количество вещества газа, \(R\) — универасальная газовая постоянная, \(T\) — абсолютная температура.
Выразим отсюда объем газа: \[V=\dfrac{\nu RT}{p}\] При уменьшении количества вещества газа (\(T=const\), \(p=const\)) его объем уменьшится.
2) Давление — 3



