Газовые законы
Готовиться с нами - ЛЕГКО!

1 моль гелия изохорно нагревают на 154 К, при этом давление газа увеличивается в 2,1 раза. До какой температуры нагрели газ? Ответ дайте в кельвинах.
Процесс изохорный, т.е. объём не меняется. Запишем закон Шарля: \[\hspace{ 5 mm} \dfrac{p_1}{T_1}=\dfrac{p_2}{T_2} \hspace{ 5 mm} (1)\] Изменение температуры есть разница конечной и начальной температуры газа: \[\hspace{ 5 mm} \Delta T = T_2 - T_1 \hspace{3 mm} \Rightarrow \hspace{3 mm} T_1 = T_2 - \Delta T \hspace{ 5 mm} (2)\] По условию давление газа увеличивается в 2,1 раза: \[\hspace{ 5 mm}p_2 = 2,1 p_1\hspace{ 5 mm} (3)\] Подставим (2), (3) в (1) и выразим температуру, до которой нагрели газ: \[\dfrac{p_1}{T_2 - \Delta T}=\dfrac{2,1 p_1}{T_2}\] \[T_2 = \dfrac{2,1 p_1 \Delta T}{2,1p_1 - p_1} = \dfrac{2,1 \Delta T}{1,1} = \dfrac{2,1 \cdot 154\text{ K}}{1,1} = 294 \text{ K}\]
Воздух при температуре 27\(^{\circ}\)C и давлении 202,65 кПа занимает объём 0,3 м\(^3\). Газ изобарно нагрели, причём объём газа увеличился до 0,5 м\(^3\). Найдите конечную температуру воздуха. Ответ дайте в кельвинах.
Т.к. процесс изобарный (\(p=const\)), используем закон Гей – Люссака: \[\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\hspace{3 mm}\Rightarrow \hspace{3 mm} T_2=\dfrac{T_1 \cdot V_2}{V_1}\] Переведём \(T_1\) в кельвины: 27\(^{\circ}\)С + 273 = 300 К. \[T_2=\dfrac{300 \text{ К} \cdot 0,5 \text{ м$^3$}}{0,3\text{ м$^3$}}=500 \text{ К}\]
На графике изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 1 равна 56\(^{\circ}\)C. Какова температура аргона в состоянии 2? Ответ дайте в кельвинах.

Из графика видно, что процесс 1–2 — изобарный (\(p=const\)). Воспользуемся законом Гей – Люссака: \[\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\hspace{3 mm}\Rightarrow \hspace{3 mm} T_2=\dfrac{T_1 \cdot V_2}{V_1}\] Переведём \(T_1\) в кельвины: 56\(^{\circ}\)С + 273 = 329 К. \[T_2=\dfrac{329\text{ К} \cdot 14\text{ м$^3$}}{7\text{ м$^3$}} = 658 \text{ К}\]
На графике изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 2 равна 212\(^{\circ}\)C. Какова температура аргона в состоянии 1? Ответ дайте в кельвинах.
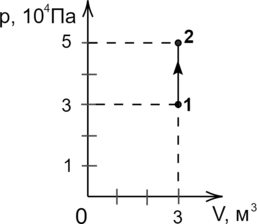
Из графика видно, что процесс 1–2 — изохорный (\(V=const\)). Воспользуемся законом Шарля: \[\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\hspace{3 mm}\Rightarrow \hspace{3 mm} T_1=\dfrac{p_1 \cdot T_2}{p_2}\] Переведём \(T_2\) в кельвины: 212\(^{\circ}\)С + 273 = 485 К. \[T_1=\dfrac{3\cdot 10^4 \text{ Па} \cdot 485\text{ К}}{5 \cdot 10^4\text{ Па}} = 291 \text{ К}\]
Давление газа при температуре 306 К равно 159 кПа. Газ нагрели до температуры \(T_2\), при этом объём газа не изменился. После нагревания давление газа стало равно 212 кПа. Найдите, до какой температуры \(T_2\) нагрели газ. Ответ дайте в кельвинах.
По условию процесс изохорный (\(V=const\)).
Согласно закону Шарля: \[\dfrac{p_1}{T_1} = \dfrac{p_2}{T_2}\hspace{3 mm}\Rightarrow\hspace{3 mm} T_2 = \dfrac{T_1 p_2}{p_1}\] \[T_2 = \dfrac{306 \text{ K} \cdot 212 \cdot 10^3 \text{ Па}}{159 \cdot 10^3 \text{ Па}} = 408 \text{ K}\]
Газ занимает объём 0,03 м\(^3\) при температуре 418 К. Какой объём займёт этот же газ, если его температура понизится до 209 К? Давление и масса газа не меняются. Ответ дайте в м\(^3\).
По условию процесс изобарный (\(p=const\)). По закону Гей – Люссака: \[\dfrac{V_1}{T_1} = \dfrac{V_2}{T_2}\hspace{3 mm}\Rightarrow\hspace{3 mm} V_2 = \dfrac{V_1T_2}{T_1}\] \[V_2 = \dfrac{0,03 \text{ м$^3$} \cdot 209 \text{ К}}{418 \text{ К}} = 0,015 \text{ м$^3$}\]
На рисунке представлен график зависимости давления от температуры газа. Объём газа в состоянии 2 равен 6 л. Какой объём занимает газ в состоянии 1? Масса газа не меняется. Ответ дайте в м\(^3\).
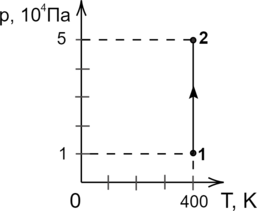
По графику видно, что процесс 1–2 — изотермический (\(T=const\)). По закону Бойля – Мариотта: \[p_1V_1 = p_2V_2\hspace{3 mm}\Rightarrow\hspace{3 mm} V_1 = \dfrac{p_2V_2}{p_1}\] Переведём объём газа в м\(^3\): \(\; \;\) 6 л = 6 \(\cdot\) 10\(^{-3}\) м\(^3\). \[V_1 = \dfrac{5 \cdot 10^{4} \text{ Па} \cdot 6 \cdot 10^{-3} \text{ м$^3$}}{1 \cdot 10^{4} \text{ Па}} = 0,03 \text{ м$^3$}\]



