10. Реальные газы. Тепловые явления (страница 3)
Готовиться с нами - ЛЕГКО!

На рисунке показана зависимость температуры \(T\) от выделенной теплоты \(Q\) для 0,8 кг первоначально газообразного вещества. Найдите удельную теплоту парообразования вещества. Ответ дайте в кДж/кг. 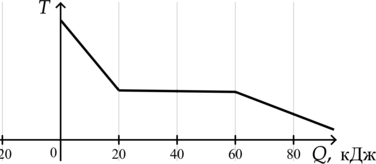
В процессе конденсации температура вещества не меняется. На графике есть лишь один такой кусок в промежутке от 20 кДж до 60 кДж. Следовательно, за весь процесс конденсации выделяется количество теплоты: \[Q = Q_{2} - Q_{1} = 60 \text{ кДж} - 20 \text{ кДж} = 40 \text{ кДж}\] По формуле количества теплоты: \[Q = rm\] \[r = \dfrac{Q}{m} = \dfrac{40 \text{ кДж}}{0,8 \text{ кг}} = 50 \text{ кДж/кг}\]
Найдите удельную теплоемкость вещества массой 2,5 кг по графику зависимости температуры от количества теплоты. Ответ дайте в \(\dfrac{\text{Дж}}{\text{кг$\cdot$К }}\).
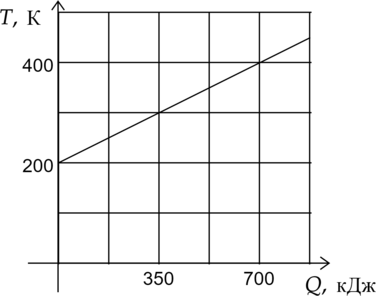
Проанализируем график. Каждый раз, как температура увеличивается на 100 К, количество теплоты возрастает на 350 кДж. Тогда по формуле количества теплоты: \[Q = cm\Delta t\] \[c = \dfrac{Q}{m\Delta t} = \dfrac{350 \cdot 10^{3} \text{ Дж}}{2,5 \text{ кг} \cdot 100 \text{ К}} = 1,4 \cdot 10^{3} \dfrac{\text{Дж}}{\text{кг$\cdot$К }} = 1400 \dfrac{\text{Дж}}{\text{кг$\cdot$К }}\]
Андрей решил провести опыт. Он сообщил чугунной сковородке массой 3 кг определенное количество теплоты, в результате чего сковородка нагрелась от 290 К до 333 К. Какое количество теплоты сообщил сковородке Андрей? Ответ дайте в кДж
По формуле количества теплоты для нагрева вещества: \[Q = cm\Delta t = cm(t_{2} - t_{1}) = 500 \dfrac{\text{Дж}}{\text{кг$\cdot$К }} \cdot 3 \text{ кг} \cdot (333 \text{ К} - 290 \text{ К}) = 64500 \text{ Дж} = 64,5 \text{ кДж}\]
Помощнику кузнеца дали задание переплавить кусок свинца массой 3,7 т. Какое количество теплоты для этого потребуется? Свинец находится при температуре плавления. Ответ дайте в МДж.
По формуле количества теплоты плавления: \[Q = \lambda m = 2,5 \cdot 10^{4} \text{ Дж/кг} \cdot 3,7 \cdot 10^{3} \text{ кг} = 9,25 \cdot 10^{7} \text{ Дж} = 92,5 \text{ МДж}\]
Определите удельную теплоту плавления изначально твердого вещества массой 4 кг по графику зависимости количества теплоту \(Q\) от температуры \(t\). Ответ укажите в кДж/кг. 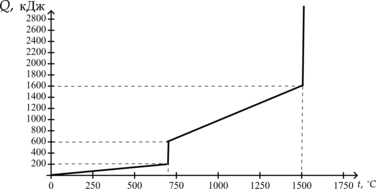
Проанализируем график. В промежутке от \(0^\circ\)С до \(700^\circ\)С твердое тело нагревают. Как только график достигает отметки в \(700^\circ\)С, тело начинает плавиться до тех пор, пока количество теплоты не достигнет отметки в 600 кДж/кг. После этого начинается нагрев жидкости вплоть до \(1500^\circ\)С. Как только график достигает значения в \(1500^\circ\)С, начинается процесс парообразования, который продолжается вплоть до конца графика. Таким образом, необходимый нам промежуток находятся от 200 кДж до 600 кДж. То есть, на плавление было затрачено: \[Q = 600 \text{ кДж} - 200 \text{ кДж} = 400 \text{ кДж} = 400 \cdot 10^{3} \text{ Дж}\] По формуле количества теплоты плавления: \[Q = \lambda m\] \[\lambda = \dfrac{Q}{m} = \dfrac{400 \cdot 10^{3} \text{ Дж/кг}}{4} = 100 \cdot 10^{3} \text{ Дж/кг} = 100 \text{ кДж/кг}\]
Учитель бросает в калориметр с водой массой 4 кг и температурой \(t_{1} = 0^\circ\)C кусок льда массой 0,5 кг при температуре \(t_{2} = -99^\circ\)C. Дождавшись, пока в калориметре установится тепловое равновесие, учитель измерил массу льда в калориметре. Какое значение получил учитель? Ответ дайте в граммах.
Обозначим температуру теплового равновесия за \(t_{3}\). По уравнению теплового баланса: : \[Q_\text{в} = Q_\text{л}\] Проверим, какое количество теплоты выделяется при кристализации воды и при нагревании льда до \(0^\circ\)C: \[Q_\text{в} = \lambda m_\text{в} = 330 \cdot 10^{3} \text{ Дж/кг} \cdot 4 \text{ кг} = 1320 \cdot 10^{3} \text{ Дж} = 1320 \text{ кДж}\] \[Q_\text{л} = cm_\text{л}(t_{1} - t_{2}) = 2100 \dfrac{\text{Дж}}{\text{кг$\cdot$К }}\cdot 0,5 \text{ кг} \cdot (0^\circ \text{С} - (-99^\circ \text{С})) = 103950 \text{ Дж} = 103, 95 \text{ кДж}\] Количество теплоты, выделившиеся при кристализации воды намного больше, чем количество теплоты для нагрева льда, следовательно, тепловое равновесие наступит при \(0^\circ\)C, а вода выделит на нагрев льда количество теплоты численно равное значению \(Q_{л}\). В процессе этого часть воды превратится в лёд, то есть: \[Q_\text{л} = \lambda m_\text{пр.в.}\] \[m_\text{пр.в.} = \dfrac{Q_\text{л}}{\lambda} = \dfrac{103950 \text{ Дж}}{330 \cdot 10^{3} \text{ Дж/кг}} = 0,315 \text{ кг} = 315 \text{ г}\] Общая масса льда в калориметре: \[m = m_\text{пр.в.} + m_\text{л} = 315 \text{ г} + 500 \text{ г} = 815 \text{ г}\]
Кузнец дал своему помощнику задание расплавить кусок алюминия, изначально находящийся при температуре \(t_{1} = 60,3^\circ\)C. Через 18 с алюминий достиг температуры плавления \(t_{2} = 660,3^\circ\)C. Сколько секунд понадобится помощнику, чтобы расплавить этот кусок, находящийся при температуре плавления? Удельная теплота плавления алюминия 390 кДж/кг.
По формуле мощности нагревателя: \[P = \dfrac{A}{\tau}\] Мощность нагревателя остается неизменной, т.е. меняется только работа \(A\) и время, на неё затраченное. То есть: \[P = \dfrac{Q_\text{нагр}}{\tau_\text{нагр}} = \dfrac{Q_\text{пл}}{\tau_\text{пл}}\] По формуле количества теплоты нагрева: \[Q_\text{нагр} = cm\Delta t = cm(t_{2} - t_{1})\] По формуле количества теплоты плавления: \[Q_\text{пл} = \lambda m\] Из имеющихся данных найдем время плавления \(\tau_\text{пл}\): \[\tau_\text{пл} = \dfrac{Q_\text{пл}\tau_\text{нагр}}{Q_\text{нагр}} = \dfrac{\lambda m\tau_\text{нагр}}{cm(t_{2} - t_{1})} =\dfrac{\lambda \tau_\text{нагр}}{c(t_{2} - t_{1})} = \dfrac{390 \cdot 10^{3} \text{ Дж/кг} \cdot 18 \text{ с}}{900 \dfrac{\text{Дж}}{\text{кг$\cdot$К }} \cdot (660,3^\circ C - 60,3^\circ C)} = 13 \text{ с}\]



