Момент силы, механическое равновесие тела (страница 2)
Готовиться с нами - ЛЕГКО!

К рычагу подвешены два груза массами \(m_1 = 2\) кг и \(m_2 = 0,5\) кг так, что он находится в равновесии. Длину плеча \(d_1\) увеличили в 3 раза. На сколько должна измениться масса второго груза, чтобы равновесие рычага не нарушилось? (Ответ дайте в килограммах.)
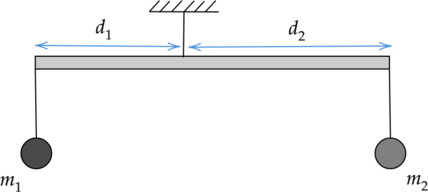
Так как рычаг после увеличения длины плеча \(d_1\) в 3 раза остается в равновесии, то моменты сил, действующих на него справа и слева во втором случае, должны быть равны: \(M_1 = M_2\).
В то же время моменты сил \(M_1\) и \(M_2\) по определению равны произведению силы на ее плечо: \[M_1 = F_1\cdot{3d_1}\] \[M_2 = F_2\cdot{d_2}\]
Отсюда получаем: \(F_1\cdot{d_1} = F_2\cdot{d_2}\)
На оба груза действует единственная сила – сила тяжести, поэтому: \[F_1 = m_1g\] \[F_2 = m_2^{'}g,\] где \(m_2^{'}\) – масса груза, подвешенного справа, во втором случае.
С учетом этого: \(M_1 = m_1g\cdot{3d_1}\) и \(M_2 = m_2^{'}g\cdot{d_2}\).
Приравняв \(M_1\) и \(M_2\), получаем, что: \[m_1g\cdot{3d_1} = m_2^{'}g\cdot{d_2}\] \[3m_1d_1 = m_2^{'}d_2\] Выразим массу второго груза \(m_2^{'}\): \[\displaystyle{m_2^{'} = \frac{3m_1d_1}{d_2}}\] Заметим, что \(\displaystyle{\frac{m_1d_1}{d_2} = m_1}\) (это следует из условия равновесия рычага для первого случая). \[m_2^{'} = 3m_1\] То есть, чтобы рычаг после увеличения длины плеча \(d_1\) в 3 раза сохранил равновесие, масса второго груза должна так же увеличиться в 3 раза.
Тогда его масса должна измениться на: \[\Delta m = m_2^{'} - m_2 = 3m_2 - m_2 = 2m_2\] \[\Delta m = 2\cdot{0,5\text{ кг}} = 1\text{ кг }\]
Какую силу \(F\) необходимо приложить, чтобы груз массой \(m = 6\) кг двигался вверх без ускорения, если радиус вала ворота \(R = 24\) см, а длина рукоятки \(l = 0,36\) м. Трением пренебречь. (Ответ дайте в Ньютонах.)
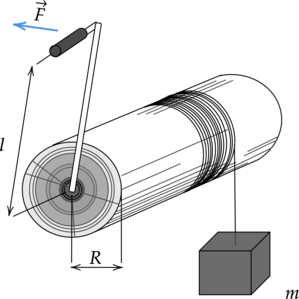
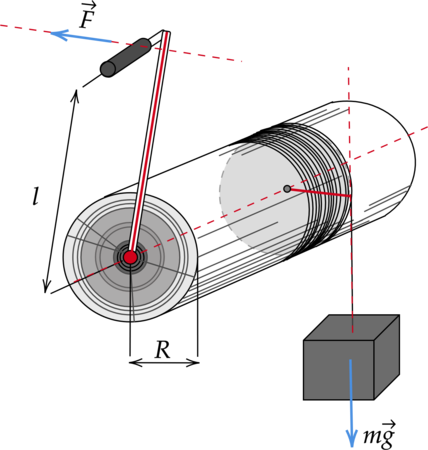
Т.к. груз движется без ускорения, то равнодействующая всех сил, действующих на груз, равна нулю. Поворот ворота обеспечивает подъем груза. В результате этого создается момент силы \(F\), длина плеча которой совпадает с длиной рукоятки \(l\), и он равен: \[M_1 = Fl\] Момент \(M_1\) уравновешивается моментом действующей на груз силы тяжести, длина плеча которой совпадает с радиусом вала ворота \(R\): \[M_2 = mg\cdot{R}\] \[Fl = mg\cdot{R}\] Отсюда выразим силу \(F\): \[\displaystyle{F = \frac{mg\cdot{R}}{l}}\] \[\displaystyle{F = \frac{6\text{ кг}\cdot{10\text{ м/c}^2}\cdot{0,24\text{ м}}}{0,36\text{ м}} = 40\text{ Н }}\]
На однородный прут со стороны горизонтальной поверхности действует сила трения, равная 20 Н. Найдите момент силы реакции опоры, действующей на него со стороны вертикальной поверности, относительно оси, проходящей через точку \(B\) перпендикулярно плоскости рисунка, если \(BC = 16\) см, а \(AC = 65\) см. (Ответ дайте в Н\(\cdot\)м и округлите до целого числа.) 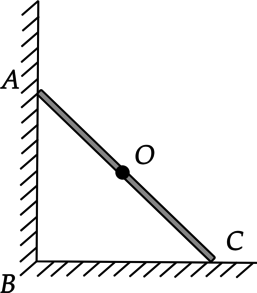
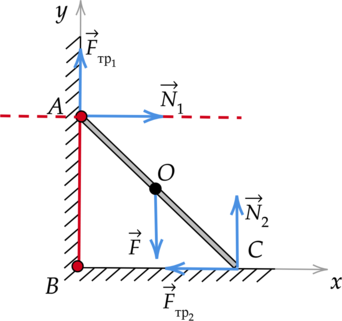
Момент действующей на вертикальную стенку силы реакции опоры относительно оси, перпендикулярной плоскости рисунка и проходящей через точку \(B\), равен: \[M = N_1l,\] где \(l\) - плечо силы. Мысленно продолжим линию действия силы реакции опоры \(N_1\) и перпендикуляром соединим ее с прямой, проходящей через точку \(B\). Получаем, что плечом силы \(N_2\) является отрезок \(AB\), равный: \[\displaystyle{AB = \sqrt{AC^2 - BC^2}}\] \[AB = \sqrt{0,65\text{ м}^2 - 0,16\text{ м}^2} = 0,63\text{ м }\] Чтобы найти неизвестную величину \(N_1\), укажем все силы, действующие на прут, и запишем второй закон Ньютона с учетом того, что тело находится в равновесии: \[\vec{F}_{\text{тр}1} + \vec{N}_1 + \vec{F} + \vec{N}_2 + \vec{F}_{\text{тр}2} = 0\] Введем оси \(OX\) и \(OY\), спроецируем на них все силы. \[OX: N_1 - F_{\text{тр}2} = 0\] \[OY: F_{\text{тр}1} + N_2 - F = 0\] Выразим силу реакции опоры \(N_1\), действующую на горизонтальную стенку: \[N_1 = F_{\text{тр}2}\] \[N_1 = 20\text{ H}\] Подставим найденные значения в начальную формулу: \[M = 20{\text{ Н}\cdot{0,63}\text{ м}} = 12,6\text{ Н}\cdot{\text{м}}\approx{13}\text{ Н}\cdot{\text{м }}\]
На однородный прут со стороны вертикальной поверхности действует сила реакции опоры, равная 125 Н. Найдите момент силы трения, действующей на него со стороны горизонтальной поверности, относительно оси, проходящей через точку \(A\) перпендикулярно плоскости рисунка, если \(BC = 39\) см, а \(AC = 89\) см. (Ответ дайте в кН\(\cdot\)м.) 
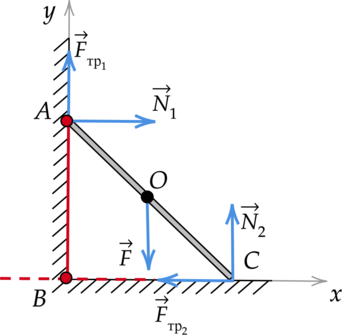
Момент действующей на прут со стороны горизонтальной стенки силы трения относительно оси, перпендикулярной плоскости рисунка и проходящей через точку \(A\), равен: \[M = F_{\text{тр}2}l,\] где \(l\) - плечо силы. Мысленно продолжим линию действия силы реакции опоры \(F_{\text{тр}2}\) и перпендикуляром соединим ее с прямой, проходящей через точку \(A\). Получаем, что плечом силы \(F_{\text{тр}2}\) является отрезок \(AB\), равный: \[\displaystyle{AB = \sqrt{AC^2 - BC^2}}\] \[AB = \sqrt{0,89\text{ м}^2 - 0,39\text{ м}^2} = 0,8\text{ м}\] Чтобы найти неизвестную величину \(F_{\text{тр}2}\), укажем все силы, действующие на прут, и запишем второй закон Ньютона с учетом того, что тело находится в равновесии: \[\vec{F}_{\text{тр}1} + \vec{N}_1 + \vec{F} + \vec{N}_2 + \vec{F}_{\text{тр}2} = 0\] Введем оси \(OX\) и \(OY\), спроецируем на них все силы. \[OX: N_1 - F_{\text{тр}2} = 0\] \[OY: F_{\text{тр}1} + N_2 - F = 0\] Выразим силу трения \(F_{\text{тр}2}\), действующую на горизонтальную стенку: \[F_{\text{тр}2} = N\] \[F_{\text{тр}2} = 125\text{ H }\] Подставим найденные значения в начальную формулу: \[M = 125{\text{ Н}\cdot{0,8}\text{ м}} = 100\text{ Н}\cdot{\text{м}} = 0,1\text{ кН}\cdot{\text{м }}\]
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

“Демоверсия 2018”
Из правила моментов: \[m1gl_1=m_2gl_2 \Rightarrow l_2=m_1\dfrac{l_1}{l_2}=0,2\text{ кг}\cdot 1,5=0,3\text{ кг}\] где \(m_1\) и \(m_2\) – массы грузов, \(l_1\) и \(l_2\) – расстояния от точки крепления грузов до точки подвеса.
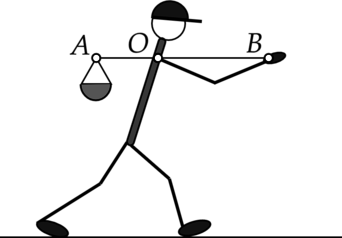
Человек несёт груз на лёгкой палке (см. рисунок). Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA. Ответ дайте в см.
“Демоверсия 2020”
Из правила моментов: \[F_1 \cdot OA=F_2 \cdot OB \Rightarrow OA= \dfrac{F_2\cdot OB}{F_1}=\dfrac{30\text{ Н}\cdot 80\text{ см}}{80\text{ Н}}=30\text{ см}\] Где \(F_1\) и \(F_2\) – силы, приложенные к концам ОА и ОВ соответственно.


