Волны
Готовиться с нами - ЛЕГКО!

Волновой процесс — любое изменение состояния сплошной среды, распространяющееся со скоростью и несущее энергию.
Поперечные волны — волны, при распространении которых смещение частиц среды происходит в направлении, перпендикулярном распространению волны.
— волна, при распространении которой смещение частиц среды происходит в направлении распространения волны.
Длина волны \(\lambda\) — расстояние между двумя ближайшими друг другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Единицы измерения: \(\displaystyle [\text{м}]\)
Скорость распространения волны
\[\displaystyle v=\dfrac{\lambda}{T}=h\nu\]
где \(T\) — период колебаний, \(\nu\) — частота колебаний.
Поскольку для всех электромагнитных волн скорость в вакууме (\(c\)) одинакова, по частоте легко определить длину волны \(\lambda\):
\[\lambda=\dfrac{c}{\nu}\]
Канатоходец заметил, что, когда он наступает на канат, то он выглядит так, как показано на рисунке, а скорость распространения волны 3 м/с. Найдите частоту колебаний.
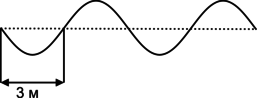
По рисунку видно, что половина длины волны равна 3 метра, значит длина волны равна 6 м.
По формуле найдем частоту: \[\displaystyle \nu=\frac{\upsilon}{\lambda}=\frac {3\text{ м/с}}{6\text{ м}}=0,5\text{ Гц}\]
Струна гитары издает звуковые волны с максимальной частотой \(\nu_1=40\) Гц, а струна балалайки \(\nu_2=120\) Гц. Найдите отношение длин волн \(\dfrac{\lambda_1}{\lambda_2}\).
Частота находится по формуле: \[\nu=\dfrac{\upsilon}{\lambda}\]
Выразим \(\lambda\): \[\lambda=\frac{\upsilon}{\nu}\]
Значит, \[\dfrac{\lambda_1}{\lambda_2}=\dfrac{\dfrac{\upsilon_1}{\nu_1}}{\dfrac{\upsilon_2}{\nu_2}}\]
Так как звук в одной среде распространяется с одинаковой скоростью, то \(\upsilon_1=\upsilon_2\), следовательно \[\frac{\lambda_1}{\lambda_2}=\frac{\nu_2}{\nu_1}=\frac{120\text{ Гц}}{40\text{ Гц}}=3\]
Пчела совершает 600 взмахов крыльев в минуту. Найдите период колебания крыльев. (Ответ дайте в секундах)
Период найдем по формуле: \[T=\dfrac{1}{\nu}\]
Где \(\nu\) — частота колебаний.
Частоту колебаний найдем по формуле: \[\displaystyle \nu=\dfrac{n}{t}\]
где \(n\) – количество взмахов, \(t\) – время, за которое совершается данное количество взмахов.
Переведем взмахи/минуту в взмахи/секунду \[600\text{ взмах/минут}=10\text{ взмах/секунд}\Rightarrow\]
Частота колебаний равна 10 Гц. Найдем период: \[T=\dfrac{1}{\nu}=\frac{1}{ 10 \text{ Гц}}=0,1\text{ с}\]
Отношение длин волн в средах 1 и 2 \(\dfrac{\lambda_1}{\lambda_2}=2\), а отношение частот \(\dfrac{\nu_1}{\nu_2}=1\). Найдите отношение времен \(\dfrac{t_1}{t_2}\), за которые звуковые волны проходят расстояние \(S\)?
Время рассчитыватся по формуле \(\displaystyle t=\frac{S}{\upsilon}\), где \(\upsilon\) – скорость. Значит: \[\frac{t_1}{t_2}=\dfrac{\dfrac{S}{\upsilon_1}}{\dfrac{S}{\upsilon_2}}=\frac{\upsilon_2}{\upsilon_1} \quad (1)\]
Формула для нахождение скорости: \[\displaystyle \upsilon=\lambda \cdot \nu\]
Значит, \[\displaystyle \upsilon_1=\lambda_1 \cdot \nu_1 \quad(2)\] \[\displaystyle \upsilon_2=\lambda_2 \cdot \nu_2 \quad(3)\]
Подставим (2) и (3) в (1) \[\frac{t_1}{t_2}=\frac{\lambda_2 \cdot \nu_2}{\lambda_1 \cdot \nu_1}=0,5\]
Муха крыльями совершает 300 колебаний за 2 минуты. Найдите частоту колебания крыльев. (Ответ дайте в Гц)
Формула для расчета частоты: \[\nu=\frac{n}{t}\]
Где \(n\) – количество колебаний, а \(t\) – время за которое совершили данное количество колебаний.
Переведем время в СИ: 2 минуты=120 секунд.
Посчитаем частоту: \[\nu=\frac{n}{t}=\frac{300}{120\text{ с}}=2,5\text{ Гц }\]
Колеблющаяся струна издает звук с длиной волны \(\lambda=2,72\) м. Найдите частоту колебаний, если скорость звука \(\upsilon=340\) м/с. (Ответ дайте в Гц)
Формула для расчета частоты \[\nu=\frac{\upsilon}{\lambda}=\frac{340\text{ м/c}}{2,72\text{ м}}=125\text{ Гц }\]
Петя стоит на расстоянии \(S=165\) м от горы и говорит в громкоговоритель. Найдите время, через которое Петя вновь услышит себя. Скорость звука принять 330 м/c. (Ответ дайте в секундах.)
Звук сначала дойдет до горы, потом отразится от горы и вновь дойдет до Пети. Значит он пройдет \(2S\), обозначим это расстояние \(S_\text{полн}\), а двигаться будет равномерно. Чтобы посчитать время будем использовать формулу \[t=\frac{S_\text{полн}}{\upsilon}\]
Где \(\upsilon\) – скорость звука
\[t=\frac{S_\text{полн}}{\upsilon}=\frac{2S}{\upsilon}=\frac{2\cdot 165 \text{ м}}{330\text{ м/с}}=1 \text{ с}\]



