физика (страница 4)

При прямолинейном движении зависимость координаты тела \(x(t)\) имеет вид: \(x(t)=5+2t+4t^2\). Найдите координату, скорость и ускорение в момент времени \(t=2\) c при таком движении?
1 способ:
Проекция скорости — это производная соответствующей координаты по времени, проекция ускорения — это производная скорости по времени: \[\upsilon_x=x'(t)=(5+2t+4t^2)'=2+8t\] \[a_x=\upsilon_x'(t)=(2+8t)'=8\] Зная зависимость скорости и ускорения от времени, найдем координату, скорость и ускорение в момент времени \(t=2\) c \[x(2)=5+2\cdot2+4\cdot2^2=25\mbox{ м}\] \[\upsilon_x(2)=2+8\cdot2=18\mbox{ м/c}\] \[a_x(2)=8\mbox{ м/c$^2$}\]
2 способ:
Проба пера
При прямолинейном движении зависимость координаты тела \(x(t)\) имеет вид: \(x(t)=5+2t+4t^2\). Найдите координату, скорость и ускорение в момент времени \(t=2\) c при таком движении?
1 способ:
Проекция скорости — это производная соответствующей координаты по времени, проекция ускорения — это производная скорости по времени: \[\upsilon_x=x'(t)=(5+2t+4t^2)'=2+8t\] \[a_x=\upsilon_x'(t)=(2+8t)'=8\] Зная зависимость скорости и ускорения от времени, найдем координату, скорость и ускорение в момент времени \(t=2\) c \[x(2)=5+2\cdot2+4\cdot2^2=25\mbox{ м}\] \[\upsilon_x(2)=2+8\cdot2=18\mbox{ м/c}\] \[a_x(2)=8\mbox{ м/c$^2$}\]
2 способ:
Данная зависимость координаты от времени совпадает с зависимостью координаты от времени при равноускоренном движении: \(\displaystyle x(t)=x_0+\upsilon_{0x}t+\frac {a_xt^2}{2}\)
Сравнивая с выражением, данным в условии, получаем: \[x_0=5\mbox{ м}\quad\upsilon_{0x}=2\mbox{ м/с}\quad a_x=8\mbox{ м/с$^2$}\] \[x(2)=x_0+\upsilon_{0x}t+\frac {a_xt^2}{2}=5+2\cdot2+4\cdot2^2=25\mbox{ м}\] \[\upsilon_x(2)=\upsilon_{0x}+a_xt=2+8\cdot2=18\mbox{ м/c}\]
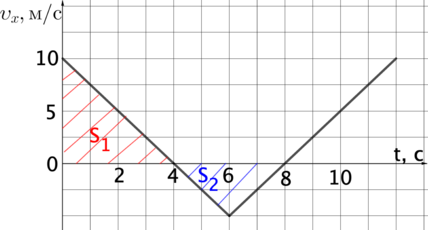
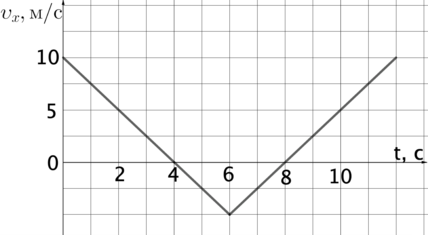
Тело движется по оси Ох. По графику зависимости проекции скорости тела \(\upsilon _x\) от времени t установите, какой путь прошло тело за время от \(t_1 = 0\) до \(t_2 = 8\) с. Чему равно премещение за этот промежуток времени? (Ответ дайте в метрах.)
 1 способ:
1 способ:
Путь — величина строго положительная, это длина пройденного телом участка траектории. Под перемещением же тела понимается изменение его координаты, перемещение может быть отрицательным. Путь можно найти как площадь под графиком зависимости скорости от времени без учета знаков, а перемещение с их учетом.
\(S_1=\frac12\cdot10\cdot4=20\) м \(S_2=\frac12\cdot(8-4)\cdot5=10\) м
Тогда путь \(L=S_1+S_2=20+10=30\) м. Перемещение равно \(S_x=S_1-S_2=20-10=10\) м. (Вторая площадь берется со знаком минус, так как находится ниже оси времени)
2 способ:
Рассмотрим три участка движения: от 0 до 4 с, от 4 с до 6 с, от 6 с до 8 с.
\(\upsilon_{0x}=10\) м/с,\(\upsilon_{1x}=0\) м/с, \(\upsilon_{2x}=-5\) м/с, \(\upsilon_{3x}=0\) м/с
\(\displaystyle a_{1x}=\frac{\upsilon_{1x}-\upsilon_{0x}}{\Delta t}=\frac{0-10}{4}=-2,5\) м/с\(^2\),\(\displaystyle a_{2x}=\frac{\upsilon_{2x}-\upsilon_{1x}}{\Delta t}=\frac{-5-(0)}{6-4}=-2,5\) м/с\(^2\)
\(\displaystyle a_{3x}=\frac{\upsilon_{3x}-\upsilon_{1x}}{\Delta t}=\frac{0-(-5)}{8-6}=2,5\) м/с\(^2\)
Тогда \(\displaystyle S_{1x}=\upsilon_{0x}t+\frac {a_{1x}t^2}{2}=10\cdot4-\frac {2,5\cdot4^2}{2}=20\) м
\(\displaystyle S_{2x}=\upsilon_{1x}t+\frac {a_{2x}t^2}{2}=0-\frac {2,5\cdot2^2}{2}=-5\) м
\(\displaystyle S_{3x}=\upsilon_{2x}t+\frac {a_{3x}t^2}{2}=-5\cdot2+\frac {2,5\cdot2^2}{2}=-5\) м
Путь \(L=|S_{1x}|+|S_{2x}|+|S_{3x}|=20+5+5=30\) м
Перемещение \(S_x=S_{1x}+S_{2x}+S_{3x}=20-5-5=10\) м


