Тема Окружность

01 Вписанные и центральные углы

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела окружность

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#133934

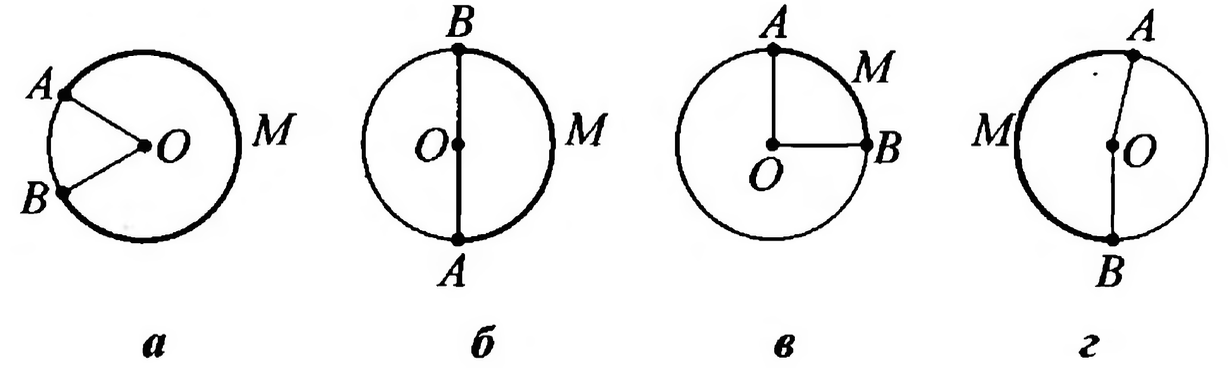
Сравните выделенные дуги с полуокружностью и укажите те из них, для которых $∪AMB = 360∘− ∠AOB$

$PIC$

Источники: Геометрия. 8 класс. Тесты: В 2 ч. Белицкая Оксана Викторовна (см. go.11klasov.net)

Показать ответ и решение

Условию $∪AMB = 360∘− ∠AOB$ удовлетворяют варианты, где дуга $AMB$ больше полуокружности. Это случаи а) и г).

Ответ: а, г

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#133938

Если центральный угол $AOB$ окружности с центром в точке $O$ и радиусом $r$ равен $90∘,$ то хорда $AB$ равна:

$1) r$

$2 2) r$

$√- 3) r$

$√ - 4) r 2$

Источники: Геометрия. 8 класс. Тесты: В 2 ч. Белицкая Оксана Викторовна (см. go.11klasov.net)

Показать ответ и решение

Рассмотрим треугольник $AOB,$ где $OA = OB = r$ (радиусы), а угол $AOB =90∘.$ Тогда $AB$ является гипотенузой прямоугольного треугольника. По теореме Пифагора:

2 2 2 2 2 2 AB = OA +OB = r +r = 2r

√ -2- √- AB = 2r =r 2

Ответ: 4)

Ошибка.
Попробуйте повторить позже

Задача 3#133940

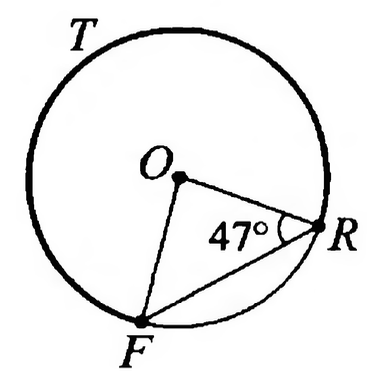
Найдите градусную меру дуги $RT F.$

$PIC$

Источники: Геометрия. 8 класс. Тесты: В 2 ч. Белицкая Оксана Викторовна (см. go.11klasov.net)

Показать ответ и решение

Треугольник $OF R$ равнобедренный, $OR = OF =r, ∠ORF = OF R= 47∘,$

$∘ ∘ ∘ ∘ ∠O= 180 − 47 − 47 =86$ Угол $FOR −$ центральный, значит, он равен $F R,$ тогда дуга $∘ ∘ ∘ FT R= 360 − 86 = 274 .$

Ответ: 274 градуса

Ошибка.
Попробуйте повторить позже

Задача 4#133941

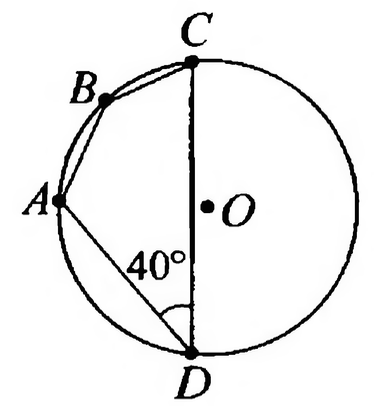
Найдите градусную меру $∠ABC.$

$PIC$

Источники: Геометрия. 8 класс. Тесты: В 2 ч. Белицкая Оксана Викторовна (см. go.11klasov.net)

Показать ответ и решение

Угол $ADC −$ вписанный, значит дуга $ABC,$ на которую он опирается равна $40∘⋅2 =80∘.$ Тогда дуга $ADC$ равна $360∘− 80∘ =280∘.$ Угол $ABC$ тоже вписанный, значит дуга $ADC,$ на которую он опирается, равна: $∘ ∘ 280 :2= 140 .$

Ответ: 140 градусов

Ошибка.
Попробуйте повторить позже

Задача 5#133944

Найдите радиус окружности, изображенной на рисунке.

$√ -- 1) 2 17$

$2) 17$

$√-- 3) 17$

$4) 34$

$PIC$

Источники: Геометрия. 8 класс. Тесты: В 2 ч. Белицкая Оксана Викторовна (см. go.11klasov.net)

Показать ответ и решение

Из прямоугольного треугольника $ABC :$

∘ --------- √----- √-- √ -- AB = AC2+ BC2 = 64+ 4= 68= 2 17

Тогда радиус окружности равен $2√17:2 =√17-$

Ответ: 3)

Ошибка.
Попробуйте повторить позже

Задача 6#133946

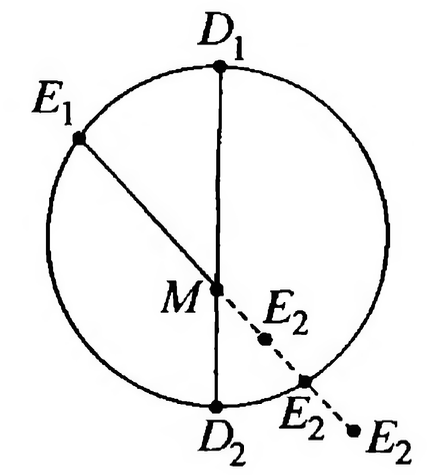
$D D − 1 1$ диаметр окружности. Известны длины отрезков:

$D1M = 24$ см, $D2M = 12$ см, $E1M =18$ см, $E2M =15$ см. Определите, где находится точка $E2.$

$PIC$

Источники: Геометрия. 8 класс. Тесты: В 2 ч. Белицкая Оксана Викторовна (см. go.11klasov.net)

Показать ответ и решение

Для определения положения точки $E 2$ относительно окружности, воспользуемся теоремой о секущих и касательных.

Если из точки $M$ проведены две секущие к окружности, то произведение длин отрезков одной секущей равно произведению длин отрезков другой секущей.

В нашем случае, секущая $D1D2$ пересекает окружность в точках $D1$ и $D2,$ а секущая $E1E2$ пересекает окружность в точках $E1$ и некоторой точке, которую мы обозначим $′ E 2.$

Тогда по теореме о секущих имеем:

D1M ⋅D2M = E1M ⋅E′2M

Подставим известные значения:

′ ′ 24⋅12= 18⋅ME 2 ⇒ ME2 =16

Так как $ME = 15 2$ см, а $ME ′= 16 2$ см, и $ME < ME′, 2 2$ то точка $E 2$ находится внутри окружности.

Ответ: Точка E2 находится внутри окружности

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#133952

По данным рисунка найдите длины хорд $A A 1 2$ и $B B . 1 2$ Единицы измерения отрезков даны в дм.

$PIC$

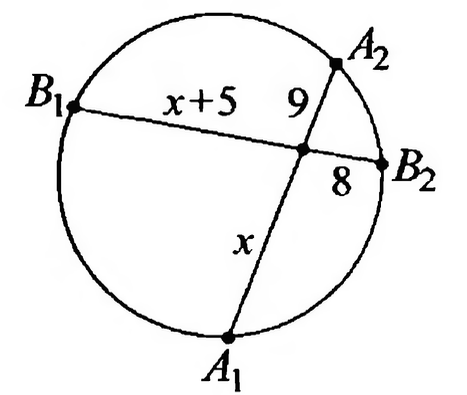
Источники: Геометрия. 8 класс. Тесты: В 2 ч. Белицкая Оксана Викторовна (см. go.11klasov.net)

Показать ответ и решение

По теореме о пересекающихся хордах окружности:

8(x+ 5)= 9x

8x+ 40 =9x

x= 40

Тогда:

A1A2 =9+ 40= 49 дм

B1B2 = 40+5 +8= 53 дм

Ответ: 49 дм и 53 дм

Ошибка.
Попробуйте повторить позже

Задача 8#133953

$∪AB = 80∘; ∪CD =44∘.$ Найдите вертикальные углы $1, 2, 3, 4.$

$PIC$

$1)∠1= 60∘; ∠2= 120∘; ∠3 =64∘; ∠4= 116∘.$

$2)∠1= 62∘; ∠2= 118∘; ∠3 =62∘; ∠4= 118∘.$

$3)∠1= 62∘; ∠2= 118∘; ∠3 =118∘; ∠4= 62∘.$

$4)∠1= 90∘; ∠2= 180∘; ∠3 =90∘; ∠4= 180∘.$

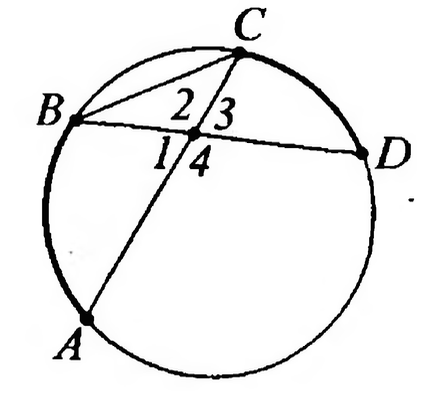
Источники: Геометрия. 8 класс. Тесты: В 2 ч. Белицкая Оксана Викторовна (см. go.11klasov.net)

Показать ответ и решение

$∠CBD =22∘,$ так как он вписанный и опирается на дугу $CD,$ равную $44∘.∠BCA = 40∘$ так как он вписанный и опирается на дугу $BA,$ равную $∘ 80.$ Тогда $∘ ∘ ∘ ∘ ∠2 = 180 − (40 + 22)= 118.$ Угол $4$ также равен $∘ 118.$ Тогда углы $1$ и $3$ равны по $∘ ∘ ∘ 180 − 118 = 62.$

Ответ: 2)

Ошибка.
Попробуйте повторить позже

Задача 9#133957

Какое утверждение верно для центрального угла окружности?

Источники: Авторская, Хаткова Р. Р.

Показать ответ и решение

По определению центрального угла:

Центральный угол измеряется дугой, на которую он опирается
Это фундаментальное свойство, следующее из определения градусной меры угла
Вариант о половине дуги описывает свойство вписанного угла
Остальные варианты не соответствуют свойствам центральных углов

Ответ: Он равен дуге, на которую опирается

Ошибка.
Попробуйте повторить позже

Задача 10#133958

Если два вписанных угла опираются на одну и ту же дугу, то:

Источники: Авторская, Хаткова Р. Р.

Показать ответ и решение

Ключевое свойство вписанных углов гласит, что все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой. Это потому, что каждый такой угол измеряется половиной соответствующей дуги.

Ответ: Они равны между собой