Поиск точек экстремума у элементарных функций —Каталог задач по ЕГЭ - Математика

Ошибка.
Попробуйте повторить позже

Задача 1#17139

Найдите точку минимума функции $y = x3− 8,5x2+ 10x− 13.$

Источники: Сборник И.В. Ященко 2025 г. Вариант 36

Показать ответ и решение

Обозначим $f(x) = x3− 8,5x2+ 10x − 13.$

1.: Найдем производную функции: $f′(x)= 3x2− 17x+ 10.$
2.: Нули производной: $2 x= 3$ и $x= 5.$
3.: Применим метод интервалов для определения знаков производной. В каждом из нулей знак производной меняется на противоположный.

$PIC$
4.: Теперь можем нарисовать эскиз графика. На промежуткe $( ) 2;5 3$ производная отрицательна, то есть исходная функция убывает. На оставшихся промежутках производная положительна и функция возрастает.

$PIC$

На полученном эскизе видно, что точкой минимума является $x= 5,$ так как левее нее функция убывает, а правее — возрастает.

Ответ: 5

Ошибка.
Попробуйте повторить позже

Задача 2#2081

Найдите точку максимума функции $y = − x2$ .

Показать ответ и решение

ОДЗ: $x$ – произвольный.

1)

y′ = − 2x

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна $0$ или не существует):

− 2x = 0 ⇔ x = 0.

Производная существует при любом $x$ .

2) Найдём промежутки знакопостоянства $y′$ :

$PIC$

3) Эскиз графика:

$PIC$

Таким образом, $x = 0$ – точка максимума функции $y$ .

Ответ: 0

Ошибка.
Попробуйте повторить позже

Задача 3#2082

Найдите точку минимума функции $y = x2 + 2x + 2$ на отрезке $[− 2;2]$ .

Показать ответ и решение

ОДЗ: $x$ – произвольный.

1)

y′ = 2x + 2

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна $0$ или не существует):

2x + 2 = 0 ⇔ x = − 1.

Производная существует при любом $x$ .

2) Найдём промежутки знакопостоянства $y′$ :

$PIC$

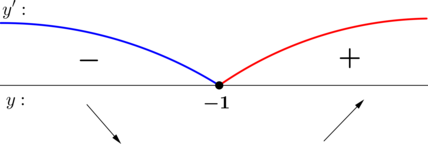
3) Найдём промежутки знакопостоянства $′ y$ на рассматриваемом отрезке $[− 2;2]$ :

$PIC$

4) Эскиз графика на отрезке $[− 2;2]$ :

$PIC$

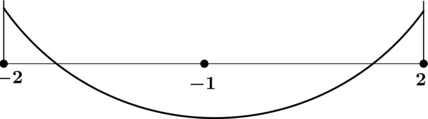
Таким образом, $x = − 1$ – точка минимума функции $y$ на $[− 2;2]$ .

Ответ: -1

Ошибка.
Попробуйте повторить позже

Задача 4#2191

Найдите точку локального минимума функции $y = x3 − 3x$ .

Показать ответ и решение

ОДЗ: $x$ – произвольный.

1)

y′ = 3x2 − 3

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна $0$ или не существует):

2 3x − 3 = 0 ⇔ x = ±1.

Производная существует при любом $x$ .

2) Найдём промежутки знакопостоянства $y′$ :

$PIC$

3) Эскиз графика $y$ :

$PIC$

Таким образом, $x = 1$ – точка локального минимума функции $y$ .

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 5#13551

Найдите точку минимума функции $y = 2x− ln(x+ 11)+ 8.$

Показать ответ и решение

Обозначим $f(x) = 2x − ln(x+ 11)+8.$

Найдем производную функции:

f′(x)= (2x− ln(x+ 11)+ 8)′ = ′ ′ ′ = (2x)− (ln(x+ 11) +(8) = --1-- --1-- 2x-+-21 = 2− x+ 11 + 0 =2 − x+ 11 = x+ 11

Легко видеть, что полученная дробь зануляется при $−21 x= -2--$ и не определена при $x= −11.$

Применим метод интервалов для определения знаков производной. Обе критические точки встречаются в нечетном числе множителей, следовательно, знак в них будет меняться.

$PIC$

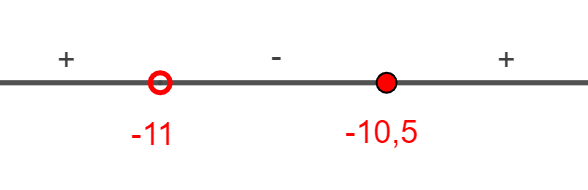
В точке минимума функции её производная обнуляется и меняет знак с « $−$ » на « $+$ », так как до точки минимума функция убывала, а после — начала возрастать. Значит, $x =− 10,5$ — точка минимума функции $y = 2x − ln(x+ 11)+8.$

Ответ: -10,5

Ошибка.
Попробуйте повторить позже

Задача 6#16753

Найдите точку минимума функции $y = 2x− ln(x− 3)+ 5.$

Показать ответ и решение

Заметим, что данная функция определена при $x> 3,$ поэтому далее будем рассматривать ее на промежутке $(3;+∞ ).$

Найдем критические точки заданной функции

f(x) =2x − ln(x− 3)+5

Для этого вычислим её производную:

f′(x)= (2x)′− (ln(x − 3))′+5′ = 1 2x − 7 = 2 − x−-3 + 0=-x−-3

Далее найдем нули производной:

f′(x)= 0 ⇒ 2x−-7 = 0 x− 3 2x − 7 = 0 ⇒ x= 3,5

Единственная критическая точка — это $x= 3,5,$ в этой точке производная меняет знак. Для того чтобы определить, является ли $x= 3,5$ точкой минимума, нужно определить знаки производной при $x< 3,5$ и $x> 3,5.$

Если $x > 3,5,$ то $f′(x)> 0,$ если $x < 3,5,$ то $f′(x)< 0.$ Значит, точка $x= 3,5$ является точкой минимума, так как в ней производная меняет знак с « $−$ » на « $+$ » при проходе слева направо.

Ответ: 3,5

Ошибка.
Попробуйте повторить позже

Задача 7#17243

Найдите точку максимума функции $x3 y = 14 +x − 3 .$

Показать ответ и решение

Обозначим $x3 f(x) = 14 +x − 3 .$

1.

Найдем производную функции:

′ 2 f (x)= 1 − x

2.

Нули производной $x = ±1.$

3.

Применим метод интервалов для определения знаков производной. В каждом из нулей знак производной меняется на противоположный.

$PIC$

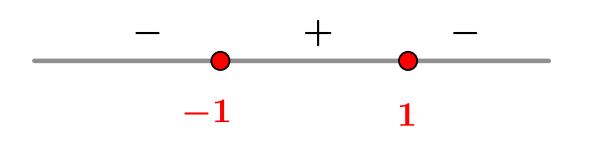
4.

Теперь можем нарисовать эскиз графика. На промежуткe $(− 1;1)$ производная положительна, то есть исходная функция возрастает. Левее точки $x= − 1$ и правее точки $x =1$ производная отрицательна и функция убывает.

$PIC$

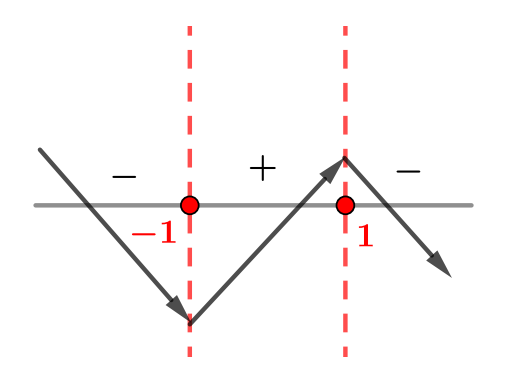
На полученном эскизе видно, что точкой максимума является $x= 1,$ так как левее нее функция возрастает, а правее — убывает.

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 8#19493

Найдите точку максимума функции $3 y =x − 108x+ 115.$

Показать ответ и решение

Найдем критические точки заданной функции. Для этого вычислим ее производную:

′ ( 3 )′ ( f)(x′) = x − 108x+ 115 = = x3 − (108x)′+ (115)′ = 3x2− 108

Далее найдем нули производной:

′ 2 f (x)= 0 ⇔ 3x − 108 = 0 x2 = 36 ⇔ x= ±6

Так как производная непрерывна, то имеем промежутки знакопостоянства производной:

(−∞; −6), (− 6;6), (6;+∞ )

Тогда при $x∈ (−∞; −6)$ производная $f′(x)> 0,$ при $x∈ (−6;6)$ производная $f′(x)< 0,$ а при $x∈ (6;+ ∞ )$ производная $f′(x) > 0.$

Значит, на промежутках $(− ∞;− 6)$ и $(6;+ ∞)$ функция возрастает, а на промежутке $(−6;6)$ — убывает.

Точка $x0$ является точкой максимума, если в ней производная меняет знак с « $+$ » на « $−$ » при движении слева направо. Следовательно, $x = −6$ — точка максимума.

Ответ: -6

Ошибка.
Попробуйте повторить позже

Задача 9#32244

Найдите точку минимума функции $3 2 y = x + 5x + 7x − 5.$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

y′ = 3x2+ 10x +7

Найдем нули производной:

y′ = 0 2 3x + 10x+ 7= 0 x= −1;− 7 3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x =− 1$ является точкой минимума.

Ответ: -1

Ошибка.
Попробуйте повторить позже

Задача 10#32245

Найдите точку максимума функции $y = 7+ 12x − x3.$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y= 12− 3x

Найдем нули производной:

′ 2 y= 0 ⇒ x = 4 ⇔ x =±2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= 2$ является точкой максимума.

Ответ: 2

Ошибка.
Попробуйте повторить позже

Задача 11#32246

Найдите точку минимума функции $y = 7+ 12x− x3.$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y= 12− 3x

Найдем нули производной:

′ 2 y= 0 ⇒ x = 4 ⇔ x =±2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= −2$ является точкой минимума.

Ответ: -2

Ошибка.
Попробуйте повторить позже

Задача 12#32247

Найдите точку максимума функции $y = 9x2− x3.$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 18x − 3x

Найдем нули производной:

′ y = 0 ⇒ 3x(6 − x)= 0 ⇔ x= 0;6

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= 6$ является точкой максимума.

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 13#32248

Найдите точку минимума функции $y = 9x2− x3.$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 18x − 3x

Найдем нули производной:

′ y = 0 ⇒ 3x(6 − x)= 0 ⇔ x= 0;6

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= 0$ является точкой минимума.

Ответ: 0

Ошибка.
Попробуйте повторить позже

Задача 14#32249

Найдите точку максимума функции $y = x3− 9x− 7. 3$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = x − 9

Найдем нули производной:

′ 2 y= 0 ⇒ x = 9 ⇔ x =±3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= −3$ является точкой максимума.

Ответ: -3

Ошибка.
Попробуйте повторить позже

Задача 15#32250

Найдите точку минимума функции $y = x3 − 9x− 7. 3$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = x − 9

Найдем нули производной:

′ 2 y= 0 ⇒ x = 9 ⇔ x =±3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= 3$ является точкой минимума.

Ответ: 3

Ошибка.
Попробуйте повторить позже

Задача 16#32251

Найдите точку максимума функции $y = 5+ 9x − x3. 3$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 9− x

Найдем нули производной:

′ 2 y= 0 ⇒ x = 9 ⇔ x =±3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= 3$ является точкой максимума.

Ответ: 3

Ошибка.
Попробуйте повторить позже

Задача 17#32252

Найдите точку минимума функции $y = 5+ 9x− x3. 3$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 9− x

Найдем нули производной:

′ 2 y= 0 ⇒ x = 9 ⇔ x =±3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= −3$ является точкой минимума.

Ответ: -3

Ошибка.
Попробуйте повторить позже

Задача 18#32262

Найдите точку минимума функции $y = −21x2− x3+32.$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y= −42x− 3x

Найдем нули производной:

′ y =0 ⇒ −3x(x+ 14)= 0 ⇔ x= −14;0

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= −14$ является точкой минимума.

Ответ: -14

Ошибка.
Попробуйте повторить позже

Задача 19#32236

Найдите точку максимума функции $y = x3− 48x+ 17.$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y= 3x − 48

Найдем нули производной:

′ 2 y = 0 ⇒ x = 16 ⇔ x= ±4

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= −4$ является точкой максимума.

Ответ: -4

Ошибка.
Попробуйте повторить позже

Задача 20#32237

Найдите точку максимума функции $y = x3− 3x2+ 2$ .

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y= 3x − 6x

Найдем нули производной:

′ y = 0 ⇒ 3x(x − 2)= 0 ⇔ x= 0;2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

Следовательно, $x= 0$ является точкой максимума.

Ответ: 0

12.01 Поиск точек экстремума у элементарных функций