.00 №16 из ЕГЭ 2017
Ошибка.
Попробуйте повторить позже
Страховой фонд владеет акциями, стоимость которых равна тыс. рублей в конце каждого года с номером
где
Фонд может продать все акции в конце некоторого года и положить все вырученные с продажи средства на счет в банке. Известно,
что тогда в конце каждого следующего года банк будет увеличивать сумму, находящую на счете, в
раз, где
— некоторое
положительное большее единицы число. Оказалось, что если фонд продаст все акции и вложит деньги в банк именно в конце 21-ого
года, то в конце 25-ого года он получит наибольшую из возможных прибыль. Определите, какие при этом значения может
принимать число
Источники:
Если фонд продаст акции в конце -ого года, то на конец 25-ого года они пролежат в банке
лет. Так как каждый год банк
увеличивает сумму в
раз, то за
лет он увеличит ее в
раз. Следовательно, на конец 25-ого года фонд будет иметь
сумму в тыс. рублей, равную
Рассмотрим эту функцию. В ней — некоторое конкретное, но неизвестное число, а
— переменная. Найдем ее
производную:
Таким образом, нулем производной, учитывая, что является
Причем заметим, что эта точка является точкой максимума. Следовательно, до функция возрастает, а после —
убывает.
Таким образом, если, продав акции в 21-ый год, фонд получит наибольшую из возможных прибыль, то это значит, что мы имеем такой график:
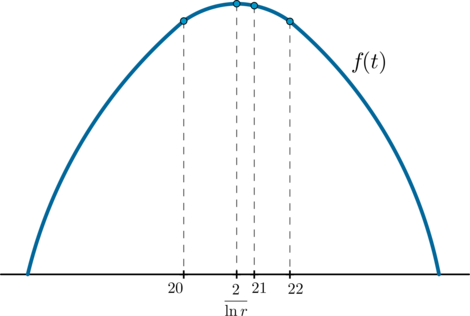
Для примера на картинке точка находится правее точки максимума. Может быть наоборот: 21 будет находиться
левее точки максимума. Главное, что точка графика с абсциссой 21 выше, чем точки графика с абсциссами 20 или
22!
Тогда и
Из этого условия будет следовать, что
при любом целом
от 1 до 25.
Решим полученную систему:
Отсюда получаем, что
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




