17.01 Задачи №17 из ЕГЭ прошлых лет
Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. При этом
— точка пересечения
его диагоналей
и
Известно, что
— параллелограмм.
а) Докажите, что две стороны пятиугольника равны.
б) Найдите , если известно, что
Источники:
а) Так как — параллелограмм, то
и
Тогда
— трапеция, так как
и
Вокруг трапеции описана окружность, следовательно, она
равнобедренная, в которой
Значит, в пятиугольнике равны стороны
и
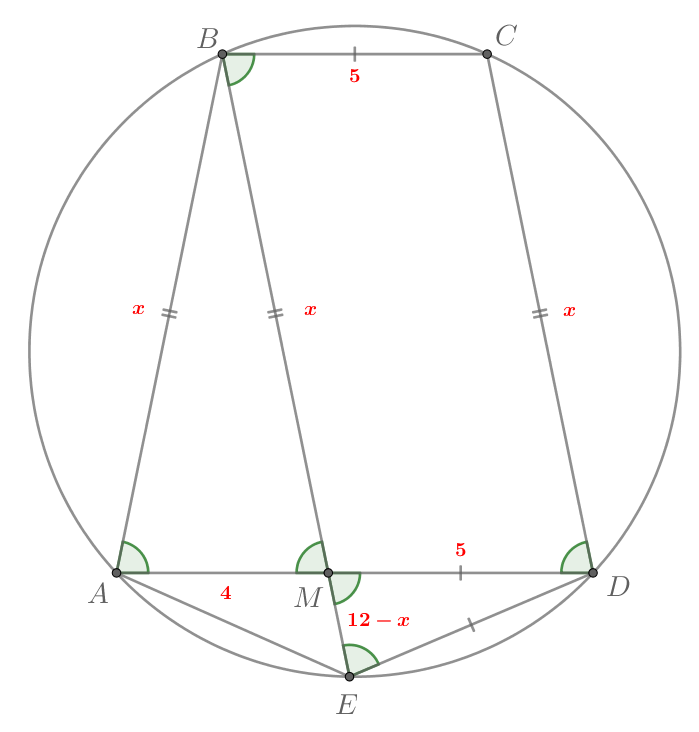
б) Аналогично пункту а) получаем, что — равнобедренная трапеция, в
которой
и
Так как по условию — параллелограмм, то
Тогда
Пусть По свойству пересекающихся хорд
и
в
окружности:
Заметим, что если то
Тогда в
стороны будут
равны 5, 5 и 10, что невозможно по неравенству треугольника.
Значит,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. Известно, что
а) Докажите, что
б) Найдите длину диагонали если
Источники:
а) Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Пусть — точка пересечения диагоналей
и
Тогда в
четырехугольнике
известно, что
и
значит,
— параллелограмм. Следовательно,
и
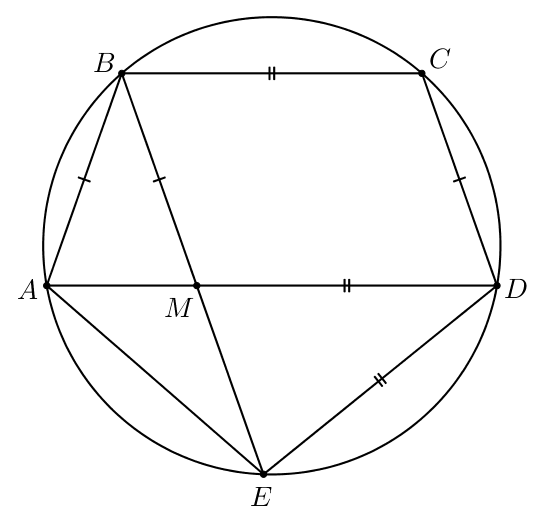
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
Таким образом,
б) В пункте а) мы узнали, что значит,
Тогда по свойству пересекающихся хорд и
в окружности:
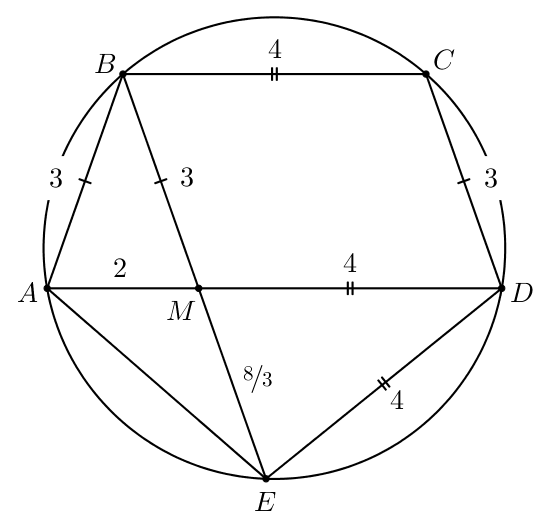
Значит,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. Известно, что
а) Докажите, что
б) Найдите длину диагонали если
Источники:
а) Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Пусть
— точка пересечения диагоналей
и
Тогда в четырехугольнике
известно, что
и
значит,
— параллелограмм. Следовательно,
и
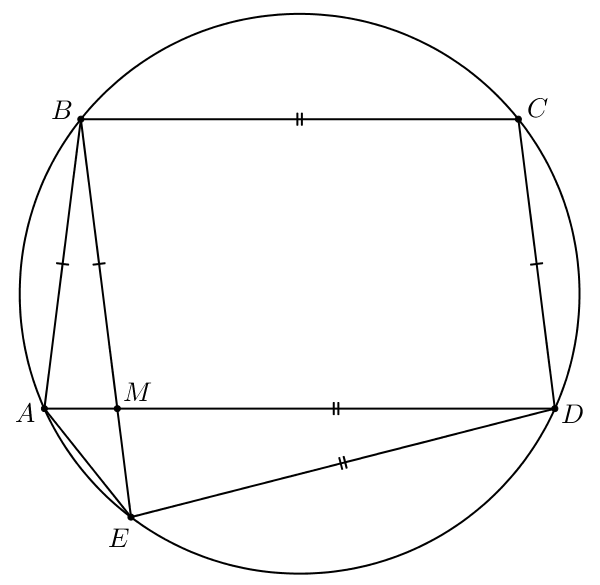
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
Таким образом,
б) В пункте а) мы узнали, что значит,
Тогда по свойству пересекающихся хорд и
в окружности:
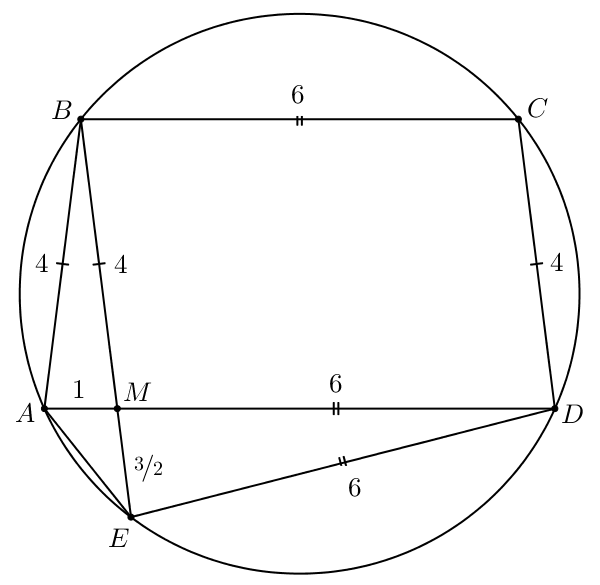
Значит,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. Известно, что
а) Докажите, что
б) Найдите длину диагонали если
Источники:
а) Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Пусть — точка пересечения диагоналей
и
Тогда в
четырехугольнике
известно, что
и
значит,
— параллелограмм. Следовательно,
и
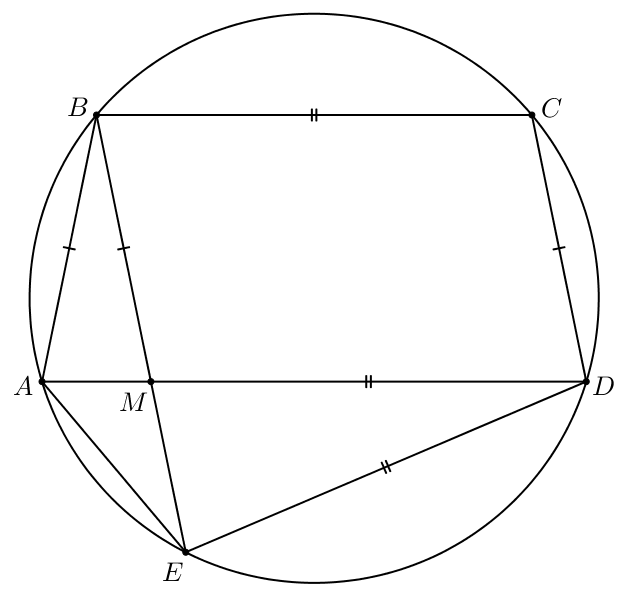
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
Таким образом,
б) В пункте а) мы узнали, что значит,
Тогда по свойству пересекающихся хорд и
в окружности:

Значит,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
а) Докажите, что прямая параллельна биссектрисе угла
б) Найдите если
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Заметим, что как отрезки касательных, проведенных к
окружности из одной точки, а значит, треугольник
— равнобедренный.
Поэтому его биссектриса из вершины
также является и высотой, то есть
При этом как опирающийся на диаметр, а значит,
Таким образом,
и
следовательно,

б) Рассмотрим четырехугольник В нем
так
как радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Рассмотрим треугольники и
В них
и
Значит,
по двум углам. Запишем отношение
подобия:
По теореме Пифагора для прямоугольного треугольника
Тогда так как — центр окружности, то
Таким образом,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
а) Докажите, что прямая параллельна биссектрисе угла
б) Найдите если
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Заметим, что как отрезки касательных, проведенных к
окружности из одной точки, а значит, треугольник
— равнобедренный.
Поэтому его биссектриса из вершины
также является и высотой, то есть
При этом как опирающийся на диаметр, а значит,
Таким образом,
и
следовательно,

б) Рассмотрим четырехугольник В нем
так
как радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Рассмотрим треугольники и
В них
и
Значит,
по двум углам. Запишем отношение
подобия:
По теореме Пифагора для прямоугольного треугольника
Тогда так как — центр окружности, то
Таким образом,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
а) Докажите, что прямая параллельна биссектрисе угла
б) Найдите если
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Заметим, что как отрезки касательных, проведенных к
окружности из одной точки, а значит, треугольник
— равнобедренный.
Поэтому его биссектриса из вершины
также является и высотой, то есть
При этом как опирающийся на диаметр, а значит,
Таким образом,
и
следовательно,

б) Рассмотрим четырехугольник В нем
так
как радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Рассмотрим треугольники и
В них
и
Значит,
по двум углам. Запишем отношение
подобия:
По теореме Пифагора для прямоугольного треугольника
Тогда так как — центр окружности, то
Таким образом,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
a) Докажите, что
б) Найдите расстояние от точки до прямой
если известно, что
и
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Рассмотрим четырехугольник В нем
так как
радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Таким образом,

б) В прямоугольном треугольнике имеем:
Пусть — точка пересечения
и
Заметим, что
как отрезки касательных, проведенных к окружности из одной точки, а
значит, треугольник
— равнобедренный. Поэтому его биссектриса из
вершины
также является высотой и медианой, то есть
и
Тогда в прямоугольном треугольнике имеем:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
a) Докажите, что
б) Найдите расстояние от точки до прямой
если известно, что
и
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Рассмотрим четырехугольник В нем
так как
радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Таким образом,

б) В прямоугольном треугольнике имеем:
Пусть — точка пересечения
и
Заметим, что
как отрезки касательных, проведенных к окружности из одной точки, а
значит, треугольник
— равнобедренный. Поэтому его биссектриса из
вершины
также является высотой и медианой, то есть
и
Тогда в прямоугольном треугольнике имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается сторон угла с вершиной
в точках
и
Отрезок
— диаметр этой окружности.
a) Докажите, что
б) Найдите расстояние от точки до прямой
если известно, что
и
Источники:
а) Центр окружности, вписанной в угол, лежит на его биссектрисе, так как он
равноудален от сторон этого угла. Тогда — биссектриса угла
Также
центр
лежит на диаметре
Рассмотрим четырехугольник В нем
так как
радиусы
и
проведенные в точку касания, перпендикулярны
касательным
и
соответственно. Значит, сумма противоположных углов
четырехугольника
равна
следовательно,
— вписанный.
Тогда
как углы, опирающиеся на одну дугу описанной около
этого четырехугольника окружности.
Таким образом,

б) В прямоугольном треугольнике имеем:
Пусть — точка пересечения
и
Заметим, что
как отрезки касательных, проведенных к окружности из одной точки, а
значит, треугольник
— равнобедренный. Поэтому его биссектриса из
вершины
также является высотой и медианой, то есть
и
Тогда в прямоугольном треугольнике имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Периметр треугольника равен 36. Точки
и
— середины сторон
и
соответственно. Отрезок
касается окружности, вписанной в треугольник
а) Докажите, что
б) Найдите площадь треугольника если
Источники:
а) Пусть
и
По условию
— середина
поэтому
Также
— середина
поэтому
Тогда
— средняя линия треугольника
параллельная
следовательно,
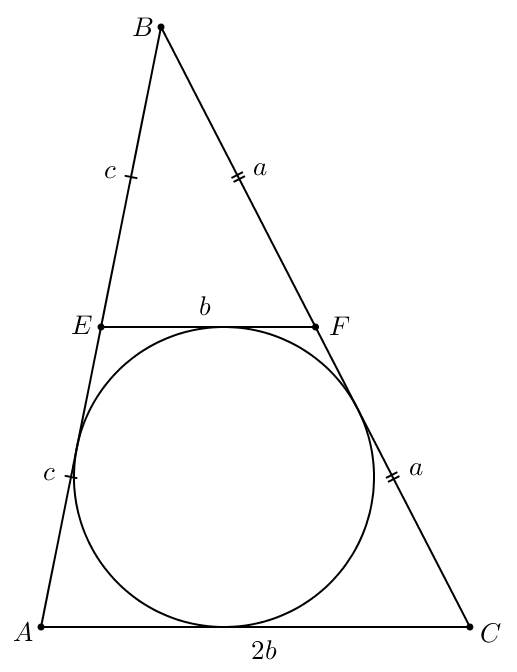
По условию периметр треугольника равен 36, значит,
С другой стороны, касается вписанной окружности треугольника
поэтому четырехугольник
— описанный, следовательно, суммы его
противоположных сторон равны:
Таким образом,
Значит,
б) По условию Тогда запишем теорему Пифагора для
В предыдущем пункте мы доказали, что
Следовательно,
Имеем систему уравнений:

Тогда можем найти площадь прямоугольного треугольника
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Периметр треугольника равен 24. Точки
и
— середины сторон
и
соответственно. Отрезок
касается окружности, вписанной в треугольник
а) Докажите, что
б) Найдите площадь треугольника если
Источники:
а) Пусть
и
По условию
— середина
поэтому
Также
— середина
поэтому
Тогда
— средняя линия треугольника
параллельная
следовательно,
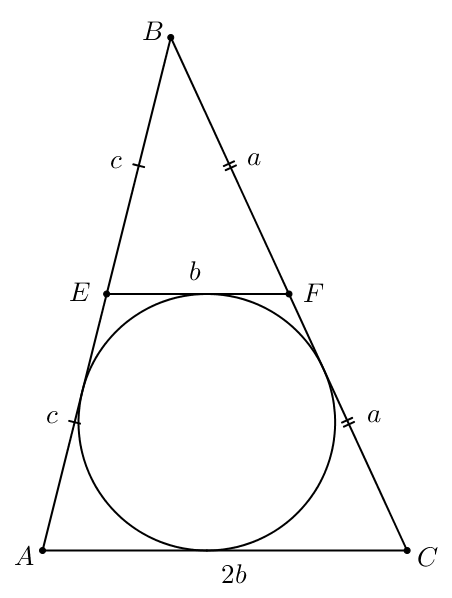
По условию периметр треугольника равен 24, значит,
С другой стороны, касается вписанной окружности треугольника
поэтому четырехугольник
— описанный, следовательно, суммы его
противоположных сторон равны:
Таким образом,
Значит,
б) По условию Тогда запишем теорему Пифагора для
В предыдущем пункте мы доказали, что
Следовательно,
Имеем систему уравнений:

Тогда можем найти площадь прямоугольного треугольника
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В треугольнике угол
равен
Окружность, вписанная в
треугольник, касается стороны
в точке
а) Докажите, что отрезок не больше утроенного радиуса вписанной в
треугольник окружности.
б) Найдите если известно, что отрезок
в 2,8 раза больше
радиуса вписанной в треугольник окружности.
Источники:
а) Пусть — центр окружности,
— точка касания со стороной
Тогда
— отрезок биссектрисы угла
— радиусы.
Следовательно,
откуда
Если
то по
неравенству треугольника
Если то
Следовательно, по итогу Что и требовалось доказать.

б) Рассмотрим
Тогда по теореме
косинусов для этого треугольника имеем
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник В нём провели высоты
и
которые пересеклись в точке
а) Докажите, что угол равен углу
б) Найдите расстояние от центра описанной окружности треугольника
до его стороны
если известно, что
а
Источники:
а) Рассмотрим четырёхугольник Заметим, что он вписанный, так как
сумма его противоположных углов равна
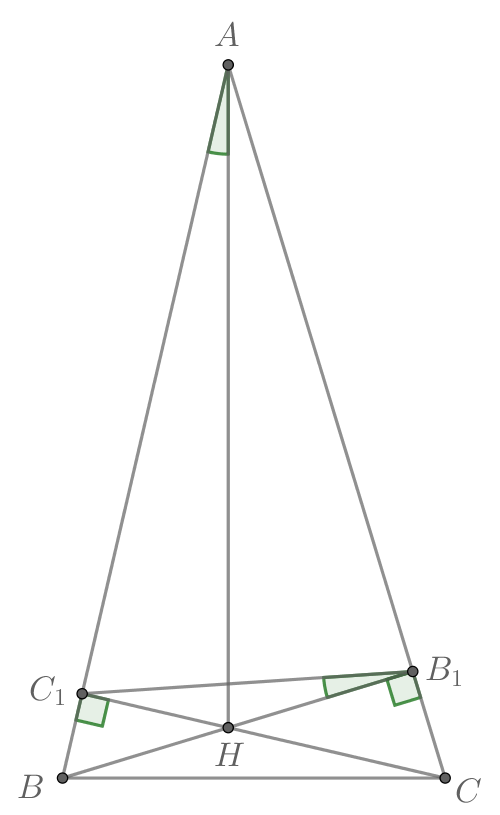
Проведем его диагонали и
Так как
— вписанный, то
углы, опирающиеся на его сторону
равны, то есть
Что и требовалось доказать.
б) Заметим, что с коэффициентом
Докажем
это.
Заметим, что четырехугольник — вписанный, так как углы,
опирающиеся на его сторону
равны
Следовательно, по свойству вписанного четырехугольника.
Угол
общий, значит,
по двум углам с коэффициентом
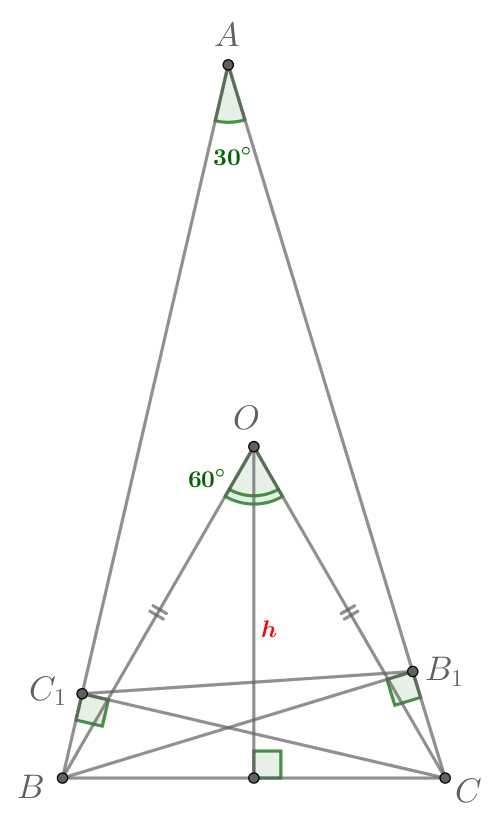
Тогда запишем отношение подобия:
Пусть — центр описанной окружности треугольника
Тогда
центральный угол
в два раза больше вписанного угла
то
есть
Значит, равносторонний, так как в нем есть угол в
и
как радиусы описанной окружности треугольника
Таким
образом,
Тогда расстояние от точки
до
равно высоте равностороннего
треугольника, то есть
б) 18
Ошибка.
Попробуйте повторить позже
Дана трапеция с боковой стороной
которая перпендикулярна
основаниям. Из точки
на сторону
опущен перпендикуляр
На
стороне
взята точка
так, что прямые
и
перпендикулярны.
a) Докажите, что прямые и
параллельны.
б) Найдите отношение к
если
Источники:
а) Пусть — меньшее основание и прямые
и
пересекаются в точке

По условию и
значит,
Тогда прямоугольные
треугольники
и
подобны по двум углам (есть общий
угол и прямой), следовательно,
Тогда имеем:
Значит, по отношению сторон и углу между ними. Тогда
б) Так как то

Заметим, что если то смежный ему
Тогда в треугольнике
Тогда в треугольнике
Следовательно, треугольник равнобедренный с основанием
Тогда
— высота и медиана, следовательно,
Значит,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана трапеция с боковой стороной
которая перпендикулярна
основаниям. Из точки
на сторону
опущен перпендикуляр
На
стороне
взята точка
так, что прямые
и
перпендикулярны.
a) Докажите, что прямые и
параллельны.
б) Найдите отношение к
если
Источники:
а) Пусть — меньшее основание и прямые
и
пересекаются в точке

По условию и
значит,
Тогда прямоугольные
треугольники
и
подобны по двум углам (есть общий
угол и прямой), следовательно,
Тогда имеем:
Значит, по отношению сторон и углу между ними. Тогда
б) Так как то

Заметим, что если то смежный ему
Тогда в треугольнике
Тогда в треугольнике
Следовательно, треугольник прямоугольный с углом
Тогда высота
делит треугольник
на два прямоугольных подобных ему
треугольника
и
Из подобия треугольников
и
имеем:
Тогда окончательно получаем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана трапеция с боковой стороной
которая перпендикулярна
основаниям. Из точки
на сторону
опущен перпендикуляр
На
стороне
взята точка
так, что прямые
и
перпендикулярны.
a) Докажите, что прямые и
параллельны.
б) Найдите отношение к
если
Источники:
а) Пусть — меньшее основание и прямые
и
пересекаются в точке

По условию и
значит,
Тогда прямоугольные
треугольники
и
подобны по двум углам (есть общий
угол и прямой), следовательно,
Тогда имеем:
Значит, по отношению сторон и углу между ними. Тогда
б) Так как то

Заметим, что если то смежный ему
Тогда в треугольнике
Тогда в треугольнике
Следовательно, треугольник прямоугольный с углом
Тогда высота
делит треугольник
на два прямоугольных подобных ему
треугольника
и
Из подобия треугольников
и
имеем:
Тогда окончательно получаем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
и
На них из
точек
и
опущены перпендикуляры
и
соответственно.
a) Докажите, что прямые и
параллельны.
б) Найдите отношение к
если
Источники:
а) Рассмотрим четырехугольник В нем имеем:
Значит, четырехугольник вписанный. Тогда
Рассмотрим четырехугольник В нем имеем:
Значит, четырехугольник вписанный. Тогда

Следовательно,
Таким образом, соответственные углы, образованные прямыми и
и
секущей
равны, поэтому
б) Пусть и
пересекаются в точке
Тогда в треугольниках
и
имеем
— общий и
по предыдущему пункту.
Тогда треугольники
и
подобны, значит,

Рассмотрим треугольник В нем имеем:
Тогда рассмотрим треугольник В нем имеем:
Так как — высота прямоугольного треугольника
то она разбивает
его на два треугольника
и
подобных ему. Тогда из подобия
треугольников
и
Тогда окончательно получаем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
и
На них из
точек
и
опущены перпендикуляры
и
соответственно.
a) Докажите, что прямые и
параллельны.
б) Найдите отношение к
если
Источники:
а) Рассмотрим четырехугольник В нем имеем:
Значит, четырехугольник вписанный. Тогда
Рассмотрим четырехугольник В нем имеем:
Значит, четырехугольник вписанный. Тогда

Следовательно,
Таким образом, соответственные углы, образованные прямыми и
и
секущей
равны, поэтому
б) Пусть и
пересекаются в точке
Тогда в треугольниках
и
имеем
— общий и
по предыдущему пункту.
Тогда треугольники
и
подобны, значит,
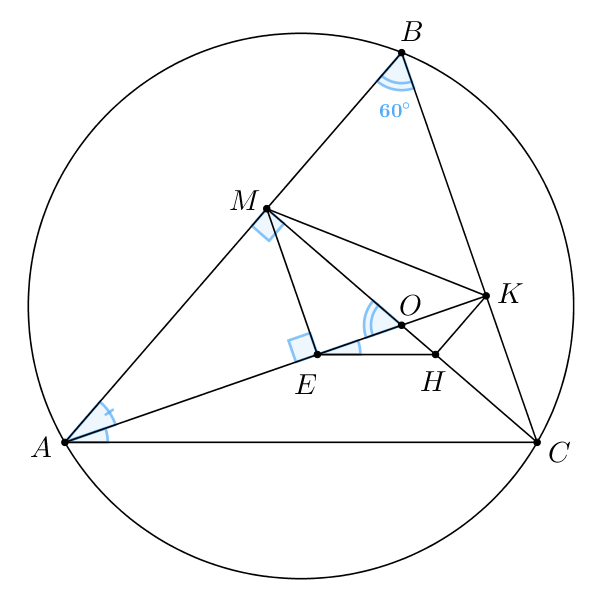
Рассмотрим треугольник В нем имеем:
Тогда рассмотрим треугольник В нем имеем:
Так как — высота прямоугольного треугольника
то она разбивает
его на два треугольника
и
подобных ему. Тогда из подобия
треугольников
и
Тогда окончательно получаем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
и
На них из
точек
и
опущены перпендикуляры
и
соответственно.
a) Докажите, что прямые и
параллельны.
б) Найдите отношение к
если
Источники:
а) Рассмотрим четырехугольник В нем имеем:
Значит, четырехугольник вписанный. Тогда
Рассмотрим четырехугольник В нем имеем:
Значит, четырехугольник вписанный. Тогда

Следовательно,
Таким образом, соответственные углы, образованные прямыми и
и
секущей
равны, поэтому
б) Пусть и
пересекаются в точке
Тогда в треугольниках
и
имеем
— общий и
по предыдущему пункту.
Тогда треугольники
и
подобны, значит,

Рассмотрим треугольник В нем имеем:
Тогда рассмотрим треугольник В нем имеем:
Так как — проведенная к основанию высота прямоугольного
равнобедренного треугольника
то она является и медианой. Тогда
значит,
Тогда окончательно получаем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



