1.02 Треугольник: высота, биссектриса, медиана
Ошибка.
Попробуйте повторить позже
В треугольнике
— высота,
Найдите
Ответ дайте в градусах.
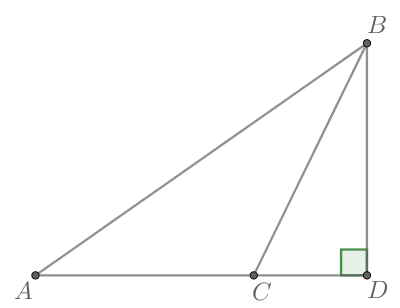
Так как — высота, то
Сумма углов треугольника равна
тогда
Так как то
При этом тогда
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса,
Найдите
Ответ дайте в градусах.
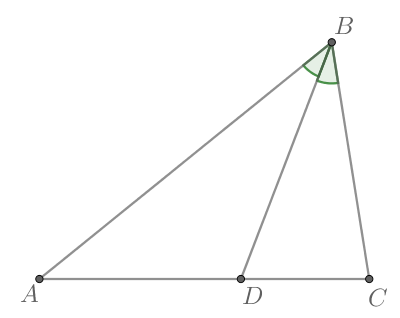
Так как — биссектриса, то
тогда имеем:
Сумма углов треугольника равна тогда получаем
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса,
Найдите
Ответ дайте в градусах.
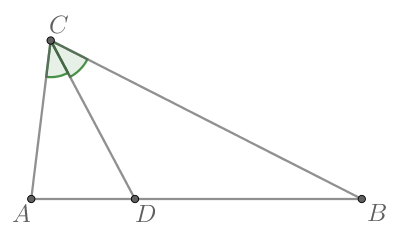
Так как — биссектриса, то
Тогда имеем:
Сумма углов треугольника равна тогда получаем
Ошибка.
Попробуйте повторить позже
В треугольнике
— биссектриса,
Найдите
Ответ дайте в градусах.
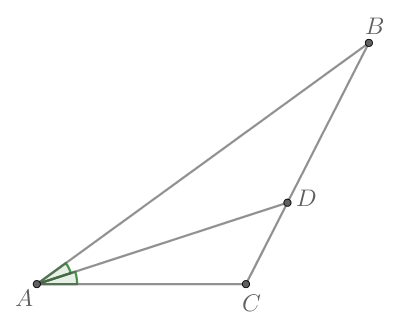
Так как — биссектриса, то
Тогда
Сумма углов треугольника равна тогда
В треугольнике
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса,
Найдите наименьший угол в треугольнике
Ответ
дайте в градусах.
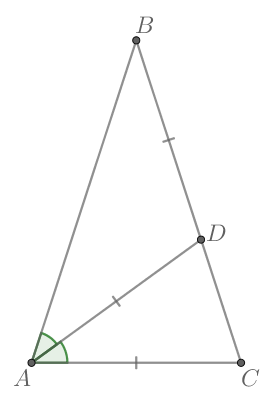
У равнобедренного треугольника углы при основании равны. Так как то
Согласно теореме о внешнем угле треугольника,
Тогда
Таким образом, — наименьший.
Так как — биссектриса, то
По теореме о сумме углов треугольника
Найдем угол
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса,
— такая точка на
что
Найдите
Ответ дайте в
градусах.
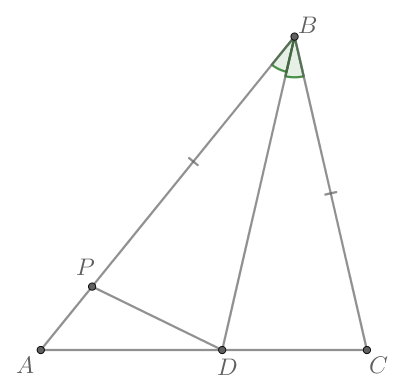
Сумма углов в треугольнике равна тогда
Так как — биссектриса, то
Треугольники и
равны по двум сторонам и углу между ними,
тогда
Тогда
Значит,
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса
внешнего угла при вершине
При этом точка
лежит на продолжении
стороны
На продолжении стороны
за точку
выбрана точка
таким образом, что
Найдите
Ответ дайте в градусах.
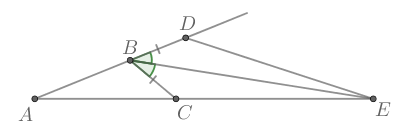
Согласно теореме о внешнем угле треугольника,
Так как — биссектриса
то имеем:
Так как сумма углов в треугольнике равна то имеем:
Треугольники и
равны по двум сторонам и углу между ними,
тогда получаем
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса,
Найдите
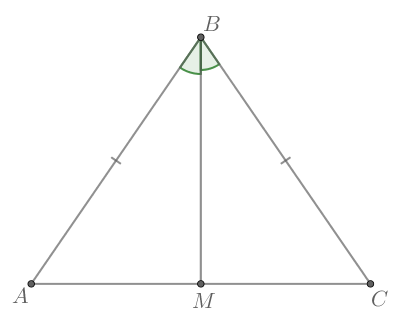
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой, тогда — медиана и
Таким образом,
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— медиана,
Найдите
Ответ дайте в градусах.
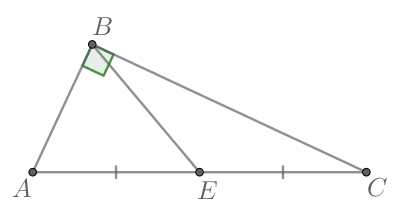
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда имеем:
Значит, треугольник — равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда
имеем:
Так как внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним, то получаем
Ошибка.
Попробуйте повторить позже
В треугольнике
и
— высоты, пересекающиеся в точке
Найдите
Ответ дайте в градусах.
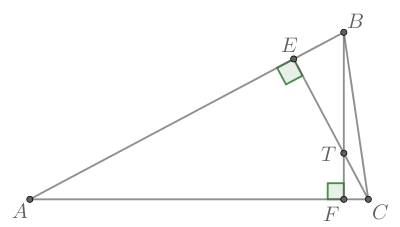
Так как и
— смежные, то
Сумма острых углов в прямоугольном треугольнике равна поэтому
Треугольник — прямоугольный, поэтому
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
и
— медианы,
— точка пересечения
и
Найдите
Ответ дайте в градусах.
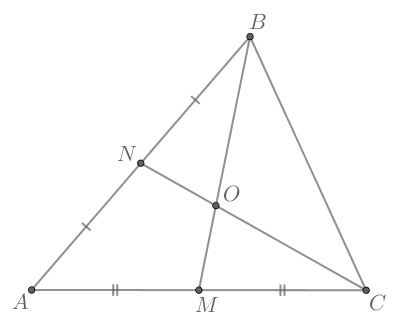
В треугольнике медианы точкой пересечения делятся в отношении считая от вершины. Так как
то
Тогда треугольник — равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда
Так как сумма углов в треугольнике равна то
Ошибка.
Попробуйте повторить позже
В треугольнике
и
— медианы,
— точка пересечения
и
Найдите
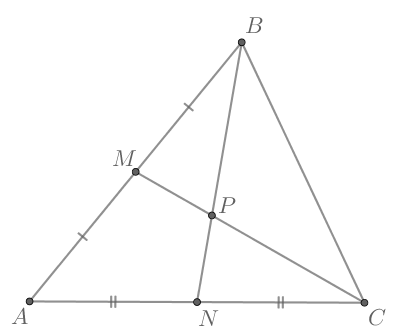
Так как сумма углов в треугольнике равна
Значит, треугольник — равнобедренный и
В треугольнике медианы точкой пересечения делятся в отношении считая от вершины. Так как
то
и
— вертикальные, а значит, равные.
Таким образом, треугольники и
равны по двум сторонам и углу между ними, тогда
Ошибка.
Попробуйте повторить позже
В треугольнике на стороне
отмечены точки
и
так, что
— середина
а
— медиана в треугольнике
Во сколько раз
длиннее, чем
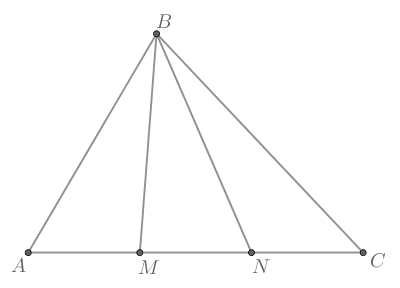
По условию имеем
Тогда
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса, причем
Найдите

По теореме о биссектрисе (биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам) имеем:
Тогда
Ошибка.
Попробуйте повторить позже
В треугольнике
— высота,
Найдите
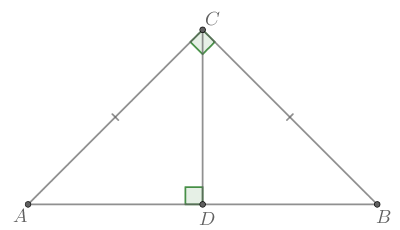
В равнобедренном треугольнике высота, проведённая к основанию, является биссектрисой и медианой, тогда
В равнобедренном треугольнике углы при основании равны, тогда
Так как — биссектриса,
то есть в треугольнике
углы при основании
равны, тогда треугольник
— равнобедренный, то есть
Ошибка.
Попробуйте повторить позже
В треугольнике
— высота,
Найдите
Ответ дайте в градусах.
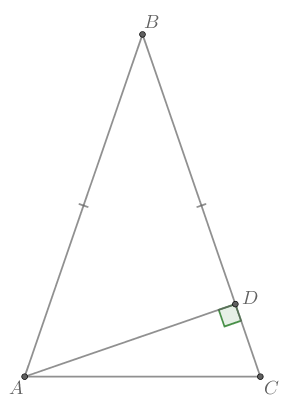
Так как — высота,
тогда
В равнобедренном треугольнике углы при основании равны, тогда
Сумма углов треугольника равна тогда
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса,
— такая точка на
что
Найдите
Ответ дайте в
градусах.

Сумма углов треугольника равна тогда имеем:
Так как — биссектриса, то
Треугольники и
равны по двум сторонам и углу между ними,
тогда
Из треугольника
имеем:
Тогда получаем
Значит, искомый угол равен
Ошибка.
Попробуйте повторить позже
В треугольнике
и
— высоты, пересекающиеся в точке
Найдите
Ответ дайте в градусах.
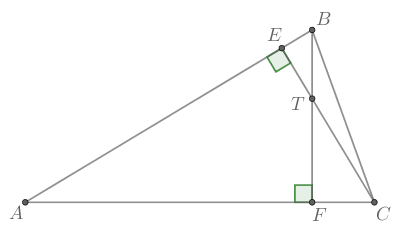
Углы и
смежны, поэтому
По сумме углов четырехугольника
Таким образом,
Ошибка.
Попробуйте повторить позже
Острый угол прямоугольного треугольника
равен
Найдите угол между высотой
и медианой
проведенными из вершины прямого угла
Ответ дайте в градусах.
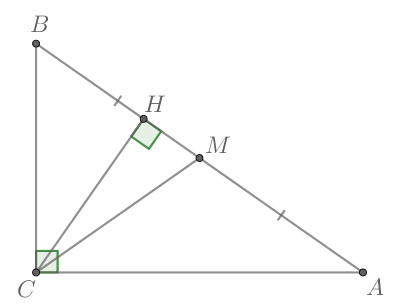
Так как медиана, опущенная из вершины прямого угла треугольника, равна половине гипотенузы, то треугольник —
равнобедренный, то есть
Следовательно,
В прямоугольном треугольнике
Тогда
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
— биссектриса,
Найдите
Ответ дайте в градусах.
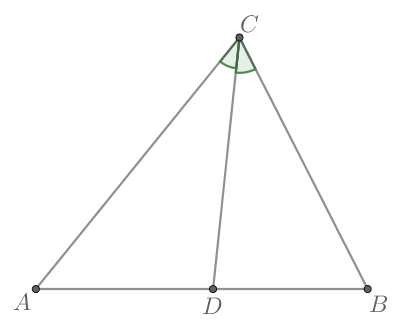
Так как — биссектриса, то
Тогда имеем:
Сумма углов треугольника равна тогда для треугольника
получаем
Окончательно для треугольника имеем:



