1.22 Внешние углы многоугольника и тригонометрия
Ошибка.
Попробуйте повторить позже
В треугольнике
Найдите косинус внешнего угла при вершине
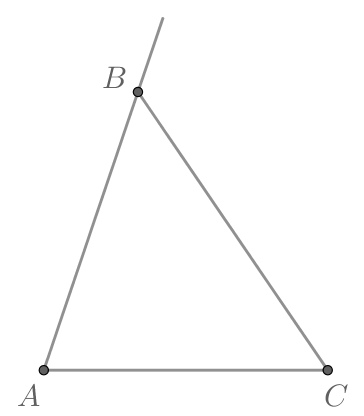
Синусы смежных углов равны: тогда синус внешнего угла при вершине
равен
Используя основное тригонометрическое тождество (), находим, что косинус внешнего угла при вершине
равен
Так как то внешний угол при вершине
— тупой, следовательно, его косинус отрицателен. Косинус внешнего
угла при вершине
равен
Ошибка.
Попробуйте повторить позже
В треугольнике
Найдите синус внешнего угла при вершине

Так как то
Внешний угол треугольника равен сумме углов треугольника, не смежных с ним, тогда
внешний угол при вершине
равен
а его синус равен
При помощи основного тригонометрического тождества находим но в равнобедренном треугольнике угол при
основании всегда острый, тогда
следовательно,
Ошибка.
Попробуйте повторить позже
Дан треугольник причем
Найдите синус угла
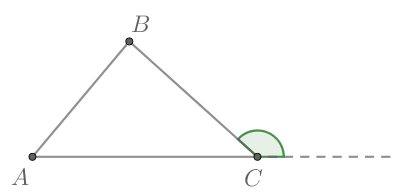
Т.к. в треугольнике внешний угол при вершине равен сумме углов
и
то и
Т.к. синусы смежных углов равны, то
Ошибка.
Попробуйте повторить позже
В треугольнике известно, что
Найдите косинус угла
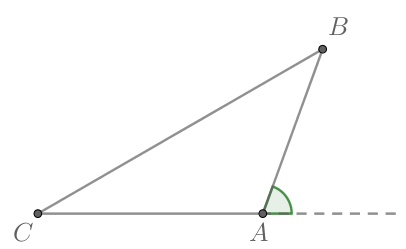
Т.к. в треугольнике внешний угол при вершине равен сумме углов
и
то
Т.к. косинусы смежных углов отличаются только знаком, то
Ошибка.
Попробуйте повторить позже
В невыпуклом четырёхугольнике (
) сторону
продолжили за точки
и
получив по одному внешнему
углу при вершинах
и
Найдите косинус внешнего угла при вершине
если косинус внешнего угла при
вершине
получился
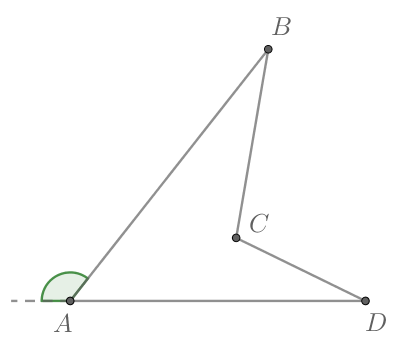
Косинусы смежных углов противоположны:
Косинус внешнего угла при вершине равен
тогда
Так как косинус внешнего угла равен минус косинусу угла, смежного с ним, то косинус внешнего угла при вершине равен
Ошибка.
Попробуйте повторить позже
К каждому углу трапеции построено по одному внешнему углу. Найдите сумму косинусов этих внешних
углов.
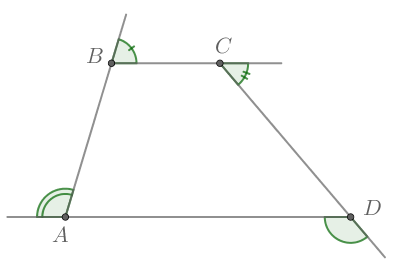
Пусть внешние углы построены как на рисунке (при каждой вершине может быть два внешних угла, но их
градусные меры совпадают, а значит, и косинусы этих углов равны и ответ не зависит от выбора угла при каждой
вершине).
Сумма внешних углов при вершинах и
равна
(так как внешний угол при вершине
и
равны, как
внутренние накрест лежащие при параллельных прямых и секущей).
Аналогично сумма внешних углов при вершинах и
равна
следовательно, сумма косинусов внешних углов при вершинах и
равна 0;
аналогично сумма косинусов внешних углов при вершинах и
равна 0. Таким образом, сумма косинусов внешних углов
равна 0.
Ошибка.
Попробуйте повторить позже
Дан выпуклый четырехугольник причем
Найдите синус внешнего угла при вершине
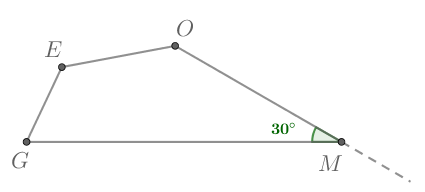
Т.к. сумма углов любого выпуклого четырехугольника равна то
Следовательно, Т.к. синусы смежных углов равны, то
Ошибка.
Попробуйте повторить позже
Дан выпуклый пятиугольник, причем сумма четырех его внутренних углов равна Найдите квадрат косинуса внешнего угла
при вершине оставшегося пятого угла.
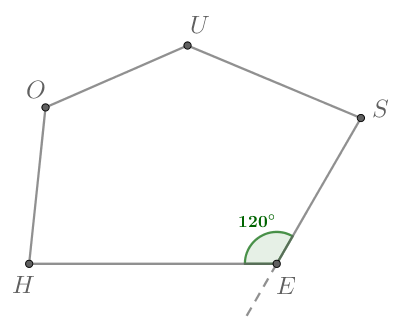
Т.к. сумма внутренних углов выпуклого -угольника вычисляется по формуле
то сумма внутренних углов нашего
пятиугольника равна
Следовательно, если
Следовательно,
Значит,
Ошибка.
Попробуйте повторить позже
В четырёхугольнике с тупыми углами
и
продолжение стороны
за точку
и продолжение стороны
за
точку
пересеклись в точке
под прямым углом. При этом
Найдите
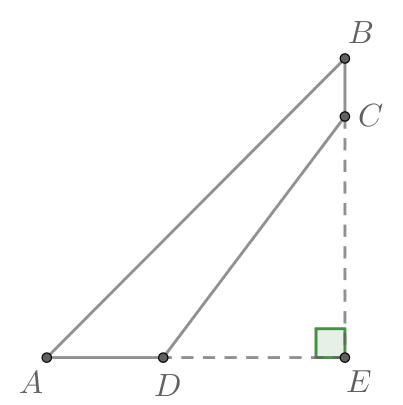
Из основного тригонометрического тождества с учётом того, что — острый, получаем:
Из определений синуса и косинуса острого угла в прямоугольном треугольнике получаем, что
Так как синусы смежных углов равны, то
Ошибка.
Попробуйте повторить позже
Дан выпуклый пятиугольник причем известно, что
Найдите синус внешнего угла при
вершине
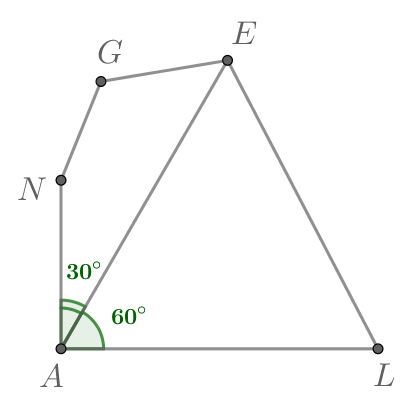
Т.к. то
равен либо
либо
Но пятиугольник выпуклый, а это значит, что все его внутренние
углы меньше
следовательно,
и весь
(иначе весь
был бы равен
).
Значит, и внешний угол при вершине равен
а его синус таким образом равен
Ошибка.
Попробуйте повторить позже
В треугольнике косинус угла между стороной
и высотой к стороне
равен
Найдите синус внешнего угла
треугольника при вершине
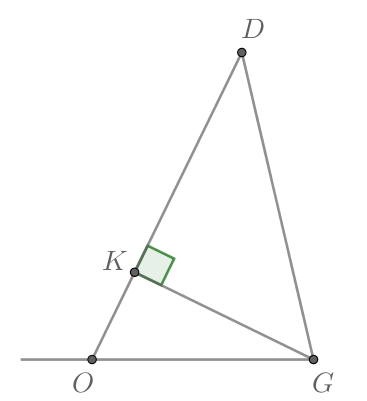
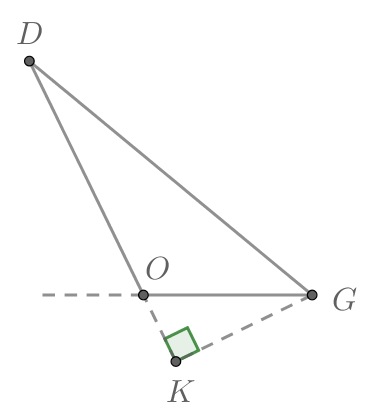
Т.к. синусы смежных углов равны, то Рассмотрим два случая: когда
— острый и когда тупой. Пусть
— та самая высота из условия.
В первом случае из прямоугольного треугольника
Во втором случае из прямоугольного треугольника


