.02 Равноускоренное движение

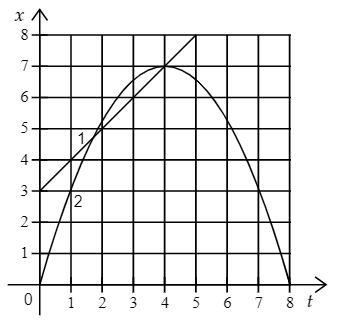
1 способ:

Скорость — это производная по времени от координаты . Геометрический смысл производной — тангенс угла наклона касательной, следовательно, чтобы проекции скоростей этих тел были приблизительно одинаковыми, ко второму графику надо провести касательную, параллельную первой прямой. Эта касательная примерно пройдет через точку с.

2 способ:
Напишем уравнения движения данных тел. Изменение координаты первого тела линейное, следовательно первое тело движется равномерно:

Так как зависимость координаты второго тела квадратичная, графиком её является парабола, то второе тело движется равноускоренно:

Так как первое тело движется равномерно, его скорость остается неизменной. Выразим скорость из уравнения (1):

По условию задачи:

Запишем уравнение (2) другим способом. Зависимость координат второго тела — парабола с вершиной при и с корнями (т.е. точками пересечений с осью ) и . Тогда получим:

Выразим из уравнения (3) и подставим координаты вершины параболы:

Тогда уравнение (3) преобразуется в:

Заметим, что скорость — производная пути. Найдем производную пути из уравнения (4). Получим:

Выразим отсюда время , которое и необходимо нам найти по условию задачи: