Электростатика —Каталог задач по ЕГЭ - Физика

Ошибка.
Попробуйте повторить позже

Задача 1#26348

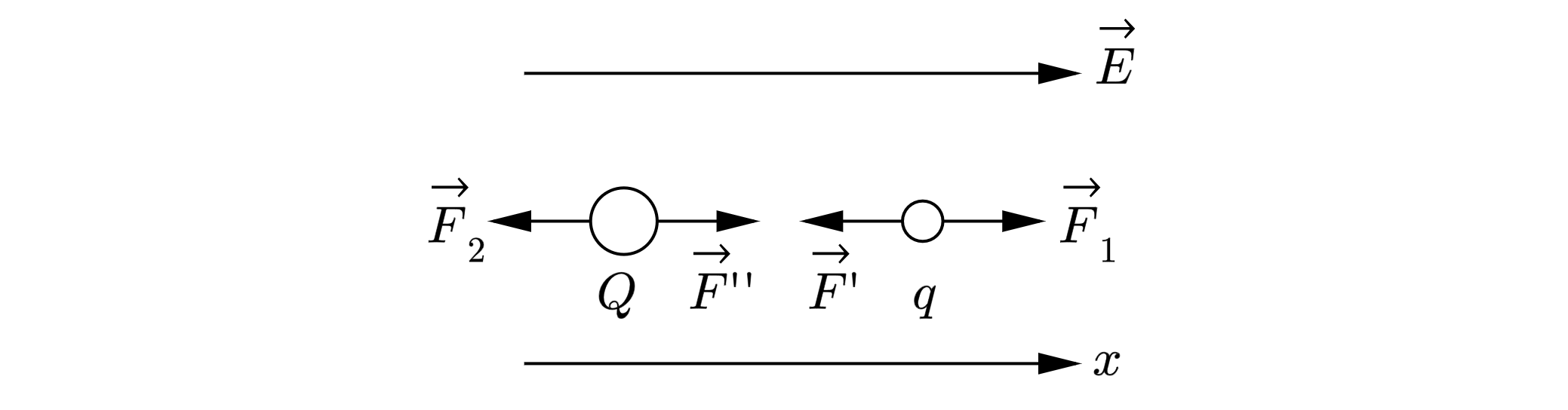
Три маленьких одинаково заряженных шарика массой $m = 4,0$ г каждый подвешены на шелковых нитях длиной $l = 1,0$ м. Верхние концы нитей закреплены в одной точке. Расстояние от каждого шарика до двух других одинаково: $a= 5,0$ см. Каков заряд $q$ каждого шарика?

Показать ответ и решение

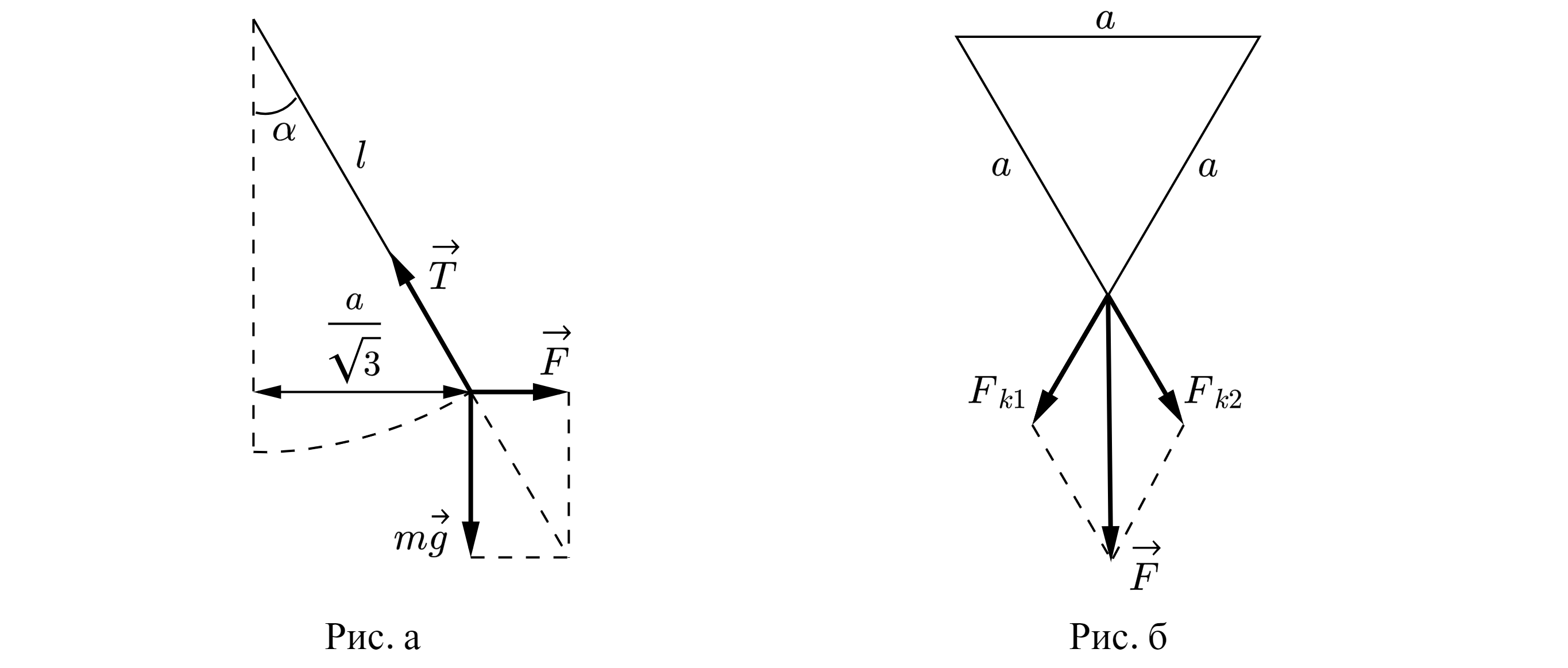
Каждый из шариков отклонен от центра треугольника на расстояние $a √3-$ . Отсюда следует (см. рис. а)

F tgα = mg-,

что на шарик действует горизонтальная отклоняющая сила

F = mgtgα≈ mg √a-, (1) l 3

здесь учтено, что $a << l$ и $α << 1$ , $tgα ≈ α.$ При этом сила $F$ является равнодействующей силой сил Кулона $Fk1$ и $Fk2$ (см. рис. б). Они одинаковы по модули и равны:

2 Fk1 = Fk2 = kq2. a

Тогда по теореме косинусов:

( 2)2 ( 2)2 ( 2)2 2 - F2 = F2k1+ F2k2− 2Fk1Fk2cos120∘ = 2 kq2 + kq2- ⋅= 3 kq2- ⇒ F = kq2√ 3. (2) a a a a

Приравняв (1) и (2) получим:

q2√ - a ∘-amg ∘ 0,05⋅4⋅10−3⋅10 ka2 3= mg √--⇒ q = a 3lk-= 0,05 --3-⋅1⋅9⋅109--≈ 13,6 нК л l 3

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: описано состояние равновесия каждого из шариков, записан закон Кулона);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 2#11067

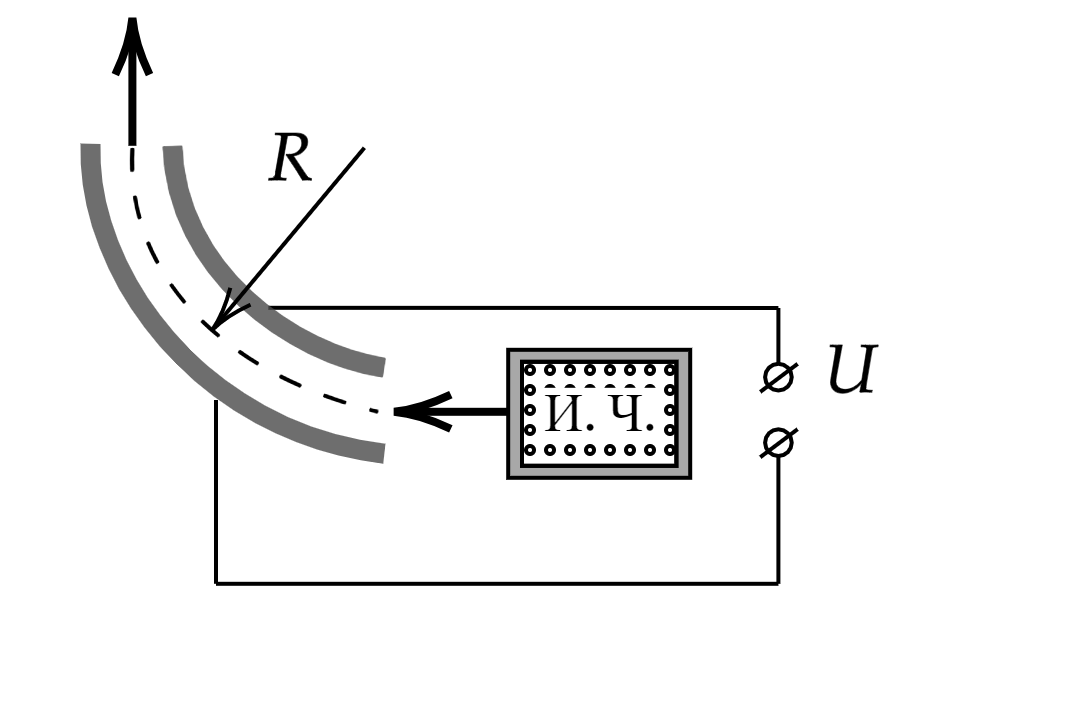
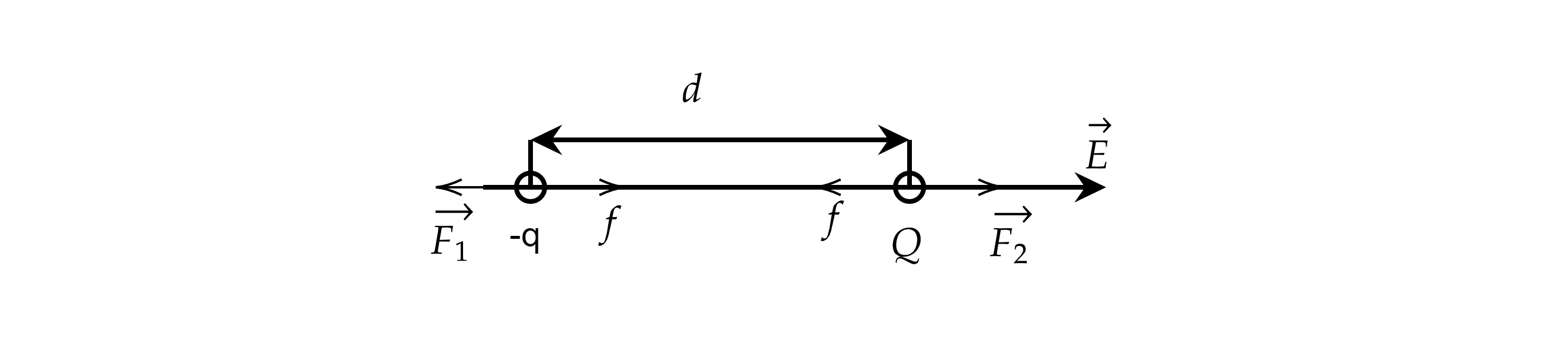
На рисунке показана схема устройства для предварительного отбора заряженных частиц из источника частиц (и.ч.) для последующего детального исследования. Устройство представляет собой конденсатор, пластины которого изогнуты дугой радиусом R. Предположим, что в промежутке между обкладками конденсатора, не касаясь их, пролетают молекулы интересующего нас вещества, потерявшие один электрон. Во сколько раз нужно изменить напряжение на обкладках конденсатора, чтобы сквозь него могли пролетать такие же ионы, но имеющие в 2 раза большую кинетическую энергию? Считать, что расстояние между обкладками конденсатора мало, напряжённость электрического поля в конденсаторе всюду одинакова по модулю, а вне конденсатора электрическое поле отсутствует. Влиянием силы тяжести пренебречь.

Источники: Демидова 2019 | Демидова 2020

Показать ответ и решение

Ион пролетит сквозь конденсатор, не коснувшись его пластин, только в том случае, если будет двигаться по окружности радиуса $R$ . Так как силой тяжести иона пренебрегаем, то на ион с силой F действует только электрическое поле конденсатора с напряженностью $E$ . Так как конденсатор искривлен, то направление напряженности будет непрерывно меняться.

$PIC$

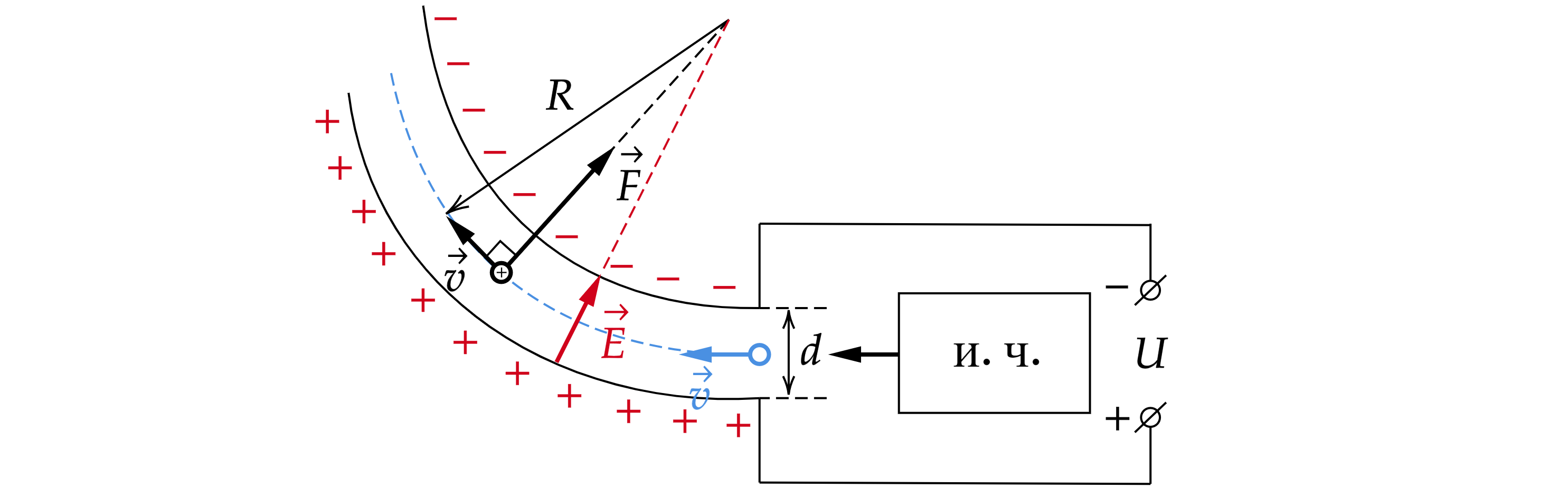
На частицу будет действовать электрическая сила, равная

F =qE,

Напряженность поля равна

E = U, d

Тогда

U- F = qd ,

где $q$ – заряд, $U$ – напряжение между обкладками конденсатора, $d$ – расстояние между обкладками конденсатора.
Эта сила по второму закону Ньютона будет порождать центростремительное ускорение, равное

v2 a = R-

При этом второй закон Ньютона будет выглядеть следующим образом

⃗F =m ⃗a

В проекции на ось, направленную в центр траектории

2 F = ma ⇒ qU-= m v- d R

Кинетическая энергия выражается формулой:

W = mv2- 2

Выразим из второго закона Ньютона формулу кинетической энергии

mv2 qUR -2--= -2d-= W

Откуда напряжение равно

U = 2W-d qR

из соотношения видно, что напряжение надо увеличить в 2 раза.

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: записана формула силы электрической, записана формула связи напряженности с напряжением, сказано, что частица будет обладать центростремительным ускорением, записан второй закон Ньютона в проекции на радиальное направление, записана формула кинетической энергии. Выражена формула, описывающая зависимость между кинетической энергией и напряжением);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 3#11070

В стол воткнута нижним заостренным концом спица, наклоненная под углом $∘ α= 30$ к горизонту. У ее нижнего конца закреплена маленькая заряженная бусинка. На спицу надета другая такая же заряженная бусинка, которая может скользить по спице без трения. Заряды бусинок одинаковы и равны $q = 1$ мкКл, масса бусинки $m = 20$ г. Определите расстояние $l$ между бусинками, если они находятся в равновесии. Сделайте рисунок с указанием сил, действующих на верхнюю бусинку.

Источники: Основная волна 2020

Показать ответ и решение

Расставим силы, действующие на верхнюю бусинку

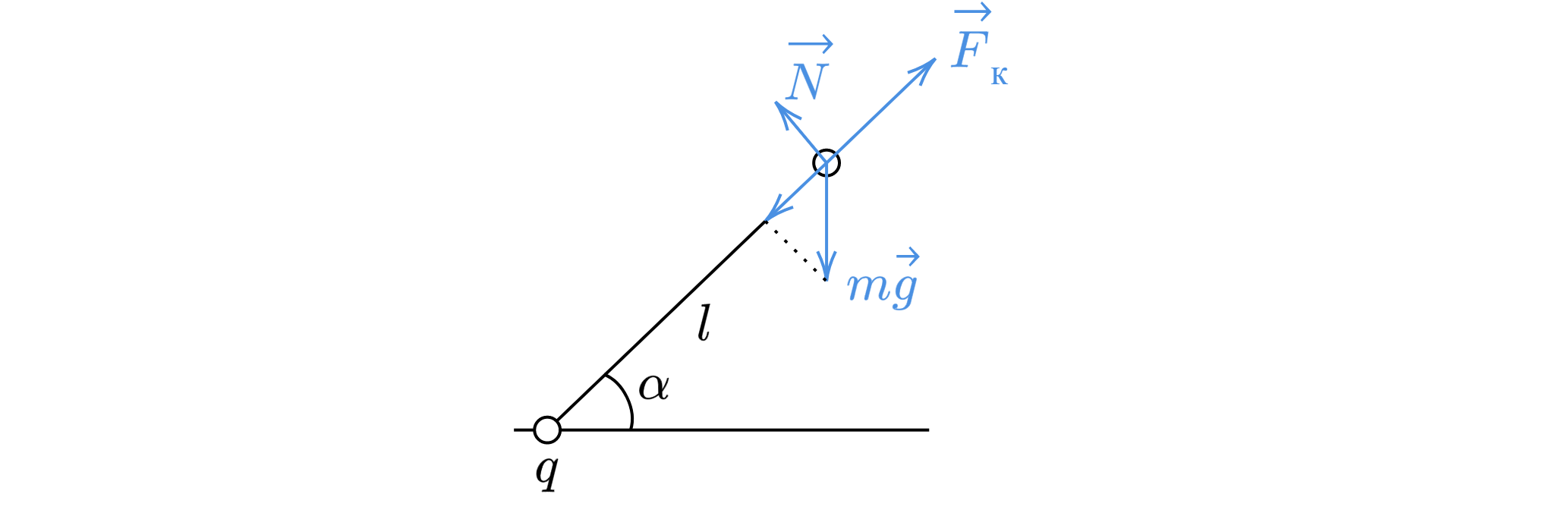
Так как бусинки находятся в равновесии, то из второго закона Ньютона

⃗N + m⃗g+ F⃗k = 0,

где $N$ – сила реакции опоры стержня, $Fk$ – сила Кулона.
Сила взаимодействия между зарядами равна

2 Fk = kq2 . (1) l

Тогда в проекции второго закона Ньютона на ось, совпадающую с осью спицы и перпендикулярную ей:

({N = mg cosα (mg sin α= Fk

С учетом (1)

∘ ------- ∘ ------------------ mg sinα = kq2⇒ l = q ---k---= 1⋅10−6 К л ------9⋅109-------= 0,3 м l2 mg sinα 0,02 кг⋅10 Н/кг ⋅0,5

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: второй закон Ньютона. Записан закон Кулона. Сказано, что в полложении равновесия бусинки покоятся и их ускорение равно нулю);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 4#11071

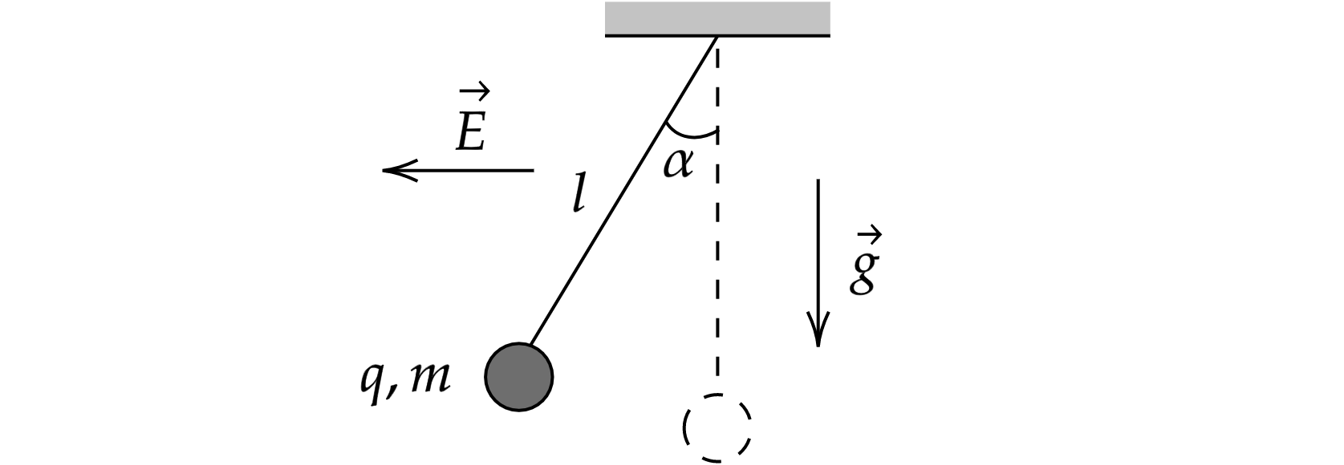
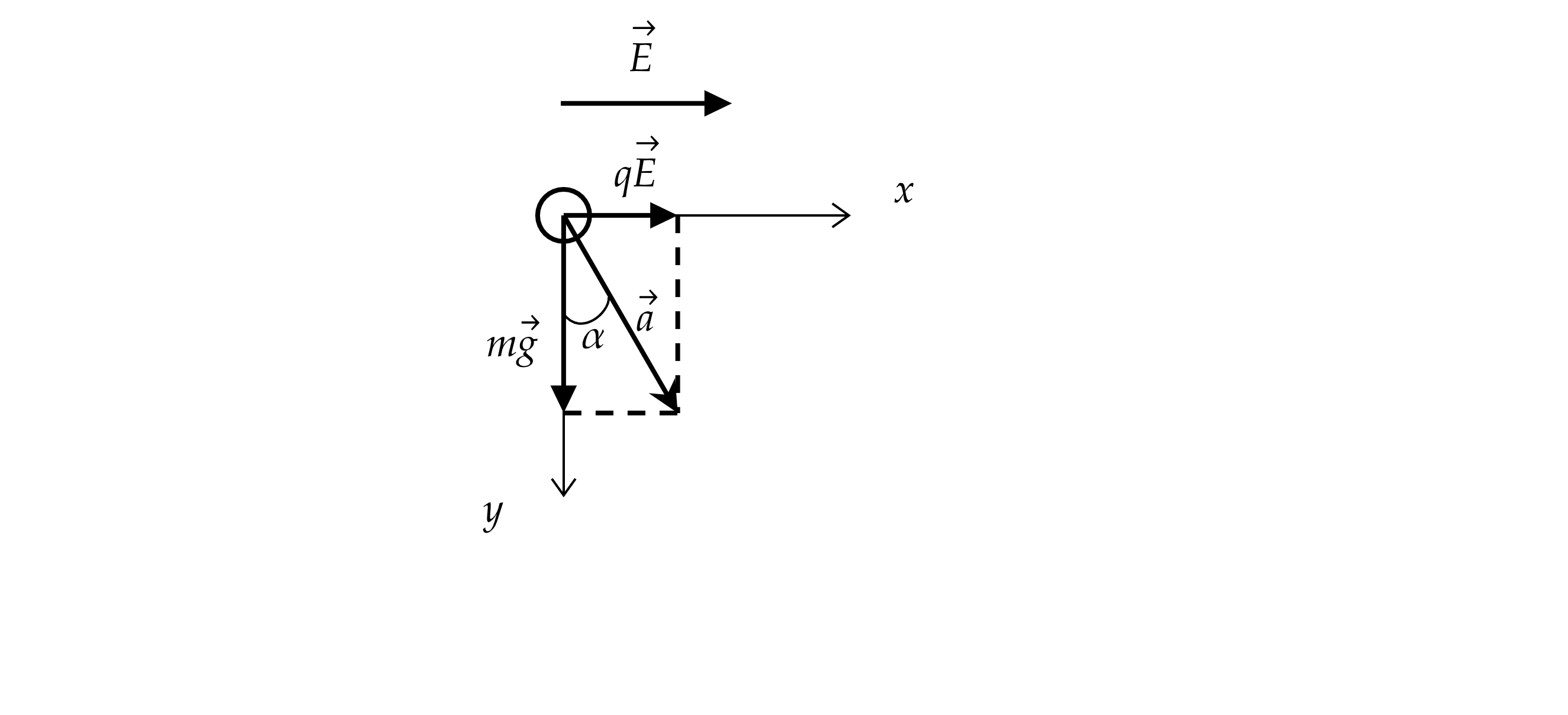
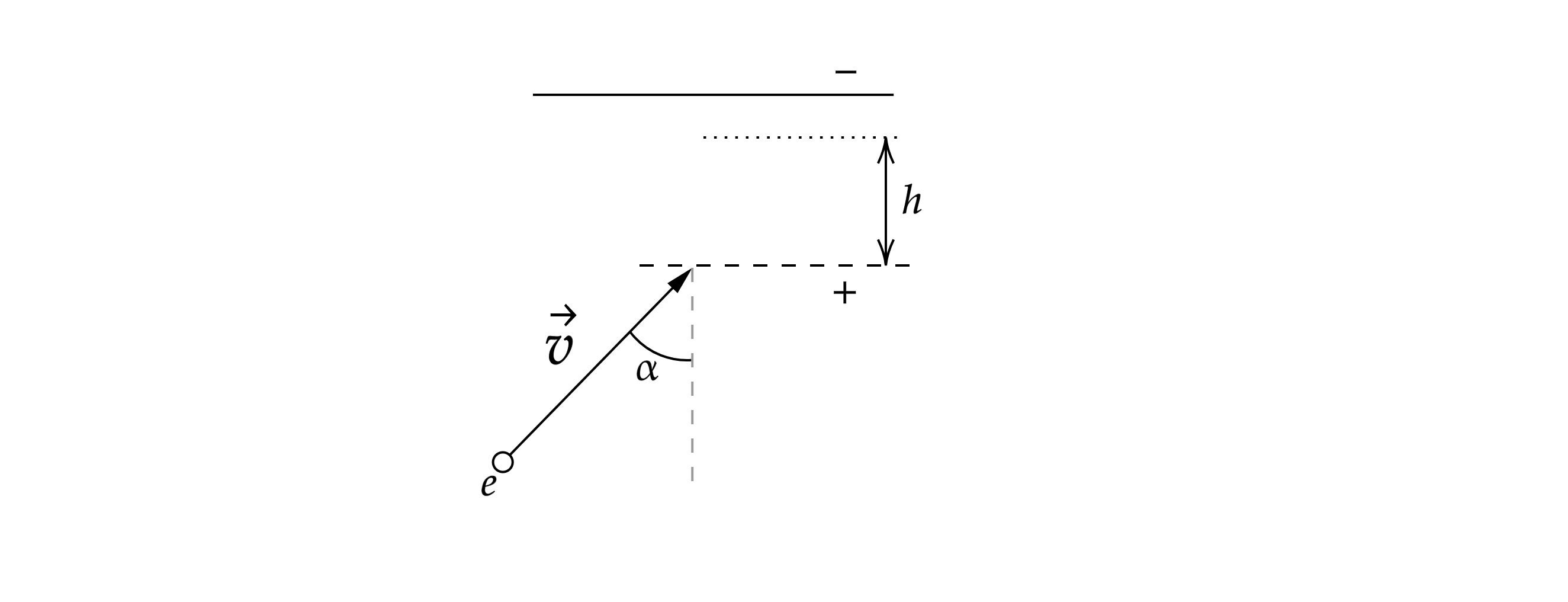
Маленький шарик массой m с зарядом $q =5$ нКл, подвешенный к потолку на лёгкой шёлковой нитке длиной $l = 0,8$ м, находится в горизонтальном однородном электростатическом поле $E⃗$ с модулем напряжённости поля $E =6 ⋅106$ В/м (см. рисунок). Шарик отпускают с нулевой начальной скоростью из положения, в котором нить вертикальна. В момент, когда нить образует с вертикалью угол $α = 30∘$ , модуль скорости шарика $v$ = 0,9 м/с. Чему равна масса шарика $m$ ? Сопротивлением воздуха пренебречь.

Источники: Демоверсия 2020 | Демидова 2020

Показать ответ и решение

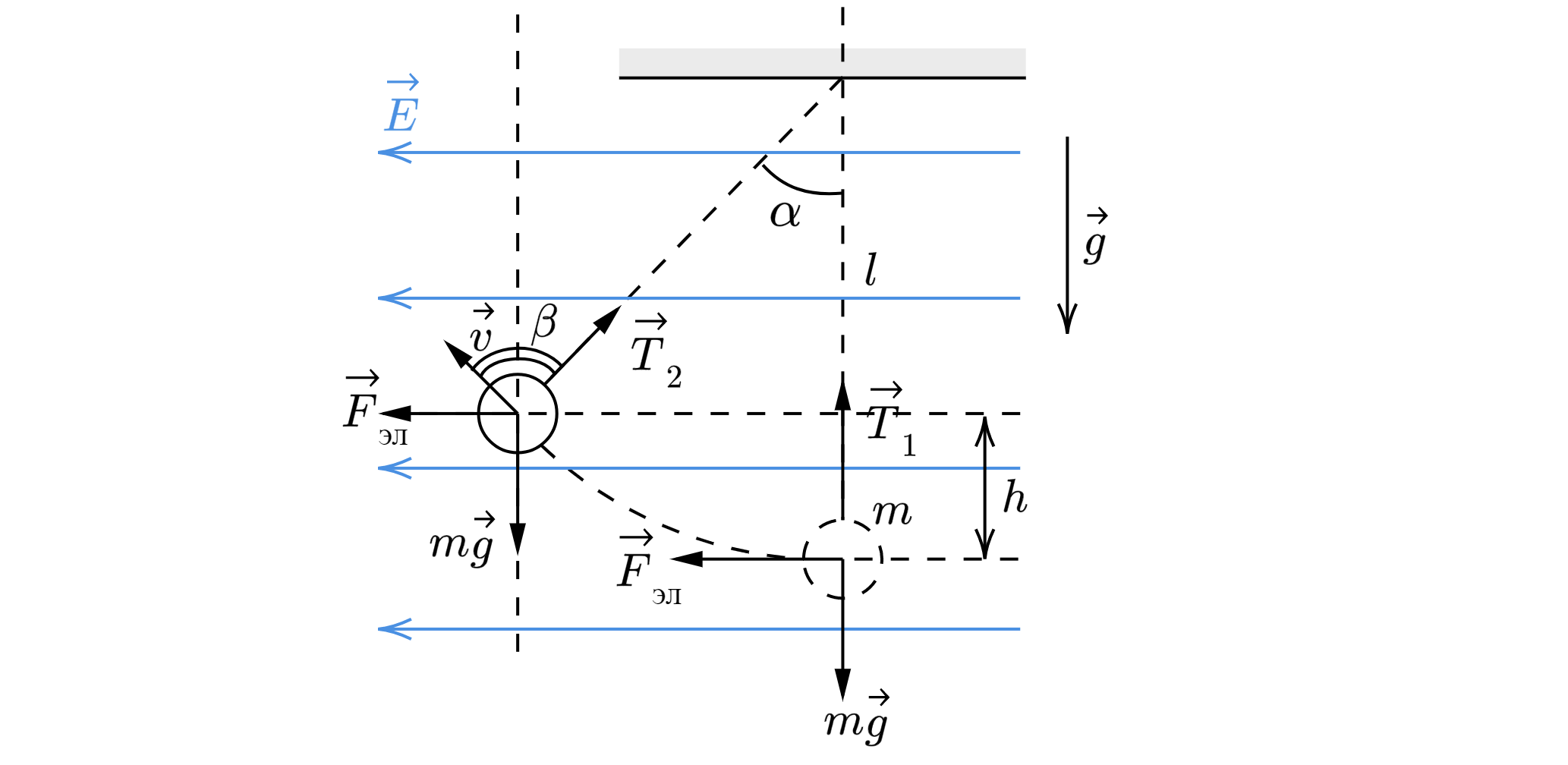
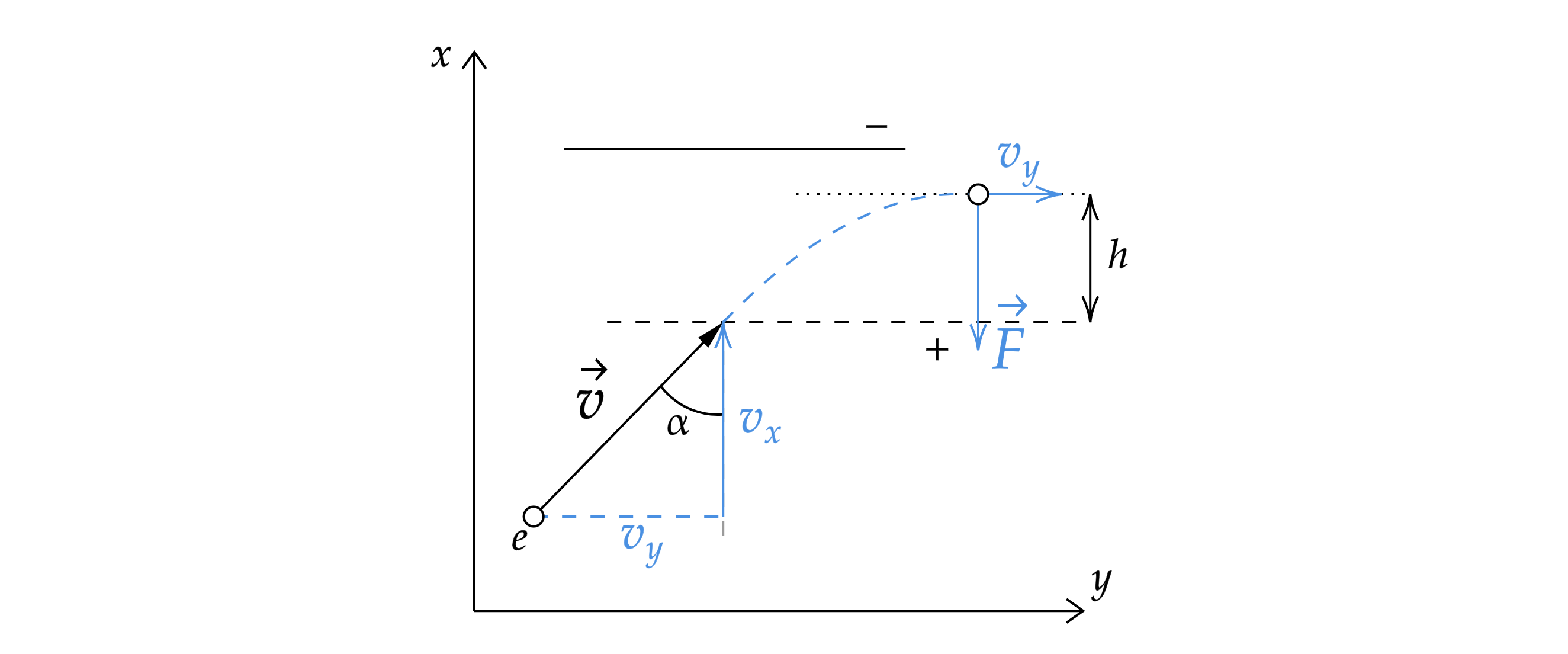
При перемещении шарика из начального положения в конечное на него будут действовать 3 силы: сила тяжести $mg$ , электрическая сила $qE$ и сила натяжения нити $T$ .
Сила тяжести направлена вниз, при этом она направлена противоположно перемещению шарика по вертикали, значит её работа равна:

Amg = −mgh,

где $h$ – смещение шарика по вертикали.
Электрическая сила направлена влево и сонаправлена перемещению по горизонтали

AqE = qES.

Здесь $S$ – смещение шарика по горизонтали.
Сила натяжения нити направлена вдоль нити. Рассмотрим некоторое положение шарика. Пусть в этот момент сила натяжения равна $T0$ , а скорость шарика $v0$ , при этом скорость всегда направлена по касательной к траектории. В этот момент мощность силы натяжения нити равна:

N0 = T0⋅v0 cosβ,

где $β$ – угол между силой натяжения и скоростью.
Так как $α = 90∘$ , то $cosα =0$ , следовательно, $N0$ тоже равно нулю. Так как мы рассмотрели случайное положение, значит, это справедливо для любого положения шарика, следовательно, при движении шарика мощность, а, следовательно, работа силы натяжения равна нулю.

AT = 0.

По закону сохранения энергии работы сил будут формировать кинетическую энергию

Ek = Amg + AqE + AT = −mgh + qES (1)

Из геометрической картины имеем, что $h= l(1− cosα) (2)$ , а $S = lsinα (3)$ . Распишем изменение кинетической энергии в уравнении (1) и подставим в него (2) и (3)

mv2 --2-= − mgl(1 − cosα)+ qElsinα

Отсюда масса шарика

−9 6 m = ----2qEl-sinα----= -2-⋅5-⋅10---Кл-⋅6-⋅10--В/м⋅0,8 м-⋅0√,5 ≈ 8,1⋅10− 3 кг v2+ 2gl(1− cosα) 0,81 м2/с2+ 2⋅10 Н/ кг⋅0,8 м(1−-3-) 2

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон изменения механической энергии материальной точки, формулы для работы силы тяжести и работы однородного электрического поля при перемещении заряженного тела);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 5#11073

Пылинка, имеющая массу $−11 10$ кг и заряд $− 14 q =− 1,8 ⋅10$ Кл влетает в электрическое поле вертикального плоского конденсатора в точке, находящейся посередине между его пластинами (см. рисунок, вид сверху). Чему должна быть равна минимальная скорость, с которой пылинка влетает в конденсатор, чтобы она смогла пролететь его насквозь? Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение на пластинах конденсатора 5 000 В. Система находится в вакууме.

Показать ответ и решение

Так как частица заряжена отрицательно, то электрическая сила, действующая на частицу будет направлена противоположно вектору напряженности. Так как по условию на рисунке показан вид сверху, то можно утверждать, что сила тяжести направлена в плоскость чертежа и ее проекция на выбранные нами оси равна нулю.

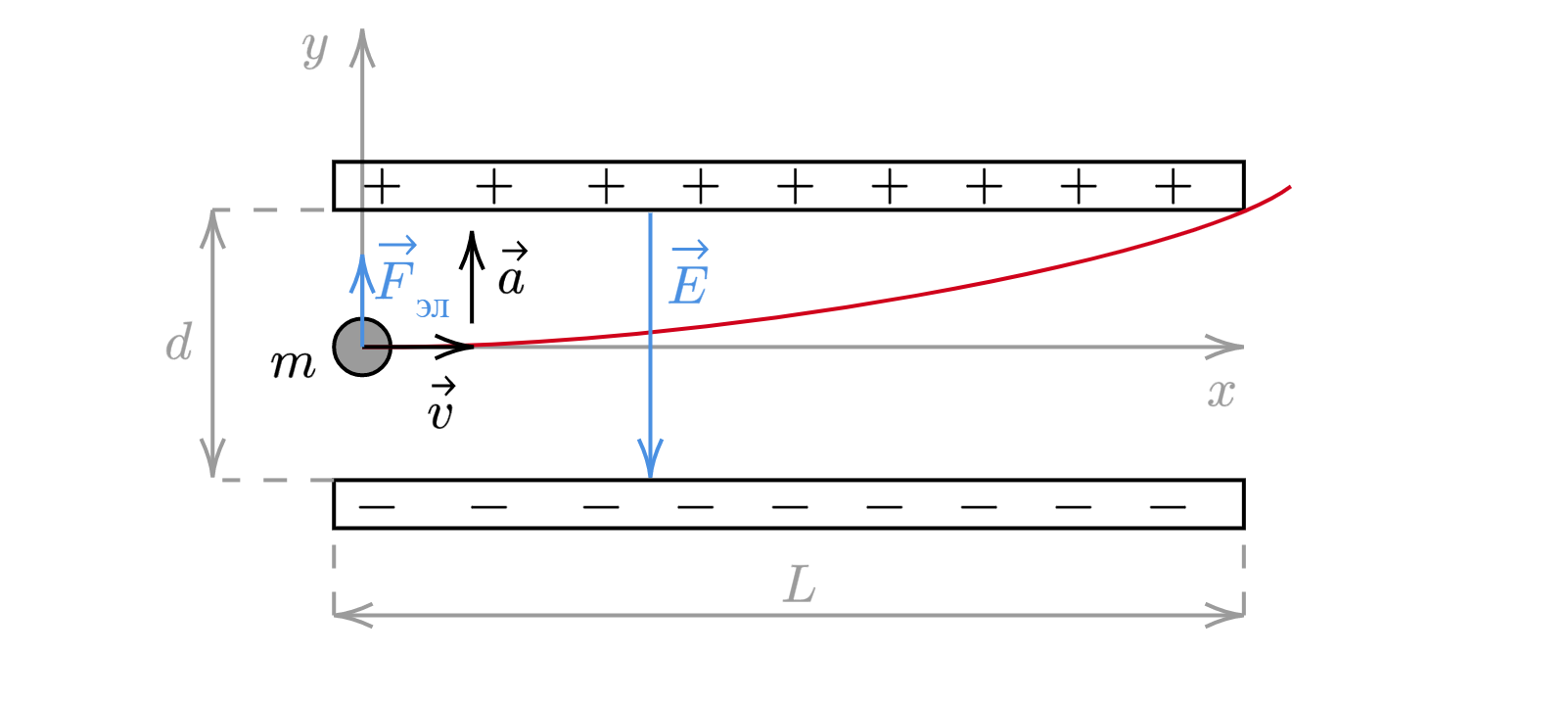
Запишем второй закон Ньютона:

⃗Fэл +m ⃗g = m ⃗a,

где $Fэл$ – электрическая сила, $g$ – ускорение свободного падения, $a$ – ускорение тела.
Спроецируем на оси $x$ и $y$

( { x 0= max ( y Fэл = may

Вдоль оси $x$ – движение равномерное, вдоль оси $y$ – равноускоренное. Электрическая сила взаимодействия равна

Fэл =|q|E,

где $q$ – заряд тела, $E$ – вектор напряженности.
Напряженность между пластинами конденсатора равна

E = U, d

где $U$ – напряжение между пластинами, $d$ – расстояние между пластинами. Тогда ускорение по $y$ равно:

ay = Fэл = |q|E-= |q|U. m m dm

Координата по $y$ описывается уравнением

d ayt2- y = 2 + v0yt+ 2 .

Здесь $v0y = 0$ – скорость при влете пылинки в конденсатор.
Минимальная скорость будет тогда, когда пылинка при вылете из конденсатора будте находиться на окраине пластины:

2 2 y = ayt-⇒ d= |q|Ut- 2 2 2md

Откуда

∘---- t= d2m-- |q|U

Так как движени по оси $x$ :

L = vt

∘ ---- ∘------−14----- vmin = L-=L ⋅ |q|2U-= 0,1 ⋅ 1,8⋅102--⋅−510100= 30 м/с t d m 0,01 ⋅10

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: второй закон Ньютона, введена сила тяжести, указано, что ее направление перпендикулярно плоскости чертежа, формула для силы, действующей на электрический заряд, находящийся в электрическом поле F = qE, записана формула, связывающая напряженность однородного электрического поля с разностью потенциалов на обкладках конденсатора, указан разный характер движения частицы - равномерный вдоль оси ОХ и равноускоренный для оси ОУ, записаны уравнения кинематики движения частицы по всем необходимым для решения задачи координатным осям);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 6#11075

Полый шарик массой $m = 0,4$ г с зарядом $q = 8$ нКл движется в горизонтальном однородном электрическом поле, напряжённость которого $E = 500$ кВ/м. Какой угол $α$ образует с вертикалью траектория шарика, если его начальная скорость равна нулю?

Показать ответ и решение

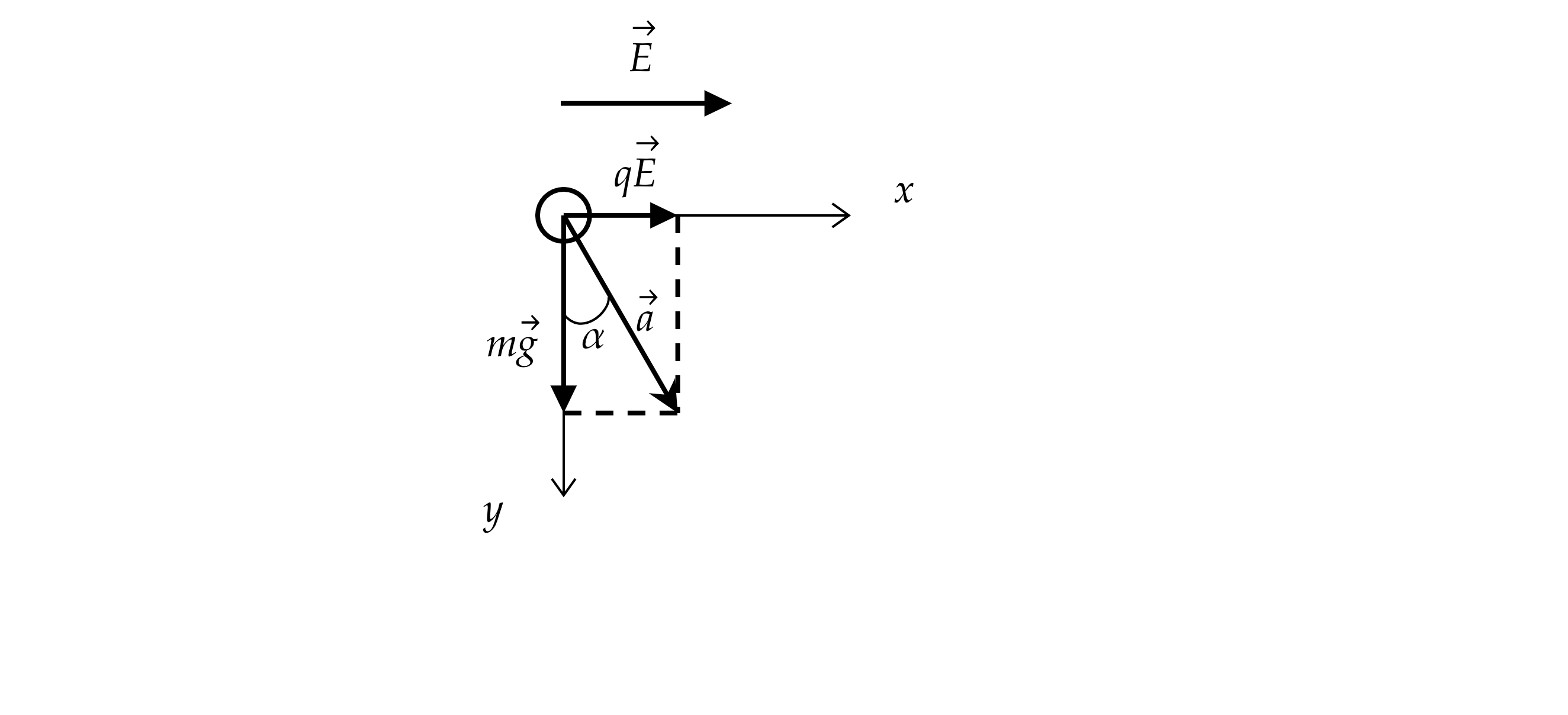
Запишем второй закон Ньютона для пылинки

q⃗E +m ⃗g = m ⃗a

На ось Ох:

qE =max

На ось Оу:

mg = may

Тогда тангес угла равен

ax qE 8⋅10−9 Кл⋅500⋅103 В/м tgα= ay = mg-= ---4⋅10−4 кг⋅10 м/с2-

Так как $tgα= 1$ , то угол равен $45∘$

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: второй закон Ньютона, формула силы электрической);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 7#11076

Полый шарик массой $m = 0,4$ г с зарядом $q = 8$ нКл движется в горизонтальном однородном электрическом поле, угол траектории равен $45∘$ . Найдите чему равна напряженность электрического поля( $E$ ).

Показать ответ и решение

Запишем второй закон Ньютона для пылинки

q⃗E +m ⃗g = m ⃗a

На ось Ох:

qE =max

На ось Оу:

mg = may

Тогда тангес угла равен

ax qE tgα = ay = mg

Выразим напряженность:

tgαmg E = --q---

Так как угол равен 45 $∘$ , то $tgα = 1$ . Найдем напряженность

E = 4⋅10−4 кг-⋅10-м/с2⋅1= 500 кВ/ м 8 ⋅10−9 Кл

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: записан второй закон Ньютона, формула силы электрической);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 8#11077

Отрицательно заряженная пластина, создающая вертикально направленное однородное электрическое поле напряженностью $E = 104$ В/м, укреплена на горизонтальной плоскости. На нее с высоты $h= 10$ см падает шарик массой $m = 20$ г, имеющий положительный заряд $q =10−5$ Кл. Какой импульс шарик передаст пластине при абсолютно упругом ударе?

Показать ответ и решение

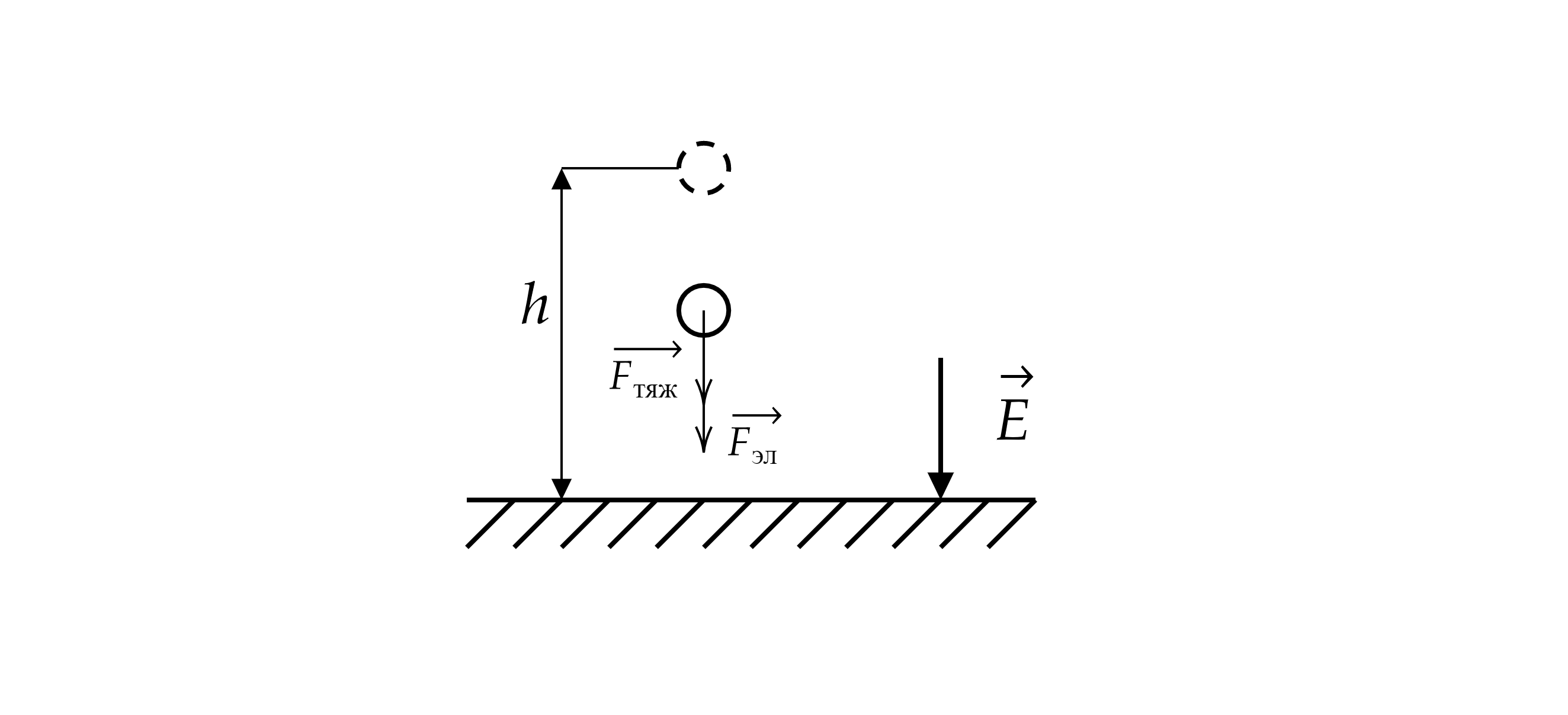
Запишем второй закон Ньютона для шарика:

mg + qE F ⃗тяж.+ F⃗эл. = ma mg + qE = ma ⇒ a= ---m---

По уравнениям кинематики координата по вертикали равна

2 ⃗y = ⃗h+ ⃗v0t+ ⃗at, 2

где $v 0$ – начальная скорость тела, $t$ – время движения.
Так как $v0 =0$ , то в момент $y = 0$

at2 ∘ 2h- 0= h − 2--⇒ t= -a .

Также скорость у пластины можно найти по формуле:

⃗v = ⃗v0 +⃗at.

С учетом $v0 = 0$ .

√ --- v = at= 2ah.

Тело в результате столкновения сохранит импульс по модулю, но изменит по направлению.

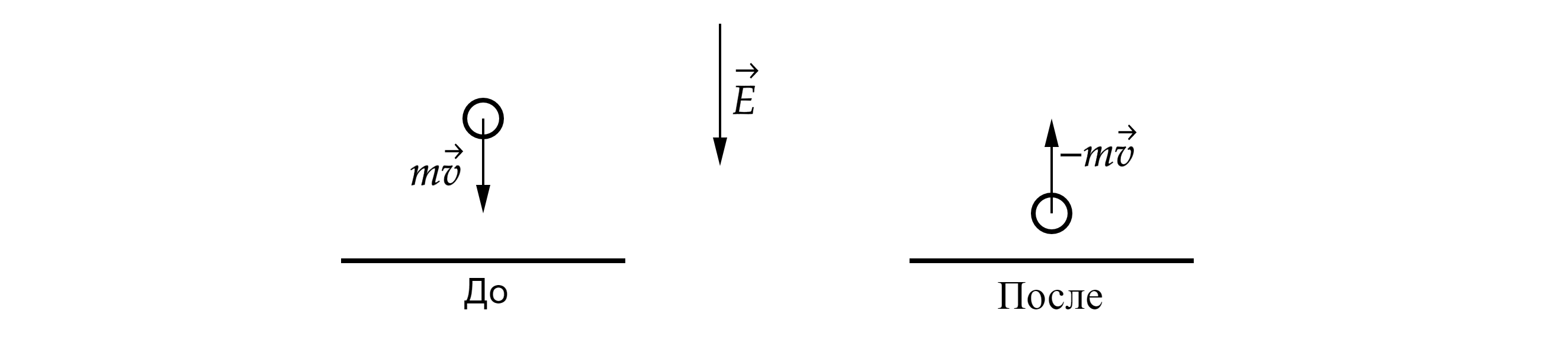
Импульс, который тело передаст в результате столкновения, равен

Δ⃗p = ⃗pk − ⃗pн,

где $pk$ – импульс тела после столкновения, $pн$ – импульс тела до столкновения

∘ ---------- ∘ ------------ |Δp|= |(− mv)− mv |=|2mv|= 2m 2hmg-+-qE = 8mh (mg +qE ) m

|Δp|= ∘8-⋅2⋅10−2 кг⋅0,1 м-(2-⋅10−2-кг⋅10м/-с+10−5-Кл⋅104 В/-м)≈ 0,07 кг ⋅м/с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: записан второй закон Ньютона, уравнения книематики для описания движения тела, записано изенение импульса тела при ударе о пластинку);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 9#20143

Шарик массой 5 г с зарядом 2 мКл подвешен на нити длиной 1 м в горизонтальном электрическом поле с напряженностью 20 В/м. Шарик сначала удерживают в нижнем положении, а затем отпускают. Найдите натяжение нити (в мН) в тот момент, когда шарик поднимется на 20 см выше начального положения. $g =10 м/с2.$

Показать ответ и решение

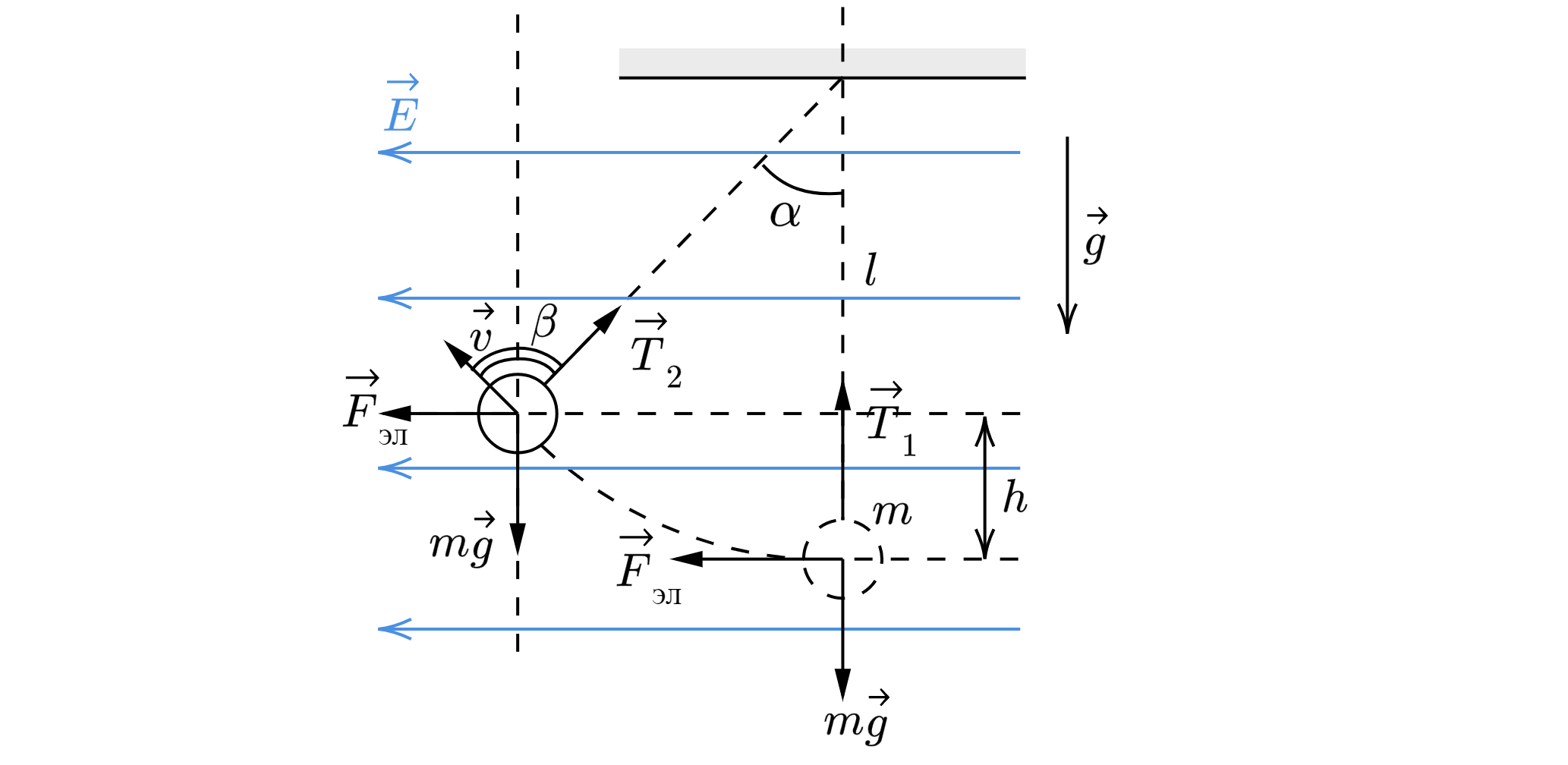
При перемещении шарика из начального положения в конечное на него будут действовать 3 силы: сила тяжести $mg$ , электрическая сила $qE$ и сила натяжения нити $T$ .
Сила тяжести направлена вниз, при этом она направлена противоположно перемещению шарика по вертикали, значит её работа равна:

Amg = −mgh,

где $h$ – смещение шарика по вертикали.
Электрическая сила направлена влево и сонаправлена перемещению по горизонтали

AqE = qES.

Здесь $S$ – смещение шарика по горизонтали.
Сила натяжения нити направлена вдоль нити. Рассмотрим некоторое положение шарика. Пусть в этот момент сила натяжения равна $T0$ , а скорость шарика $v0$ , при этом скорость всегда направлена по касательной к траектории. В этот момент мощность силы натяжения нити равна:

N0 =T0 ⋅v0 cosα,

где $α$ – угол между силой натяжения и скоростью.
Так как $α = 90∘$ , то $cosα =0$ , следовательно, $N0$ тоже равно нулю. Так как мы рассмотрели случайное положение, значит, это справедливо для любого положения шарика, следовательно, при движении шарика мощность, а, следовательно, работа силы натяжения равна нулю.

AT = 0.

По закону сохранения энергии работы сил будут формировать кинетическую энергию

Ek = Amg + AqE + AT = −mgh + qES (1)

Тогда

mv2 -2--= −mgh +qES.

Запишем также второй закон Ньютона в момент подъёма на высоту $h$ :

⃗T2+ m⃗g+ F⃗эл = m ⃗a,

где $a= v2∕l$ – центростремительное ускорение.
Спроецируем второй закон Ньютона на ось, сонаправленную с нитью:

v2 T2− mg cosα− qEsinα= m -l .

Из геометрической картины имеем, что

S = ∘l2-−-(l−-h)2; sinα = S-; cosα= l−-h. l l

Тогда

l−-h S- 2qES-−-2mgh- mg(l−-3h) 3S- T2− mg l − qE l = l ⇒ T2 = l + qE l = 92 мН.

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: формула для расчета работы силы тяжести, силы натяжения нити и силы, действующей на шарик со стороны электростатического поля, формула кинетической энергии, закон изменения кинетической энергии. Второй закон Ньютона для требуемого момента времени);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 10#20570

Две заряженные частицы помещены в однородное электрическое поле напряженностью $E$ . Частица массой $m$ несет отрицательный заряд $− q$ , а частица массой $M$ – положительный заряд $Q$ . На каком расстоянии $d$ друг от друга нужно расположить частицы, чтобы при их движении из состояния покоя расстояние между частицами оставалось неизменным?

Показать ответ и решение

Частицы расположены на одной силовой линии электрического поля (см. рисунок). При этом сила $F1$ , действующая на заряд со стороны поля $− q$ действует влево, сила $F2$ , действующая на заряд $Q$ со стороны поля действует вправо, при этом заряды притягиваются с силой $f$ .

Силы $F1$ и $F2$ равны:

F1 = qE, F2 = QE.

А сила взаимодействия зарядов:

kqQ f = d2-.

Так как расстояние между частицами по условию должно оставаться неизменным, то они движутся с одинаковым ускорением $a.$ Запишем второй закон Ньютона для каждой из частиц:

⃗F1+ ⃗f1 = m ⃗a F⃗2 +f⃗2 =M ⃗a,

при этом по третьему закону Ньютона $f1 = f2 = f$ . Спроецируем на горизонтальную ось:

−qE + kqQ-= ma QE − kqQ-= Ma. d2 d2

Домножим первое уравнение на $M$ , а второе на $m$

kqQ- kqQ-- −MqE + M d2 = Mma mQE − m d2 = mMa.

вычтем из первого второе:

∘ ------------ − MqE + M kqQ2-− mQE + m kq2Q-= 0⇒ kqQ2-(m+ M )= E (mQ +Mq )⇒ d= kqQ(M-+-m)- d d d E(mQ + Mq )

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: записана формула силы электрической, закон Кулона, второй закон Ньютона для частиц);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 11#20571

На тонкий гладкий горизонтальный диэлектрический стержень надеты две маленькие бусинки с зарядами $+ q = 60$ мкКл и $− q = −60$ мкКл, скрепленные между собой диэлектрической пружиной. Вся система находится в однородном электростатическом поле напряженностью $E =246$ кВ/м, силовые линии которого параллельны стержню. При этом пружина не деформирована. Если изменить направление поля на противоположное, оставив неизменной величину его напряженности $E$ , то длина пружины при равновесии уменьшится в 2 раза. Пренебрегая поляризацией диэлектриков, найти коэффициент жесткости пружины.

Показать ответ и решение

Частицы расположены на одной силовой линии электрического поля (см. рисунок). При этом сила $F1$ , действующая на заряд со стороны поля $− q$ действует против направления вектора $E$ , сила $F2$ , действующая на заряд $+ q$ со стороны поля действует вдоль вектора $E$ . В первом случае заряды притягиваются с силой $F$ , а во втором $F ′$ .

Рассмотрим первый случай.
Силы $F1$ и $F2$ равны:

F1 = qE, F2 = qE.

А сила взаимодействия зарядов:

2 F = kq2-. l0

Здесь $k$ – постоянная Кулона, $l 0$ – длина недеформированной пружины.
Запишем второй закон Ньютона для одной из частиц:

F⃗1 + ⃗F = m ⃗a,

где $a$ – ускорение частицы.
Так как стержень и бусинки находятся в равновесии, то $a= 0$ .
Спроецируем на горизонтальную ось:

2 qE = kq2. (1) l0

Во втором случае расстояние между частицами уменьшается в 2 раза и становится равным $l0∕2$ , тогда сила Кулона становится равна:

′ kq2 4kq2 F = (l0∕2)2-= -l20-.

Также во втором случае действует сила упругости $Fy$ , которая равна

( ) Fy = KΔx = K l0− l0 = Kl0, 2 2

где $K$ – коэффициент жёсткости пружины, $Δx$ – сжатие пружины.
Запишем второй закон для одной из частицы Ньютона:

⃗F1+ ⃗F′+ ⃗Fy = m ⃗a′,

где $′ a$ – ускорение частицы.
Так как стержень и бусинки находятся в равновесии, то $a′ = 0$ .
Спроецируем на горизонтальную ось:

4kq2 Kl0 qE + -l2--− -2-= 0. 0

С учетом (1)

∘ ----- kq2 4kq2 Kl0 310kq2 l20 + l20 = 2 ⇒ l0 = K

Тогда

∘ ------- E = kq = ∘--kq----⇒ K = 100qE3 ≈ 100 Н/м l20 3100k2q4- k K2

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон Кулона, записана формула силы электрической, второй закон Ньютона, формула силы упругости. Указание того, что ускорение равно нулю);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 12#24196

Маленький заряженный шарик массой 50 г, имеющий заряд 1 мкКл, движется с высоты 0,5 м по наклонной плоскости с углом наклона 30 $∘.$ В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд 7,4 мкКл. Какова скорость шарика у основания наклонной плоскости, если его начальная скорость равна нулю? Трением пренебречь.

Источники: Основная волна 2003

Показать ответ и решение

Сделаем рисунок.

Начальная энергия взаимодействия шариков равна:

kqq W1 = -h12, (1)

где $q1$ – заряд первого шарика, $q2$ – заряд второго шарика, $h$ – начальная высота.
Также первый шарик на высоте $h$ имел потенциальную энергию, равную:

E =mgh, (2 n

где $m$ – масса шарика.
Конечная энергия взаимодействия шариков равна:

kq1q2- W2 = l , (3)

где $h l = tgα$ , $α= 30∘$ .
В положении II шарик имеет кинетическую энергию:

2 Ek = mv--, (4) 2

где $v$ – искомая величина.
Запишем закон сохранения энергии:

W1 +En = W2 + Ek (5)

Объединим (1) – (5):

kq1q2- kq1q2tg-α mv2- h + mgh = h + 2 .

Отсюда

∘ ------------------ ∘ ----------------9-----−6-------−6-------- v = 2gh+ 2kq1q2(1 − tgα)= 2⋅10⋅0,5+ 2⋅9-⋅10-⋅1-⋅10---⋅7,4⋅10--(1− √1-)= 3,5 м/с mh 0,05 ⋅0,5 3

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения механической энергии с учетом энергии взаимодействия электрических зарядов, формулы кинетической энергии точки, потенциальной энергии тела в однородном поле тяжести и потенциальной энергии взаимодействия точечных зарядов);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 13#39129

В однородном электрическом поле с напряжённостью $E = 18$ В/м находятся два точечных заряда: $Q = − 1$ нКл и $q = +5$ нКл с массами $M = 5$ г и $m = 10$ г соответственно (см. рисунок). На каком расстоянии $d$ друг от друга находятся заряды, если их ускорения совпадают по величине и направлению? Сделайте рисунок с указанием всех сил, действующих на заряды. Силой тяжести пренебречь.

Источники: Демоверсия 2023

Показать ответ и решение

Направим ось Ox по напряжённости электрического поля $⃗ E$ .

На заряд $q$ действует две силы: электрическая

F1 = qE,

и сила Кулона:

kq|Q| F ′ = F =-d2-.

На заряд $Q$ также действует две силы:

F2 = |Q |E,

и сила Кулона:

F′′ = F = kq|Q|. d2

Направление сил указано на рисунке.

Второй закон Ньютона запишется в виде:

F⃗′+ ⃗F1 = m⃗a

⃗F′′+F⃗2 = M⃗a,

где $a$ – ускорение тел.
Спроецируем на ось $Ox$ :

F1− F = ma

F − F2 = Ma

Тогда

F1−-F- F-−-F2 m = M .

Тогда с учётом выражений для сил можно выразить $d$

∘ ------------- ∘ ----9-----−9--------−-9----------- d= kq|Q|(m-+-M-)= 9-⋅10-⋅5-⋅10---⋅|−-1|⋅10-(0,01+-0,005)= 1 м E (m |Q |+Mq ) 18(0,01⋅|− 1|⋅10−9+ 0,005 ⋅5⋅10−9)

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон Кулона, второй закон Ньютона, формула для связи напряжённости электрического поля с силой, действующей на заряд);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 14#40403

Электрон со скоростью $6 v = 5⋅10$ м/с влетает в пространство между пластинами плоского конденсатора, между которыми поддерживается разность потенциалов $U = 500$ В (см. рисунок). Каково максимальное удаление электрона $h$ от нижней пластины конденсатора? Отношение заряда электрона к его массе равно $γ = −1,76⋅1011$ Кл/кг. Угол падения электрона $α = 60∘$ . Расстояние между пластинами конденсатора равно $d= 5$ см.

Показать ответ и решение

Напряженность поля внутри пластин конденсатора равна:

U E = d.

Внутри пластин на заряд действует тормозящая электрическая сила, направленная перпендикулярно пластинам конденсатора:

F = eE = eU-. d

Максимальное удаление от нижней пластины конденсатора будет при $v = 0 x$ (см. рис.)

При влете электрона в пластину его кинетическая энергия равна:

mv2 m(v2+ v2) E0 = -2--= ---x2---y.

На максимальном удалении $h$ от нижней пластины кинетическая энергия равна:

2 E1 = mv-y. 2

При этом $v = vcosα x$ , $v = vsinα y$ . Запишем закон об изменении кинетической энергии:

E1− E2 = A,

где $A = Fh$ – работа поля.
Тогда

2 2 2 2 2 mvy-− m(vx+-vy)= eUh.⇔ − mv-cosα-= eU-h. 2 2 d 2 d

Отсюда

2 h = − m ⋅ v2cosα⋅d= − v2cos2αd-= − 25⋅1012 (м/с)⋅0,25⋅0,05 м-= 0,0018 м q 2U 2Uγ 2⋅500 В ⋅(− 1,76⋅1011) Кл/кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: формула силы электрической, формула связи напряженности и напряжения, формула кинетической энергии, закон изменения кинетической энергии, формула работы силы);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 15#40404

Маленький шарик с зарядом $−7 q =4 ⋅10$ Кл и массой 3 г, подвешенный на невесомой нити с коэффициентом упругости 100 Н/м, находится между вертикальными пластинами плоского воздушного конденсатора. Расстояние между обкладками конденсатора 5 см. Какова разность потенциалов между обкладками конденсатора, если удлинение нити 0,5 мм?

Показать ответ и решение

На шарик действует сила упругости $Fупр$ со стороны нити, сила тяжести $mg$ и сила действия электрического поля $Fэл$ . Расставим эти силы:

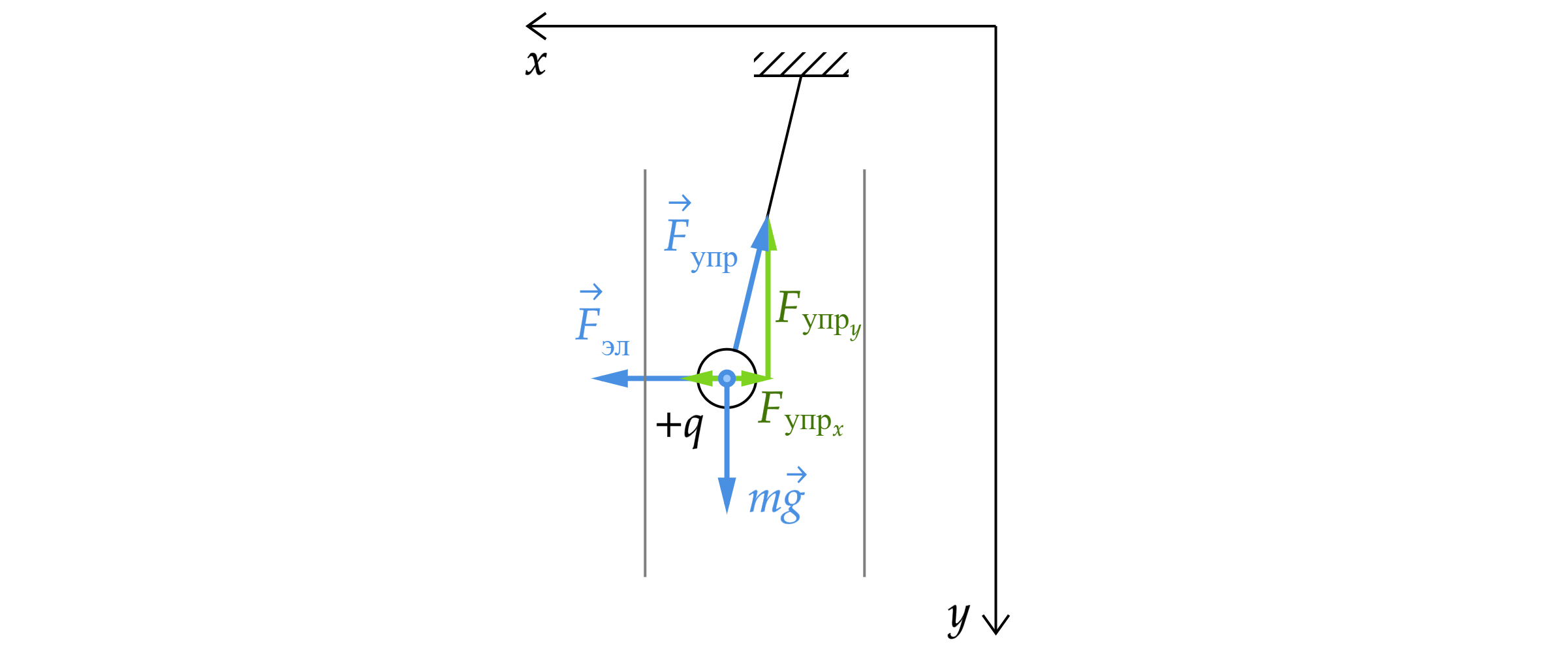
Запишем второй закон Ньютона:

F⃗упр +m ⃗g+ ⃗Fэл = m⃗a,

где $m$ – масса шарика, $a$ – его ускорение.
Так как тело покоится, то $a = 0$ . Спроецируем второй закон Ньютона на оси $x$ :

Fупр. х =Fэл

и $y$ :

Fупр. у = mg.

Электрическая сила равна:

Fэл =qE = qU-, d

где $E$ – напряженность между пластинами, $U$ – разность потенциалов между пластинами, $d$ – расстояние между пластинами.
Сила упругости же равна:

Fупр = kΔl,

где $k$ – жёсткость нити, $Δl$ – удлинение нити.
Из теоремы Пифагора:

( )2 F2упр = F2упр. х +Fу2пр. у ⇔ (kΔl)2 = qU + (mg)2 d

Отсюда:

d∘ (kΔl)2−-(mg)2 0,05 м∘ (100 Н/м-⋅0,0005-м)2-− (0,003 кг⋅10 Н/-кг)2 U = -------q-------= -----------------4⋅10−7-Кл----------------- =5000 В

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: второй закон Ньютона, формула силы электрической, формула связи напряженности и напряжения, формула силы упругости, формула нахождения резульирующей силы упругости);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 16#40711

В центре сферы радиусом $R$ находится точечный заряд $Q > 0$ . По сфере распределён равномерно заряд $− 4Q < 0$ . Найти напряжённости $E1$ и $E2$ на расстояниях $R∕2$ и $2R$ от центра сферы.

Показать ответ и решение

В любой точке напряжённость равна векторной сумме напряжённостей полей, созданных зарядами $Q$ и $− 4Q$ :

E⃗= ⃗EQ + ⃗E−4Q.

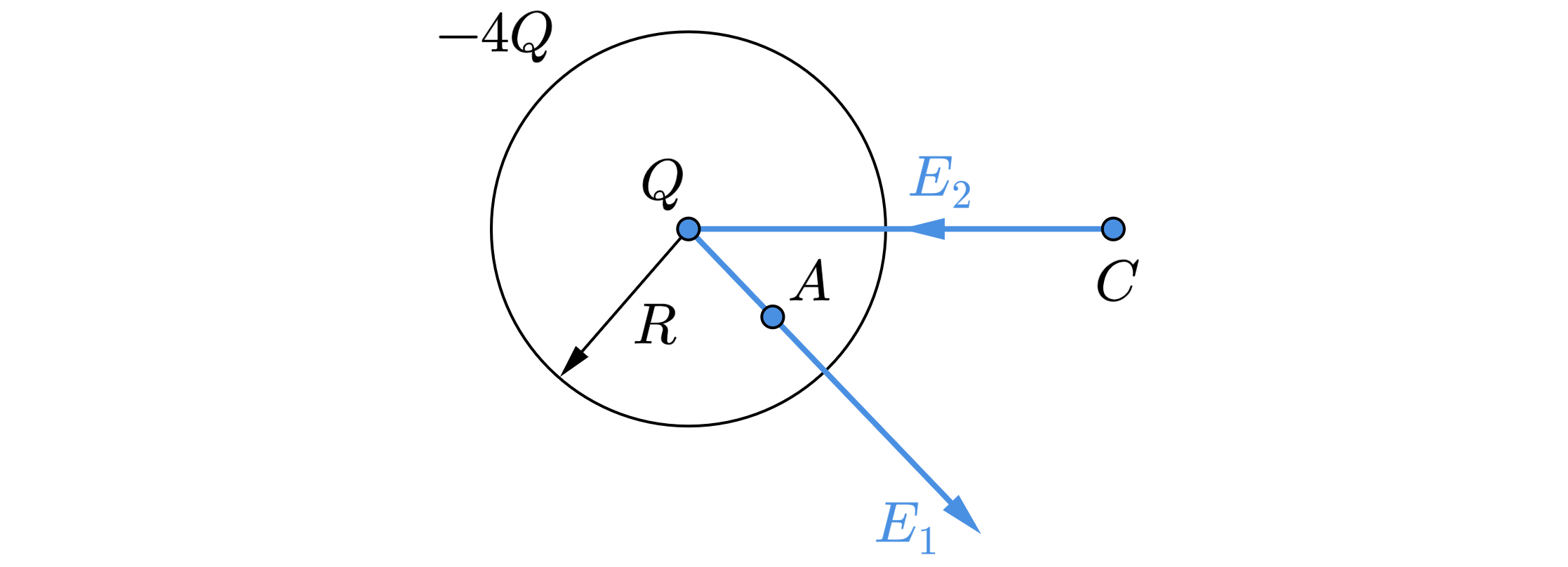
Это векторное равенство можно записать в проекциях на ось $x$ , проведённую из центра сферы через исследуемую точку:

Ex = EQx+ E−4Qx.

Напряженность поля в точке, находящейся на расстоянии $r$ от точечного заряда равна:

E = k-q2, r

где $q$ – заряд.
Напряженность внутри сферы равна нулю, тогда на расстоянии $R∕2$ напряженность создаёт только точечный заряд:

kQ Q E1Q = (R-∕2)2-=4k R2-

Напряженность поля точечного заряда направлена к заряду в случае отрицательного заряда и от заряда в случае положительного заряда, значит, внутри сферы напряженность направлена к поверхности сферы.

Напряженность сферы на расстоянии $r >R$ от центра сферы описывается уравнением:

E(r)= k-⋅(−24Q-) R

на расстоянии $2R$

E2(2R) = k⋅(−4Q)-=− k Q- (2R)2 R2

А для точечного заряда:

kQ E2Q = 4R2.

Напряженность поля направлена к заряду в случае отрицательного заряда и от заряда в случае положительного заряда, так как заряд сферы по модулю больше, то напряженность также направлена к поверхности сферы, а её модуль равен

Q-- -kQ- 3kQ- E2 =k R2 − 4R2 = 4R2

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: принцип суперпозиции электрических полей, формула напряженности точечного электрического заряда, описаны направления напряженности да положительного и отрицательного заряда);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 17#40712

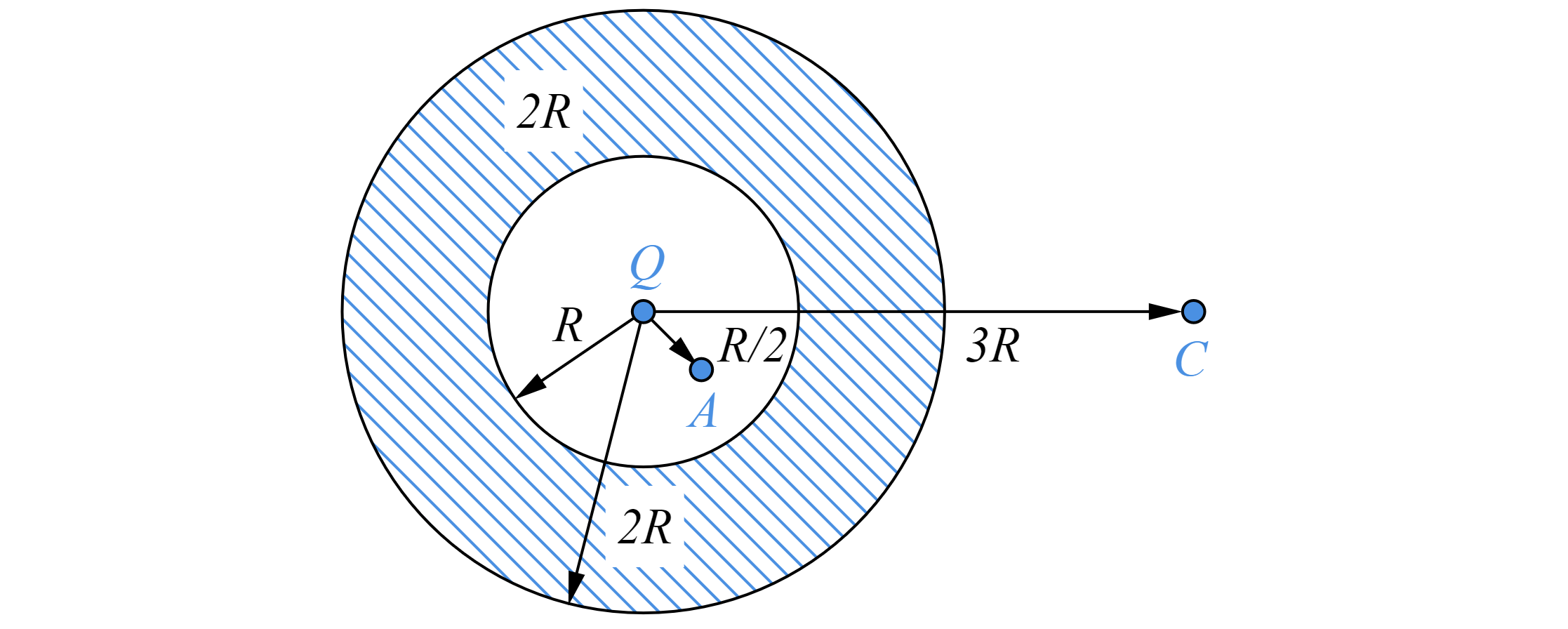
Два одинаковых отрицательных точечных заряда по 100 нКл массой 0,3 г каждый движутся по окружности радиусом 10 см вокруг положительного заряда 100 нКл. При этом отрицательные заряды находятся на концах одного диаметра. Найдите угловую скорость вращения зарядов.

Показать ответ и решение

Заряды взаимодействую друг с другом, при этом на каждый из зарядов действует как сила отталкивания к отрицательному заряду:

q2 F − = k(2R)2,

где $q$ – заряд, $R$ – радиус обращения.
Так и сила притяжения к положительному заряду:

qQ- F+ = kR2 ,

где $Q$ – положительный заряд в центре.
Изобразим силы, действующие на один из зарядов, с учётом вше описанных сил.

Запишем второй закон Ньютона для заряда:

⃗F− +F⃗+ = m⃗a,

где $m$ – масса заряда, $a$ – центростремительное ускорение.
Центростремительное ускорение равно:

a = ω2R,

где $ω$ – угловая скорость вращения зарядов.
Спроецируем второй закон Ньютона на ось, проходящую через отрицательный заряд к положительному заряду.

− F + F = mω2R − +

или

2 kqQ2-− kq2 = m ω2R R 4R

Так как $Q = q$ , то

3k q2-= mω2R. 4 R2

Отсюда искомая величина:

∘ ---- −9 ∘ --------9------- ω = -q- -3k = 100⋅10--К-л --3⋅9⋅−130-м/Ф----= 15 рад/с 2R mR 2⋅0,1 м 0,3 ⋅10 кг⋅0,1 м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: формула силы Кулона, второй закон Ньютона, формула центростремительного ускорения);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 18#40713

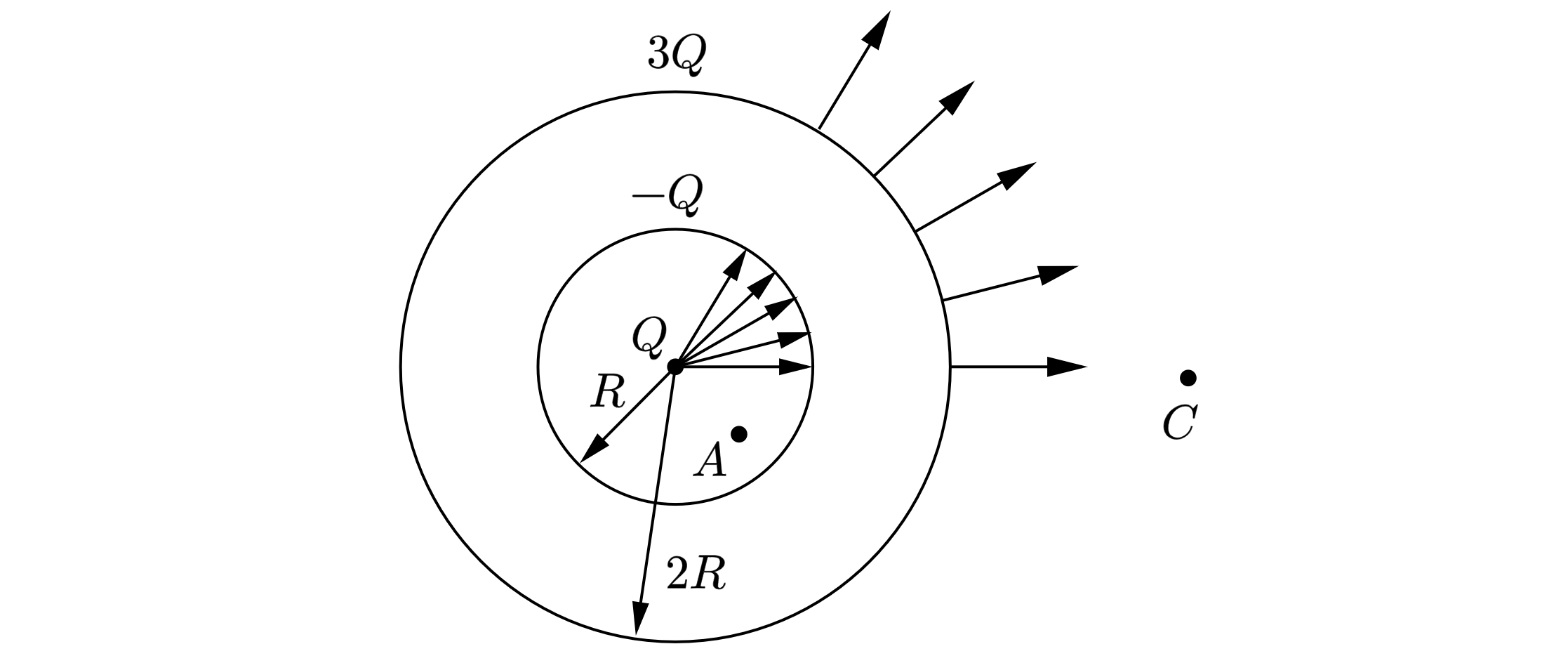
Проводящий полый шар (см. рис.) с радиусами сферических поверхностей $R$ и $2R$ имеет заряд $2Q$ ( $Q > 0$ ). В центре шара находится точечный заряд $Q$ . Найти напряженность и потенциал в точках $A$ и $C$ на расстояниях $R ∕2$ и $3R$ от центра шара. Найти потенциал полого шара.

Показать ответ и решение

Заряд $2Q$ распределится по внутренней и внешней сферическим поверхностям, так как материал, из которого сделан шар, является проводником. В промежутке между $R$ и $2R$ напряженность поля равна нулю, так как шар проводник, а напряженность в проводнике равна нулю. Если силовые линии "начинаются"на $+ Q$ , то они должны "заканчиваться"на $− Q$ . То есть заряд внутренней поверхности шара равен $q1 =− Q$ . По закону сохранения заряда, заряд на внешней поверхности шара равен:

q1 +q2 = 2Q ⇒ q2 = 2Q − q1 = 2Q − (−Q) =3Q.

Изобразим силовые линии и заряды поверхностей шара.

Для точек $A$ и $C$ напряженности можно найти по принципу суперпозиции. Направим ось $x$ из центра шара в исследуемую точку (для точек $A$ и $C$ оси $x$ различны). По принципу суперпозиции напряженность результирующего поля равна сумме напряженностей. Пусть напряженность, создаваемая точечных зарядом равна $E1$ , внутренней поверхность шара $E2$ , внешней поверхностью шара $E3$ . По принципу суперпозиции для точки $A$ :

--Q--- Q-- EAx =E1x +E2x +E3x = k(R∕2)2 + 0+ 0= 4kR2 > 0.

Для точки $C$ :

ECx = E1x+ E2x+ E3x = k-Q-2 + k-−-Q2 + k-3Q-2 = 1k Q2-> 0 (3R) (3R) (3R) 3 R

Проекции получились положительные, значит, напряженности направлен от центра шара (см. рисунок выше). Кроме того напряженности направлены от положительного заряда к отрицательному.

Потенциал также найдём по принципу суперпозиции. для точки $A$ :

Q −Q 3Q 5 Q φA = φ1 +φ2 + φ3 = kR∕2-+ kR-+ k2R-= 2kR

Аналогично для токи $C$ :

Q −Q 3Q Q φC =φ1 + φ2+ φ3 = k3R-+ k3R-+ k3R-= kR

Потенциал шара можно найти, как потенциал наружной поверхности сферы, то есть, по принципу суперпозиции

φ= φ1 +φ2 +φ3 = k Q-+k −Q-+ k3Q-= 3kQ- 2R 2R 2R 2 R

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: закон сохранения электрического заряда, принцип суперпозиции электрических полей, формула напряженности электрического поля точечного заряда, формула потенциала точечного заряда, принцип суперпозиции потенциалов, сказано, в каком случае напряженность равна нулю);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

ПрПравильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 19#47584

Точки $A,B,C$ и $D$ расположены на прямой и разделены равными промежутками $L$ (см. рисунок). В точке $A$ помещен заряд $q1 = 8⋅10−12$ Кл, в точке $B −$ заряд $q2 = −5 ⋅10−12$ Кл. Какой заряд $q3$ надо поместить в точку $D$ , чтобы напряженность поля в точке $C$ была равна нулю?

Показать ответ и решение

Напряженность поля точечного заряда определяется формулой:

k|q| E = -r2 ,

где $r$ – расстояние от точечного заряда, $|q|$ – модуль заряда.
Вектор напряженности положительного заряда направлена от заряда, а вектор напряженности отрицательного к заряду Напряженность в точке $C$ можно найти по принципу суперпозиции, как сумму напряженностей всех других зарядов.

⃗ ⃗ ⃗ ⃗ EC = EA + EB +ED.

Пусть вектора напряженностей направлены так, как показано на рисунке (то есть заряд в точке $D$ положителен).

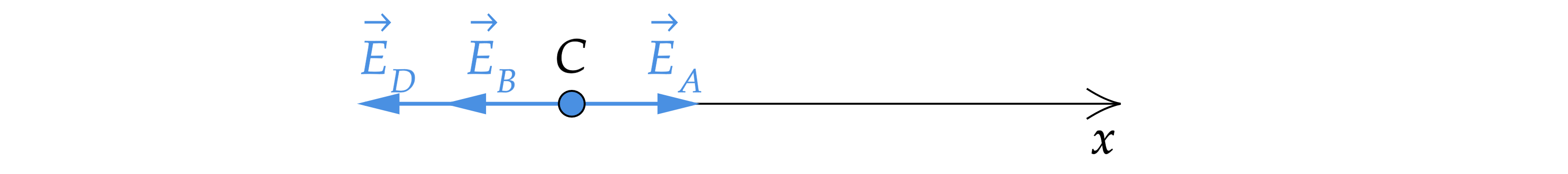
Спроецируем уравнение принципа суперпозиции на ось $x$ , с учётом, что напряженность в точке $C$ равна нулю:

EA =ED + EB.

Распишем напряженности по формулам:

k|q1| EA = (2L-)2,

EB = k|q2|, L2

k|q3| ED = L2 .

Подставим в уравнение

k|q1|- k|q3| k|q2| (2L)2 = L2 + L2

Отсюда можно выразить искомый заряд $q3$ :

−12 |q3|= |q1|− |q2|= |8-⋅10---К-л− 5⋅10−12 К л|=|− 3⋅10−12 К л| 4 4

Значение заряда под модулем отрицательное, значит исходное направление $ED$ выбрано неверно, потому что заряд должен быть отрицательным, ответ:

−12 − 3⋅10 Кл

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: формула напряженности точечного электрического заряда, принцип суперпозиции электрических полей);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 20#47585

Четыре одинаковых заряда $q$ расположены на плоскости в вершинах квадрата со стороной $L$ и удерживаются в равновесии связывающими их попарно нитями (см. рис.). Сила отталкивания соседних зарядов равна $F0 = 20⋅10−3$ Н. Чему равно натяжение каждой из нитей?

Показать ответ и решение

Расставим силы, действующие на заряды

где $Fij$ – сила отталкивания $i$ заряда от $j$ .

При этом силы $F41$ , $F32$ , $F14$ , $F32$ направлены вдоль диагоналей.

Сила взаимодействия зарядов равна

F = kq2. r2

Здесь $k$ – постоянная Кулона, $r$ – расстояние между зарядами.
Расстояние между зарядами равно: $r12 =r24 = r43 = r31 = l$ , $√ 2---2 √- r14 = r23 = l +l = l 2.$ Тогда с учётом условия:

kq2 F21 = F31 = F42 = F12 = F34 = F24 = F13 = F43 =-l2-= F0. (1)

2 F41 = F32 = F14 = F32 = kq2 = F0. (2) 2l 2

Из (1) и (2) следует, что сила натяжения каждой из нитей будет равна, значит, нам необходимо найти всего одну из них. Рассмотрим заряд 1. Запишем для него второй закон Ньютона:

⃗F31+ ⃗F21+ ⃗F41 +T⃗12+ ⃗T13 = ma⃗1,

где $m$ – масса заряда, $a1$ – его ускорение.
Найдем силу натяжения $T12$ , для этого спроецируем второй закон Ньютона на ось $x$ , с учётом что тела покоятся ( $a1 = 0$ )

√ - ( √ -) ( √-) T12 = F21+ F41⋅cos45∘ =F0 + F0⋅-2= F0 1+ --2 = 20⋅10−3 Н⋅ 1+ -2- = 2,7⋅10−2 Н 2 2 4 4

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае: формула силы Кулона, теорема Пифагора, второй закон Ньютона);
II) описаны все вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при
написании физических законов);
III) представлены необходимые математические преобразования и
расчёты, приводящие к правильному числовому ответу
(допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
искомой величины

Правильно записаны все необходимые положения теории,	2
физические законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И (ИЛИ)
В решении лишние записи, не входящие в решение (возможно,
неверные), не отделены от решения (не зачёркнуты; не заключены
в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) преобразования/вычисления не
доведены до конца.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения задачи (или утверждение, лежащее в основе решения),
но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи
(или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

01 Электростатика