.07 Магнитное поле. Сила Лоренца. Сила Ампера
Ошибка.
Попробуйте повторить позже
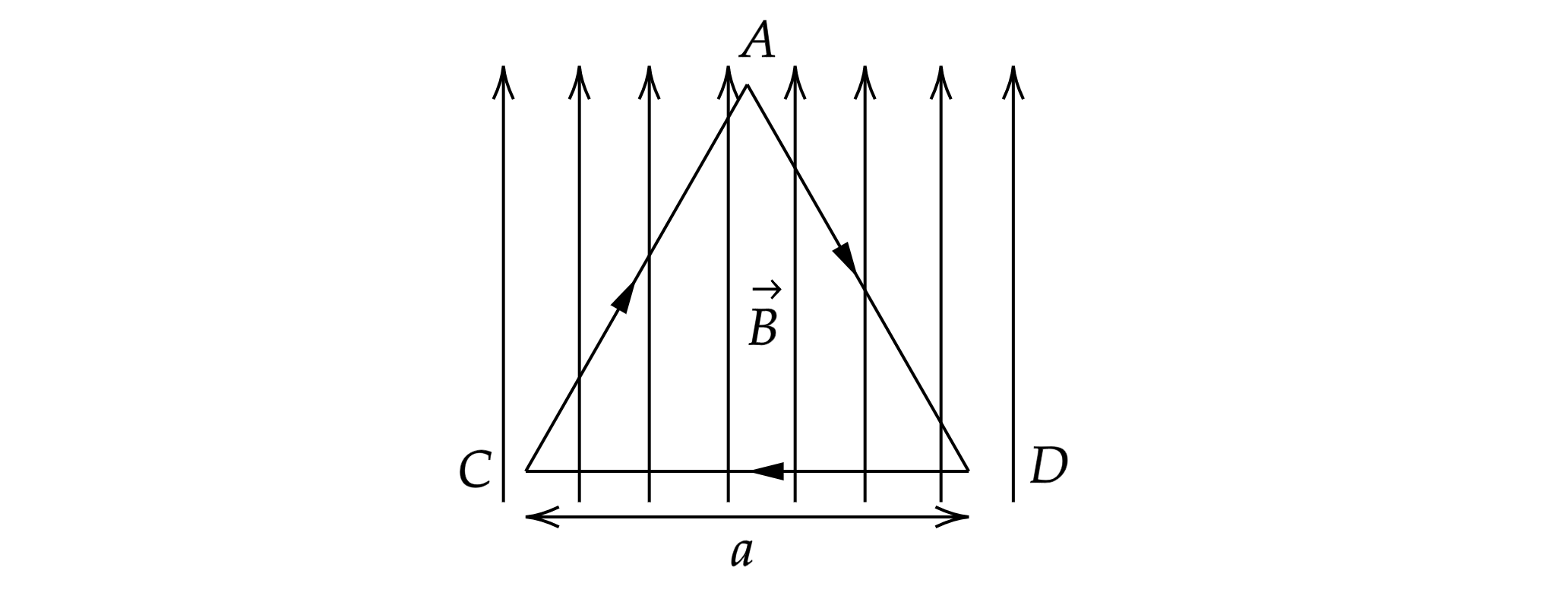
На непроводящей горизонтальной поверхности стола лежит проводящая жесткая рамка из однородной тонкой проволоки, согнутой в
виде равностороннего треугольника со стороной, равной
(см. рис.). Рамка, по которой течет ток
, находится в однородном
горизонтальном магнитном поле, вектор индукции которого
перпендикулярен стороне
. Каким должен быть
модуль индукции магнитного поля, чтобы рамка начала поворачиваться вокруг стороны
, если масса рамки
?
Источники:
На стороны рамки действует сила Ампера. Определим ее направление по правилу Левой руки.
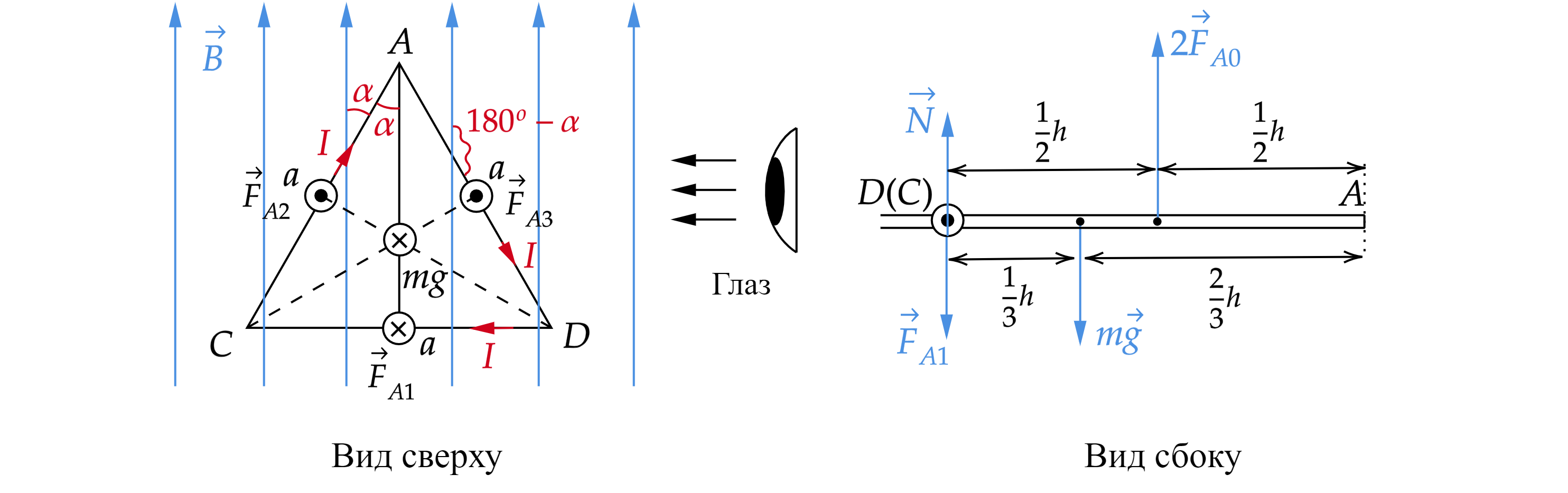
Сила Ампера равна:
где – сила тока через проводник,
– индукция магнитного поля,
– длина проводника,
– угол между направлением
вектора индукции магнитного поля
и направлением тока. Определим значения сил Ампера, действующих на
стороны.
На сторону :
.
На сторону :
,
.
На сторону :
.
Также на рамку действует сила реакции опоры на сторону
и сила тяжести
, направленная вниз (см. рис.) она
приложена в геометрическом центре фигуры, то есть на пересечении медиан треугольника.
Для того чтобы рамка начала поворачиваться вокруг оси , вращательный момент сил, действующих на рамку и
направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Запишем правило моментов
относительно оси
:
Моменты сил и
равны нулю, так как их плечи равны нулю (на рисунке
). Тогда:
| Критерии оценивания выполнения задачи | Баллы |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае: по правилу левой руки определено направление сил Ампера, формула силы Ампера, правило моментов. Отдельно записана формула момента силы); | |
| II) описаны все вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений, используемых в условии | |
| задачи, и стандартных обозначений величин, используемых при | |
| написании физических законов); | |
| III) представлены необходимые математические преобразования и | |
| расчёты, приводящие к правильному числовому ответу | |
| (допускается решение «по частям» с промежуточными | |
| вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| искомой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| физические законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И (ИЛИ)
| |
| В решении лишние записи, не входящие в решение (возможно, | |
| неверные), не отделены от решения (не зачёркнуты; не заключены | |
| в скобки, рамку и т.п.). | |
|
И (ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и (или) преобразования/вычисления не | |
| доведены до конца. | |
|
И (ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| задачи, без каких-либо преобразований с их использованием, | |
| направленных на решение задачи, и ответа. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения задачи (или утверждение, лежащее в основе решения), | |
| но присутствуют логически верные преобразования с имеющимися | |
| формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения задачи | |
| (или в утверждении, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования с | |
| имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




